Практическая работа №3 Изучение структуры кристалла методом Дебая

Цель работы – ознакомление с рентгеновским методом исследования структуры поликристаллических веществ. Индицирование дебаеграммы вещества с кубической решеткой.

Одним из наиболее широко распространенных методов исследования структуры поликристаллических веществ является метод Дебая–Шеррера. Типичная дебаеграмма, полученная в результате дифракции рентгеновских лучей в кристалле, представлена рядом колец (рис. 3. 1).

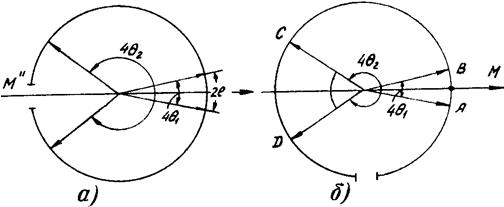
Рис. 3.1. Геометрия съемки в дебаевской камере.

Обычно съемку осуществляют в цилиндрических камерах типа РКД (камера для рентгеноструктурного анализа по методу Дебая). Рентгеновская пленка в ней располагается по внутренней цилиндрической поверхности камеры. При съемке образца в цилиндрической кассете рентгенопленку располагают либо так, чтобы ее концы сходились у входного (для первичного пучка лучей) отверстия камеры М^// (рис. 3.1,а). Это симметричная прямая съемка. Либо концы рентгенопленки сходятся у одного из концов диаметра, перпендикулярного лучу, как показано на рис. 3.1,б. Это асимметричная съемка. При первом способе съемки получают симметричную рентгенограмму (рис. 3.2,б), при втором – асимметричную (рис. 3.2,а).

Расстояния между средними точками колец рентгенограмм пропорциональны соответствующим углам скольжения (рис. 3.1). Действительно, дуга окружности длиной АВ=2 l связана с измеренным в радианах углом при вершине конуса 4q соотношением

4q_рад=2 l /R; q_рад= l /2R, (3.1)

где R – радиус цилиндрической рентгенопленки.

При угле q, измеренном в градусах

q°= × 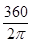=57,3 (3.2)

Если диаметр цилиндрической кассеты 2R взять равным 57,3 мм, то приближенно получим

q » l мм (3.3)

Таким образом, выраженный в градусах угол q будет равен половине расстояния между симметричными линиями рентгенограммы в мм.

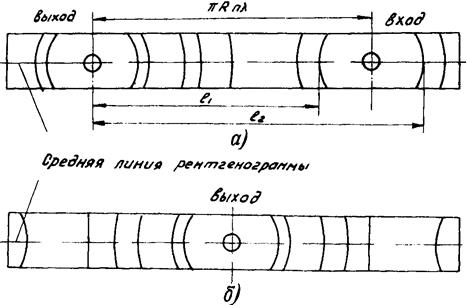
Рис. 3.2.Схема асимметричной (а) и симметричной (б) рентгенограммы.

При обоих способах съемки, симметричной и асимметричной, для расчета q требуется промерить расстояние l от выхода рентгеновского пучка (рис. 3.1) до соответствующего кольца рентгенограммы. По ассиметричному снимку можно, кроме того, точно рассчитать радиус свернутой фотопленки и, следовательно, с большой точностью вычислить для каждой интерференционной линии угол скольжения

q = × l (3.4)

Очевидно, что расстояние по окружности между осями симметрии, расположенными у входного и выходного отверстий равно pR (рис. 3.1). Тогда для любой пары линий, например C и D, относящихся к одному и тому же конусу дифракции у входного отверстия

pR=(l₁+l₂)/2, (3.5)

где l₁ и l₂ – расстояние этих линий от оси симметрии М у выходного отверстия. При подсчете радиуса пленки берут несколько таких пар линий у входа, рассчитывают по каждой паре pR и определяют затем среднее значение этой величины.

При симметричном способе съемки рассчитать радиус свернутой фотопленки по снимку невозможно и его либо приравнивают к радиусу камеры, либо ведут съемку с эталоном.

Каждая линия на рентгенограмме получается в результате отражения рентгеновских лучей от какой-либо системы параллельных атомных плоскостей (HKL), так что индексы линий HKL на рентгенограмме совпадают с индексами отражающих плоскостей.

При съемке поликристаллического неподвижного образца в монохроматическом излучении положение линий на пленке-рентгенограмме определяется углом скольжения q. Определив угол скольжения q, можно сопоставить данную линию рентгенограммы системе плоскостей (HKL), или найти ее индексы интерференции. Например, для кубической решетки зависимость между индексами интерференций линии HKL и углом скольжения q определяется из сопоставления двух уравнений:

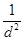= и l=2d_HKL× sinq

откуда sinq= 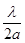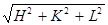, (3.6)

где a – период решетки, d – межплоскостное расстояние системы плоскостей (HKL), HKL – индексы интерференции линий.

Из уравнения (3.6) следует, что чем больше сумма квадратов индексов (H²+K²+L²) линий, тем больше угол отражения q. Следовательно, на рентгенограмме интерференционные линии будут располагаться в порядке возрастания суммы квадратов индексов отражающих плоскостей. Исходя из этого, можно составить таблицу, показывающую очередность расположения интерференционных линий на рентгенограмме поликристалла (табл. 3.1).

Пользуясь соотношением (3.6), легко также установить максимально возможное число интерференционных линий на рентгенограмме. В силу того, что правая часть уравнения (3.6) не может быть больше 1 – на рентгенограмме должны появиться лишь те линии, для которых

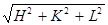£ (3.7)

Из этого неравенства вытекает, что общее количество линий на рентгенограмме определяется длиной волны рентгеновских лучей, а также размерами и формой элементарной ячейки. Чем жестче излучение (меньше l), тем больше линий появится на снимке.

Таблица 3.1

Последовательность расположения линий на дебаеграмме

Например, в кубической решетке при a = 2Å и l = 1,54Å имеем 2a/l=4/1,54»2,59 и H²+K²+L²£2,59²£7. Т.е., согласно табл. 1, максимально может появиться 6 линий, а с учетом погасаний – еще меньше. Последнее связано с тем, что в природе не существует структур с примитивной ячейкой. Реальные кристаллы имеют элементарные ячейки, в которых атомы располагаются не только по вершинам, но и внутри, а также на боковых гранях ячейки. В этих условиях относительная интенсивность рентгеновских лучей, отраженных от какой-либо плоскости (HKL), будет определяться структурной амплитудой F. Некоторые линии, для которых F=0, на рентгенограммах исчезают.

Одно из важнейших применений рентгеноструктурного анализа – это фазовый анализ вещества. Каждое вещество в определенной кристаллической форме имеет вполне определенный набор различных межплоскостных расстояний d. Эта совокупность межплоскостных расстояний является своего рода паспортом данного вещества, по которому можно определить его, пользуясь справочными таблицами. Если исследуемое вещество состоит из двух или более фаз, то рентгенограммы каждой из них накладываются, и для расшифровки такой сложной картины необходимо знать химический состав исследуемого образца. Для однофазного же вещества по рентгенограмме можно, рассчитав набор всех d, определить кристаллическую структуру и химический состав.

Расчет сводится к определению всевозможных межплоскостных расстояний, которые соответствуют данному поликристаллическому веществу, и к сопоставлению их с табличными значениями d для различных веществ и их структурных модификаций.

Схема расчета следующая: замеряют расстояние l (или 2 l, когда имеется такая возможность) от выхода рентгеновского пучка до всех колец рентгенограммы (рис. 3.2,а). Номера колец возрастают в порядке увеличения угла скольжения. Рассчитывают радиус фотопленки R, поскольку съемка асимметричная. Для этого промеряют l для одной или нескольких пар колец, соответствующих большим углам q и вычисляют R по формуле pR=(l _n+ l _n+1)/2. (В случае прямой симметричной съемки R принимают равным радиусу камеры). Зная l и R, находят соответствующий каждой линии угол скольжения q, из соотношения q°= l. При точном определении угла отражения в измеренные значения необходимо внести поправку на поглощение рентгеновских лучей в образце. Отделяют линии b-излучения от линий a-излучения.

Рассмотрим этот вопрос несколько подробнее. Ранее мы считали, что используем монохроматическое излучение. На самом деле рентгеновская трубка дает линейчатый характеристический спектр, включающий ряд линий различных длин волн. Из них все длинноволновое излучение поглощается воздухом и окном рентгеновской трубки, кроме наиболее интенсивных линий К-серии: K_a и K_b. Длина волны их различна (l_Ka>l_Kb), поэтому одна и та же атомная плоскость (HKL) кристалла отражает эти лучи под разными углами и дает на рентгенограмме не одну, а две линии. Это усложняет расчет рентгенограммы.

Снять линии, обусловленные b-излучением можно, применяя фильтры, однако это не всегда желательно, т.к. увеличивает экспозицию примерно в 1,5 раза. Поэтому на практике часто снимают рентгенограммы без фильтра, а из расчета исключают b-линии.

В связи с тем, что длина волны b-излучения всегда несколько меньше, чем a-излучения, на рентгенограмме каждой линии HKL-b соответствует линия HKL-a, причем последняя должна быть сдвинута в сторону больших углов q. Кроме того линии HKL-a в 6–8 раз более интенсивны, чем HKL-b. Это приводит к тому, что для слабых a-линий b-кольца могут вовсе не наблюдаться, а в том случае, если отражение HKL-a интенсивно, то соответствующее ей b-кольцо, расположенное ближе к выходу, выглядит, как слабое.

И, наконец, для этих пар линий должно выполняться соотношение

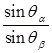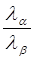= , (3.8)

где l_a и l_b – известные длины волн того излучения, на котором снимается рентгенограмма.

Пользуясь этими признаками, и исключают все линии b-излучения.

Отфильтровав все b-линии, вычисляют межплоскостное расстояние для каждой линии a-излучения. Оно согласно формуле Вульфа–Брегга равно: d= 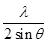. По набору d для данного вещества и справочным таблицам определяют вещество, например, кристалл ZnSe кубической модификации и т.п.

Если конечной целью расчета дебаеграммы является определение параметров элементарной ячейки исследуемых веществ, то, помимо межплоскостных расстояний, необходимо установить индексы каждой интерференционной линии на рентгенограмме. Эта задача решается сравнительно просто только для кристаллов кубической симметрии. Индицирование рентгенограмм поликристаллических веществ с низкой симметрией представляет большую трудность, а иногда невозможно.

Для кубических кристаллов существует следующая зависимость между индексами отражающей плоскости (HKL) и межплоскостным расстоянием d:

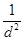= . (3.9)

Индицирование рентгенограмм кубических кристаллов осуществляем, используя известное уже положение, что линии на рентгенограмме поликристалла располагаются в порядке возрастания суммы H²+K²+L². Поэтому для кристаллов с примитивной ячейкой первой линией была бы 100, для которой H²+K²+L² = 1 (эквивалентные плоскости дадут ту же линию, поэтому их не указываем). Следующие по порядку линии будут иметь индексы, соответствующие последующим значениям H²+K²+L² согласно табл. 3.1.

Для объемноцентрированной ячейки не должны наблюдаться линии, у котороых H+K+L=2n+1, а для гранецентрированной ячейки не будет на рентгенограмме линий с индексами разной четности.

Из табл. 1 следует, таким образом, что если

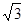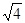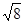: : ...= : : и т.д. (3.10)

то ячейка исследуемого вещества гранецентрированная и первая линия имеет индексы 111, вторая 200, третья 220 и т.д.

Если ячейка объемноцентрированная, ряд будет другой и

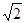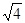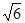: : = : : и т.д. (3.11)

Тогда первая линия на рентгенограмме соответствует 110, вторая 200, третья 211 и т.д.

Используя этот факт, мы можем по рассчитанному для нашей дебаеграммы набору d, получить ряд : :...: 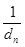, определить тип ячейки и сопоставить кольца дебаеграммы определенным индексам (табл. 1).

Зная индексы, определяем параметр кубической ячейки – a, т.к. из (3.9) а=d_n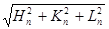

Индицирование рентгенограмм поликристаллических веществ с кубической симметрией можно провести графическим методом. При построении графика, на основе которого производится индицирование, пользуются соотношением (3.6).

Если по оси абсцисс откладывать отношение 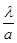, а по оси ординат sin q, то зависимость sinq=f(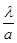) для индексов HKL изображается в виде прямой, проходящей через начало координат. Такой график представлен нарис. 3.3.

Для работы с этим графиком измеряют рентгенограмму и наносят на линейку из плотной бумаги значения sin q, взяв тот же масштаб, который дан на графике. Затем прикладывают линейку к графику параллельно оси ординат так, чтобы ее нулевая точка совпадала с осью абсцисс и перемещают линейку в горизонтальном направлении до тех пор, пока сделанные на ней отметки не совпадут с линиями графика. При этом сразу определяются индексы всех линий, а соответствующая абсцисса равна искомому значению 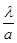. Отсюда найдем a, зная l.

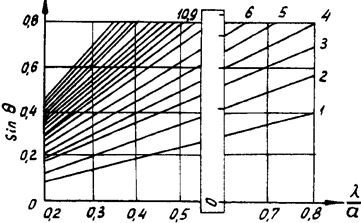
Рис. 3.3. Графическое индицирование дебаеграмм.

По вычисленному параметру a можно рассчитать число атомов, приходящихся на элементарную ячейку. Для этого пользуются соотношением, определяющим плотность кристалла r. Очевидно, что плотность кристалла будет равна общей массе атомов в элементарной ячейке, деленной на объем ячейки. Масса каждого атома равна его атомному весу A, умноженному на массу водородного атома m_H = 1,6725×10^-24 г. Масса N атомов, приходящихся на одну элементарную ячейку, равна N×m_H. Таким образом:

r= 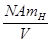(3.12)

Для кубической ячейки V=a³. Тогда

N= . (3.13)

Полученное значение N округляют до целого числа.

Проведенный расчет дает возможность проверить определение типа ячейки кристалла, поскольку в объемноцентрированной ячейке число атомов должно быть равно двум (N=1+1/8:8=2), в гранецентрированной – четырем (N= 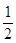×6+ 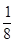×8=4) и т.д.

ЗАДАНИЕ

1. Замерить расстояние l от выхода рентгеновского пучка до всех колец рентгенограммы, результаты занести в таблицу.

2. Рассчитать радиус фотопленки R (съемка асимметричная).

3. Найти соответствующий каждой линии угол скольжения q.

4. Отделить линии b-излучения от линий a-излучения. Для каждой линии a-излучения вычислить соответствующее межплоскостное расстояние.

5. Идентифицировать вещество по набору межплоскостных расстояний.

6. Установить индексы каждой a-линии, определить величину параметра ячейки кристалла.

7. Рассчитать число атомов, приходящихся на элементарную ячейку.