Цель работы – ознакомление с основами электронографии. Индицирование электронограммы образца с аксиальной текстурой.
Наряду с получившими мировое распространение методами рентгенографии для исследования кристаллической структуры используют и другие методы, в частности дифракцию электронов. Исследование кристаллической структуры, в основе которого лежит явление дифракции электронов, получило название электронографии.
Особенности картин, возникающих при дифракции электронов, определяются прежде всего малыми длинами волн электронных пучков и особенностями рассеяния электронов на атомах вещества.
Квантовая механика устанавливает зависимость между длиной волны l эл и импульсом электрона p в виде соотношения Де-Бройля:
 , (6.1)
, (6.1)
где  ; υ – скорость электрона, m – его масса. Если скорости малы, то
; υ – скорость электрона, m – его масса. Если скорости малы, то
 , (6.2)
, (6.2)
Кинетическая энергия электрона с зарядом e определяется ускоряющим напряжением электрического поля U, в котором он движется Wk = eU. Следовательно,
 (6.3)
(6.3)
или из (6.1) длина волны электронного пучка l эл
 (6.4)
(6.4)
Если подставим значения всех известных констант, то получим l эл (в ангстремах при U в вольтах)
 (6.5)
(6.5)
Длины электронных волн, соответствующие напряжениям при которых работают электронографы, лежат в пределах 0,08–0,03 Å. Это почти на два порядка меньше, чем длины волн монохроматического рентгеновского излучения, используемого в структурном анализе.
Другой особенностью электронографических исследований является то, что рассеяние рентгеновских лучей и электронов атомами вещества различно. Как известно, рентгеновские лучи рассеиваются только электронами атома, электроны же рассеиваются электрическими полями электронов атома и атомных ядер. Поскольку в рассеянии электронов участвует практически весь объем атома, для электронов функция атомного рассеяния убывает гораздо резче, чем атомная функция рассеяния рентгеновских лучей. Поэтому на электронограмме не удается получить интерференционных максимумов с высокими индексами интерференции, и интенсивность рефлексов резко снижается с возрастанием угла q.
Благодаря чрезвычайно сильному рассеянию электронов, а также и в силу того, что при получении электронограммы используется почти вся мощность электронного пучка интенсивность дифракционных максимумов электронограммы несравненно выше их интенсивности на рентгенограмме. Вследствие этого электронограмму можно наблюдать на флуоресцирующем экране без дополнительного усиления интенсивности изображения дифракционной картины, а время съемки ее на фотопластинку равно нескольким секундам или долям секунды.
Из-за сильного рассеяния электронов электронография может быть применена для изучения только поверхностных или очень тонких слоев вещества. При получении дифракционной картины “на отражение” глубина проникновения электронов составляет 30–200 Å, хотя сами образцы могут быть массивными.
Малая длина волны электронов (по сравнению с рентгеновскими волнами) приводит к меньшему угловому размытию дифракционных максимумов, что позволяет исследовать весьма мелкодисперсные поликристаллические объекты.
Геометрия возникновения дифракционной картины в случае электронных волн принципиально аналогична случаю рентгеновской дифракции. Особенности возникают из-за малой длины волны электронов. При чрезвычайно малых длинах волн электронных пучков радиус сферы отражения 1/ l эл очень велик – сфера вырождается практически в плоскость (рис. 6.1).Поэтому возможность пересечения ее с узлами обратной решетки много больше. Тепловые колебания решетки дают размытие узлов обратной решетки. Кроме того, пучок электронов из-за колебания напряжения на электронографе может иметь не совсем постоянную l. Это приводит к размытию самой сферы Эвальда и также увеличивает число интерференционных пятен. На электронограмме (рис. 6.2) в этом случае появится множество рефлексов.
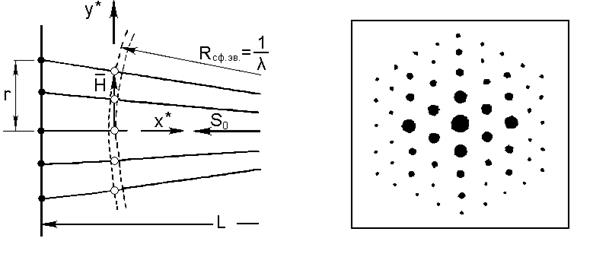
| Рис. 6.1. Проектирование обратной решетки на фотопластинку электронным лучом. | Рис. 6.2. Электронограмма монокристалла. |
Согласно Рис. 6.2 на электронограмме возникает серия пятен, которые в некотором масштабе изображают плоскость обратной решетки, т.е. электронограмма является как бы проекцией слоя обратной решетки, перпендикулярной к лучу. Такая электронограмма называется точечной.
По положению пятен дифракции можно определить межплоскостные расстояния d для системы отражающих плоскостей. Если расстояние между данным пятном электронограммы и следом первичного пучка r (Рис. 6.1), а между образцом и пленкой L, то можно записать
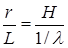 , (6.6)
, (6.6)
если r || H, что допустимо при очень малой кривизне сферы Эвальда. Радиус вектор обратной решетки по величине равен H =1/ d. Поэтому можем переписать выражение (6.6) как
 , (6.7)
, (6.7)
Значение Ll носит название постоянной электронографа.
При взаимодействии электронных волн с поликристаллом получим картину, аналогичную той, которую имеем при съемке поликристаллических порошков дебаевским методом. Вся совокупность дифракционных лучей пойдет по конусам и на плоской фотопленке даст серию концентрических окружностей (Рис. 6.3). Эти окружности сплошные, если размеры кристаллов меньше 10-3 см, или распадаются на отдельные точечные рефлексы при съемке крупнозернистых образцов.

Рис. 6.3. Схема электронограммы поликристалла.
Расчет межплоскостных расстояний осуществляется так же, как и для монокристаллов. Следует отметить, что ввиду малости углов скольжения q для электронных волн погрешность при определении d очень велика.
В поликристаллических образцах очень часто приходится встречаться с преимущественной ориентацией кристаллов. Если кристаллики, составляющие поликристаллический образец (пленку), ориентированы так, что какая-либо кристаллографическая плоскость у всех кристалликов параллельна подложке (поверхности пленки), а вокруг оси, перпендикулярной этой поверхности, кристаллики повернуты произвольно, то возникает так называемая пластинчатая или аксиальная текстура. Аксиальная текстура – наиболее распространенный вид текстуры. Общим для кристалликов является направление нормали к подложке, которое и является осью текстуры. Такие текстуры часто образуются при осаждении из растворов, из пара, при термической возгонке веществ, при электролитическом осаждении на подложку и т.д.

Рис. 6.4. Схема аксиальной текстуры.
Моделью такой аксиальной текстуры является горсть кубиков, брошенная на плоскую поверхность. Данное кристаллическое образование не является, естественно, монокристаллическим, но это уже не абсолютный поликристалл, т.к. в этом случае реализуются не все возможные ориентации кристалликов друг относительно друга. Фактически осталась только одна (вращательная) степень свободы, вокруг оси, перпендикулярной поверхности стола, являющейся осью текстуры. Можно сразу же предсказать, что электронограмма от такого объекта должна отличаться как от точечных электронограмм монокристалла, так и от электронограмм поликристаллов.
Рассмотрим построение дифракционной картины для поликристаллической пленки, в которой ось аксиальной текстуры 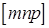 располагается перпендикулярно поверхности пленки и, следовательно, поверхности подложки. В этом случае электронограмма будет иметь ряд характерных особенностей:
располагается перпендикулярно поверхности пленки и, следовательно, поверхности подложки. В этом случае электронограмма будет иметь ряд характерных особенностей:
1. Для идеальной текстуры электронограмма точечная.
2. Точки, на которые распадаются сплошные кольца электронограммы, будут расположены симметрично относительно вертикальной оси электронограммы.
3. На оси электронограммы будут лежать точки, индексы которых определяют ось аксиальной структуры.

Рис. 6.5. Схема электронограммы идеально текстурированной пленки.
При съемке на отражение электронный луч падает на пленку под очень небольшим углом 1–3º (Рис. 6.5.). Тогда угол между лучом и осью текстуры можно считать прямым.
Рассмотрим отражение электронного пучка от одной системы параллельных плоскостей  . Ориентацию таких плоскостей во всем объеме поликристалла можно представить ориентацией их нормалей. Допустим, что N1 – нормаль к плоскости
. Ориентацию таких плоскостей во всем объеме поликристалла можно представить ориентацией их нормалей. Допустим, что N1 – нормаль к плоскости  в одном из кристалликов. Она составляет с осью текстуры
в одном из кристалликов. Она составляет с осью текстуры 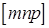 угол φ 1. Остальные кристаллики в текстурированной поликристаллической пленке отличаются по ориентации от первого только поворотом вокруг оси текстуры. При этом поворот кристалликов будет равносилен вращению нормали N1 вокруг той же оси
угол φ 1. Остальные кристаллики в текстурированной поликристаллической пленке отличаются по ориентации от первого только поворотом вокруг оси текстуры. При этом поворот кристалликов будет равносилен вращению нормали N1 вокруг той же оси 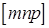 . Поэтому, повороту вокруг оси аксиальной текстуры на разные углы бесчисленного множества кристалликов будет соответствовать конус нормалей с углом при вершине 2 φ 1 (Рис. 6.5.).
. Поэтому, повороту вокруг оси аксиальной текстуры на разные углы бесчисленного множества кристалликов будет соответствовать конус нормалей с углом при вершине 2 φ 1 (Рис. 6.5.).
Рассмотрим, для каких из этих ориентаций условие дифракции выполнимо. Отражение электронных волн от плоскостей  возможно, если последняя наклонена к лучу под углом θ 1, удовлетворяющим условию Вульфа–Брегга, а нормаль N1 составляет с падающим лучом угол (90– θ 1)º. Поскольку угол θ 1 очень мал, то все нормали к отражающим плоскостям должны лежать в плоскости Q, перпендикулярной падающему пучку (Рис. 6.5.).
возможно, если последняя наклонена к лучу под углом θ 1, удовлетворяющим условию Вульфа–Брегга, а нормаль N1 составляет с падающим лучом угол (90– θ 1)º. Поскольку угол θ 1 очень мал, то все нормали к отражающим плоскостям должны лежать в плоскости Q, перпендикулярной падающему пучку (Рис. 6.5.).
Таким образом, дифракция от плоскостей  будет наблюдаться только для тех кристаллов, у которых нормали N лежат одновременно на поверхности конуса нормалей и в плоскости Q. Это соответствует пересечению конуса нормалей с плоскостью Q (Рис. 6.5.). Линии их пересечения позволяют выделить из всех плоскостей
будет наблюдаться только для тех кристаллов, у которых нормали N лежат одновременно на поверхности конуса нормалей и в плоскости Q. Это соответствует пересечению конуса нормалей с плоскостью Q (Рис. 6.5.). Линии их пересечения позволяют выделить из всех плоскостей  две, которые ориентированы к падающему лучу под углом θ 1. Нормали их N1 и N2. Заметим также, что отраженный луч, нормаль N1 и So всегда лежат в одной плоскости.
две, которые ориентированы к падающему лучу под углом θ 1. Нормали их N1 и N2. Заметим также, что отраженный луч, нормаль N1 и So всегда лежат в одной плоскости.
Отраженный луч для плоскостей, соответствующих нормали N1, пойдет в плоскости, образованной падающим лучом и N1. Эта плоскость пересечет фотопленку по прямой AB, причем угол 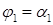 , как это следует из Рис. 6.5. Положение нормали N2 относительно вертикальной оси также определяется углом φ1, поэтому на электронограмме пятно дифракции должно расположиться симметрично первоначальному пятну относительно осей электронограммы.
, как это следует из Рис. 6.5. Положение нормали N2 относительно вертикальной оси также определяется углом φ1, поэтому на электронограмме пятно дифракции должно расположиться симметрично первоначальному пятну относительно осей электронограммы.
Рассуждая аналогичным образом, можно показать, что и для всех других плоскостей  , не перпендикулярных оси текстуры
, не перпендикулярных оси текстуры 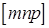 , дифракционный луч должен дать пятна на электронограмме, симметричные относительной вертикальной оси электронограммы.
, дифракционный луч должен дать пятна на электронограмме, симметричные относительной вертикальной оси электронограммы.
В том случае, если угол между нормалью к плоскости и осью текстуры φ =0º, т.е. плоскости перпендикулярны к оси текстуры, то и α =0º. Следовательно, пятно дифракции для таких плоскостей должно лежать на оси симметрии электронограммы (на оси х). Мы знаем, однако, что индексы плоскости (НКL) и нормали к ней  в кристаллах кубической сингонии всегда совпадают, поэтому индексы пятен, лежащих на оси x электронограммы, должны определять индексы оси текстуры
в кристаллах кубической сингонии всегда совпадают, поэтому индексы пятен, лежащих на оси x электронограммы, должны определять индексы оси текстуры 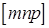 . Таким образом, индицируя электронограмму, мы определяем, какая из внутренних кристаллографических осей располагается в пленке перпендикулярно подложке.
. Таким образом, индицируя электронограмму, мы определяем, какая из внутренних кристаллографических осей располагается в пленке перпендикулярно подложке.
Следует помнить, однако, что между углами α и φ всегда существует небольшая разница в силу того, что в реальном случае не имеют мест допущения, принятые вначале: перпендикулярность  и оси текстуры
и оси текстуры 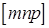 , вырождение дебаевского конуса в плоскость Q. Но эта разница между углами α и φ не превышает единицу или доли градуса и практически ею можно пренебречь.
, вырождение дебаевского конуса в плоскость Q. Но эта разница между углами α и φ не превышает единицу или доли градуса и практически ею можно пренебречь.
Расчет электронограммы текстурированного образца. Первоначально по электронограмме определяем набор d, согласно соотношению (6.7), которое мы рассмотрели ранее. Затем необходимо проиндицировать рефлексы-дуги. Для кубических кристаллов сумму квадратов индексов для каждого пятна можно получить из известного соотношения:  , если нам известно а из таблиц и рассчитанные значения d. Найдя сумму квадратов индексов, по таблицам (см. метод Дебая) определяют сами индексы плоскостей, соответствующие данному кольцу электронограммы. Симметричное расположение пятен на электронограмме относительно вертикальной оси x дает основание предполагать присутствие оси аксиальной текстуры, перпендикулярной подложке. (Это проверяется контрольным снимком образца, повернутого на 45–50º в плоскости подложки. В случае аксиальной текстуры вид электронограммы не должен измениться.)
, если нам известно а из таблиц и рассчитанные значения d. Найдя сумму квадратов индексов, по таблицам (см. метод Дебая) определяют сами индексы плоскостей, соответствующие данному кольцу электронограммы. Симметричное расположение пятен на электронограмме относительно вертикальной оси x дает основание предполагать присутствие оси аксиальной текстуры, перпендикулярной подложке. (Это проверяется контрольным снимком образца, повернутого на 45–50º в плоскости подложки. В случае аксиальной текстуры вид электронограммы не должен измениться.)
Для определения индексов оси аксиальной текстуры выбирают пятна, расположенные на оси симметрии электронограммы x. Если, к примеру, на оси электронограммы расположены пятна 001, 002 и т.д., то осью аксиальной текстуры в кубических кристаллах будет направление  . Определив индексы оси текстуры, правильность определения можно проверить, воспользовавшись уже известной формулой для углов в кубической решетке:
. Определив индексы оси текстуры, правильность определения можно проверить, воспользовавшись уже известной формулой для углов в кубической решетке:
 (6.8)
(6.8)
где m, n, p – индексы оси текстуры;
H, K, L – индексы отражающей кристаллографической плоскости.
Вычисляя по этой формуле всевозможные углы φ, учитывают не только численные значения индексов плоскостей, но и различные перестановки индексов, а также комбинации знаков. Так, например, при определении угла между осью текстуры [ mnp ] и нормалями к плоскостям (311) подставляют последовательно в формулу (6.8) индексы  и т.д., производя перестановки чисел и знаков. Это соответствует всем эквивалентным плоскостям, у которых, как известно, одно и то же межплосткостное расстояние и, следовательно, рефлексы-дуги должны располагаться на кольце одного радиуса.
и т.д., производя перестановки чисел и знаков. Это соответствует всем эквивалентным плоскостям, у которых, как известно, одно и то же межплосткостное расстояние и, следовательно, рефлексы-дуги должны располагаться на кольце одного радиуса.
При расчете по формуле (6.8) могут получиться различные значения угла φ. Расчетные углы φ и установленные экспериментально углы a, измеренные по положению различных интерференционных пятен на кольце одного радиуса (Рис. 6.5) должны совпадать.
ЗАДАНИЕ
1. Определить радиусы интерференционных колец, на которых располагаются отражения.
2. Измерить угловое расположение рефлексов на электронограмме.
3. Определить межплоскостное расстояние.
4. По индексам оси текстуры рассчитать углы φ для различных индексов отражающих плоскостей, сравнить с эксперементальными результатами.