Практическая работа №8 ОПРЕДЕЛЕНИЕ СОСТАВА квазибинарного ТВЕРДого РАСТВОРа по дифрактограмме

Цель работы – ознакомление с одним из методов фазового анализа и определения состава твердых растворов, подчиняю­щихся правилу Вегарда, в системах с неограниченной раствори­мостью.

Твердыми растворами называются кристаллические много­компонентные системы, в которых изменение соотношения меж­ду компонентами не нарушает их однофазность.

Твердые растворы разделяют на 3 типа: внедрения, замеще­ния (неупорядоченные и упорядоченные) и вычитания.

Твердые растворы внедрения образуются чаще всего при растворении элементов с малыми эффективными радиусами. В частности, если растворяемый компонент существует в виде иона с малым ионным радиусом, например, Li⁺, Cu⁺ в решетках герма­ния и кремния. Атомы растворенного компонента располагаются в межузлиях растворителя и образование твердых растворов вне­дрения всегда сопровождается увеличением объема элементарной ячейки. Кроме того, появление дополнительных частиц в межуз­лиях приводит к изменению симметрии решетки твердого раство­ра. Тип твердого раствора внедрения, как это следует из меха­низма его формирования, предполагает наличие только ограни­ченной растворимости.

Понятие твердых растворов вычитания введено первона­чально для химических соединений, переменный состав которых подчеркивается формулой, например TiO_x, где х является пере­менной величиной, меняющейся в значительных пределах (десятков % ат.). В твердых растворах вычитания некоторая часть узлов в решетке оказывается незанятой.

Полупроводниковые соединения, содержащие значитель­ное количество вакансий (10^-2 – 10^-3 % ат.), также рассматривают­ся как твердые растворы вычитания. Твердые растворы вычита­ния трактуются в рамках соотношения количества компонентов и отклонения от стехиометрии состава соединений. Системы на ос­нове твердых растворов вычитания, как и внедрения, характери­зуются ограниченной растворимостью.

Третьим типом твердых растворов являются твердые рас­творы замещения. При образовании неупорядоченного твердого раствора по типу замещения атомы растворяемого вещества за­нимают позиции атомов растворителя в решетке статистически равномерно, что сопровождается либо уменьшением размера элементарной ячейки твердого раствора, если размер растворяе­мого атома меньше, либо увеличением при обратном соотноше­нии. Если компоненты такого раствора кристаллохимически су­щественно различаются, то система будет иметь ограниченную взаимную растворимость в твердом состоянии. Однако при обра­зовании твердых растворов по типу замещения появляется редкая возможность получения непрерывного ряда твердых растворов, которые в дальнейшем мы будем называть твердыми растворами с неограниченной растворимостью (ТР_НР).

Требования, предъявляемые к компонентам при образова­нии ТР_НР, следующие.

Изоморфность кристаллической структуры компонентов предполагает сходство их химических свойств и размеров, что предопределяет возможность образования изоструктурных твер­дых растворов замещения.

Различие в размерах двух взаимодействующих атомов огра­ничивает взаимную растворимость, даже несмотря на изострук­турность компонентов раствора. Согласно правилу Юм-Розери отношение атомных размеров считается «благоприятным» для взаимной растворимости, если разность диаметров меньше 15%; для совершенно изоморфных систем эта величина ≤ 5-7%.

Впоследствии это было обосновано расчетами, основанными на анализе энергии упругих деформаций при внедрении в кристал­лическую решетку растворителя инородных атомов растворяемо­го вещества.

Компоненты, сильно отличающиеся по своим химическим свойствам (электроотрицательности, валентности и т.д.), склонны к образованию устойчивых химических соединений. Область пер­вичных твердых растворов в таких системах оказывается незна­чительной, а образование ТР_НР делается невозможным.

Для очень многих систем с неограниченной растворимо­стью установлена линейная зависимость величины параметров кристаллической решетки от содержания компонентов твердого раствора - так называемый закон Вегарда. На рис. 8.1 и 8.2 пред­ставлены изменения параметров элементарной ячейки твердых растворов в зависимости от состава ТР_НР. Кроме того, даны при­меры штрих-диаграмм, соответствующих изменениям составов и дифракционных картин чистого компонента А, твердого раствора A_1-х В_х и чистого компонента В. По характеру изменения дифракционной картины видно, что при изменении состава твер­дого раствора происходит простое смещение положения дифрак­ционных линий (изменение брэгговских углов). Рис. 8.1 относит­ся к системе с компонентами А и В, кристаллизующимися В кубической сингонии (параметр решетки а), а рис. 8.2 соответствует компонентам с элементарными ячейками гексагональной сингонии (параметры а и с). Для систем, изображенных на рис. 8. 1 и 8.2, формула твердого раствора запи­сана как A_1-х ·В_х. При такой записи х выражен в атомных долях (ат. д.). Если х = 0, то имеем чистый компонент А если х = 1 то чистый компонент В, 0≤ х ≤ 1. Для кубических кристаллов (рис. 8.1) имеют место соотношения

а = а_А + x (а_В – а_А) или x = (а – а_А) / (а_В – а_А) (8.1)

Аналогично, для системы, изображенной на рис. 8.2, линей­ность изменения параметров а и с твердого раствора приводит к соотношениям

а = а_А + x (а_В – а_А), c = c_А + x (c_В – c_А) (8.2)

или x = (а – а_А) / (а_В – а_А), x = (c – c_А) / (c_В – c_А) (8.3)

Параметры решетки твердого раствора определяются по дифрактограмме.

Лишним подтверждением сказанного о необходимости вы­полнения всех трех требований к компонентам для образования ТР_НР являются сочетания элементов одной IV группы периодиче­ской системы. В этом случае не всегда образуются твердые рас­творы: так Ge и α-Sn лишь незначительно растворяются друг в друге, Si и Ge дают непрерывный ряд ТР_НР, в случае же Si и С – образуется химическое соединение SiC. Причинами, препятствующими образованию ТР_НР, являются: значительное разли­чие атомных размеров, как это имеет место в системе Ge и α-Sn или превалирующая склонность к образованию химического со­единения в системе Si-C. Как уже упоминалось, Ge и Si, удовле­творяющие всем трем требованиям, в действительности образуют системы твердых растворов с одним и тем же типом элементар­ной ячейки (тип алмаза) и линейно меняющимся периодом а, аналогично представленным на рис. 8.1.

Рис. 8.1. Зависимость параметра решетки и вида штрих-диаграмм от состава

Рис. 8.2. Зависимость параметров решетки и вида штрих-диаграмм от состава

В случае систем с ограниченной растворимостью в твердом состоянии вся область изменения составов может быть разделена на три участка, для которых изменение параметров решетки мо­жет быть охарактеризовано схемами рис. 8. 3, а и 3, б. Предпола­гается, что системы, представленные на этих рисунках образова­ны неизоморфными компонентами кубической симметрии (рис. 8. 3, а) или компонентами кубической и гексагональной сим­метрии (рис. 8. 3,б). В обеих системах есть области (I и III), соот­ветствующие образованию однофазного твердого раствора на основе решетки растворителя с линейным изменением параметров решетки последнего.

А) б)

Рис. 8.3. Зависимость параметров решетки от состава в системе с элементарными компонентами кубической (а) или кубической и гексаго­нальной (б) симметрии

Нарушение одного из правил образования ТР_НР (изоморф­ность компонентов) приводит к ограниченной растворимости компонентов и, следовательно, к появлению области (II), где од­новременно существуют два типа твердых растворов с неизмен­ными параметрами элементарных ячеек. Изменение состава в этой двухфазной области приводит лишь к изменению количественных соотношений между двумя типами твердых растворов и изменению интенсивности дифракционных линий фаз с уже уста­новившимися постоянными параметрами.

Как правило, изменение параметров в I и III областях по­добных систем имеет линейный характер и, следовательно, если есть данные о пределах взаимной растворимости компонентов, то подобные линейные зависимости также можно использовать для определения составов твердых растворов в пределах соответст­вующих областей гомогенности.

Особый случай неизоморфных компонентов системы пред­ставляет пара кубическая гранецентрированная (ГЦК) и гексаго­нальная плотнейшие упаковки (ГПУ) сфалерит (s) и вюрцит (w). С термодинамической точки зрения две различные структурные модификации одного химического состава являются двумя раз­личными фазами. Пример такой системы представлен на рис. 8.4, где компоненты являются элементарными веществами (х выражен в % ат.).

Рис. 8.4. Зависимость параметров решетки от состава

Как известно, структуры ГЦК и ГПУ являются двумя вари­антами плотнейших упаковок: трехслойной и двухслойной. Рас­стояние между слоями в направлении [111] кубической и [0001] гексагональной решетки соответственно, обозначим h. Связанное с параметрами обоих решеток расстояние h с составом изменяет­ся (рис. 8. 4), как и параметры, но непрерывно во всем диапазоне составов. В связи с этим межплоскостное расстояние между слоями плотнейших упаковок может быть использовано для оп­ределения х

x = (h – h _А) / (h _В – h _А) (8.4)

Параметры решеток сосуществующих фаз в системе меняются линейно, но в ограниченных областях I – II для а^к и II – III для а^г, с^г (рис. 8.4). Для построения линейной зависимости Вегарда, в случае отсутствия второй модификации у компонентов, могут быть использованы соотношения теории плотнейших шаровых упаковок

h = 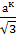= = откуда а^к = а^г ; а^к = с^г (8.5)

Особый интерес представляет воз­можность образования твердых растворов между компонентами, каждый из которых представляет из себя не элементарное вещество, а бинарное соединение – так называемые квазибинарные систе­мы. Так, эксперимен­тально доказано обра­зование ТР_НР в том случае, когда крайние члены изоструктурны (например, сфалерит s₁-s₂ или вюрцит w₁-w₂), независимо от того – имеет ли место анионный (В) или катионный (А) изоморфизм. Изменение параметров решетки в квазибинарной системе проявляется так же, как если бы компоненты твердого раствора были элементарными веществами (т.е. аналогично рис. 8.1 или 8.2).

В некоторых случаях неограниченная растворимость на­блюдается, если компоненты квазибинарного твердого раствора неизоструктурны, но имеют очень близкие по типу решетки (s-w). Для них будут верны соотношения, опреде­ляющие изменения параметров решетки от состава твердого рас­твора. Примером могут служить твердые растворы замещения на основе соединений ZnSe (s) и CdSe (w), представленные на Рис. 8.5.

Экспериментально было показано, что значения параметров решетки этих твердых растворов очень хорошо ложатся на прямые линии, что свидетельствует о выполнении закона Вегарда как во вюрцитной, так и в сфалеритной областях. При этом сплошные участки прямых на Рис. 8.5 совпадают с эксперимен­тальными данными, а пунктир соответствует экстраполяции до значений а^к ZnSe и а^г, с^г CdSe.

Поскольку крайние члены этой системы при­надлежат к различным, хотя и близким, струк­турным типам, то существует переходная об­ласть, в которой проис­ходит смена кристалличе­ской структуры.

Рис. 8.5. Зависимость параметров решетки от состава в системе Zn_l-xCd_xSe

Формулу твердого раствора в квазибинарной системе можно записать как (ZnSe)_1-х· (CdSe)_x или Zn_l-xCd_xSe, где х в отличие от простых бинарных систем соответствует мольным долям (м.д.), характеризующим вклад соединений как компо­нентов, хотя в кристалли­ческой решетке твердого раствора можно обнару­жить лишь атомы, но не молекулы растворенного вещества. При необходимости используют % ат.: м.д.· 100 = % мол. = 2· % ат.

В заключение следует отметить, что анализ составов ТР_НР на основании изменения параметров кристаллической решетки широко используется для контроля полупроводниковых моно- и поликристаллических слитков. Прецизионные методики съемки на дифрактометре дают информацию о межплоскостных расстояниях с точностью 10^-4 – 10^-5 Å. Это позволяет определить состав, например, для системы ZnSe·CdSe, с точностью 10^-2– 10^-3 % мол., что соизмеримо с колебаниями состава по слитку.

Для кристаллов кубической сингонии расчет параметра элементарной ячейки а можно провести, используя соотношения

или a = d (8.6)

а для гексагональной сингонии

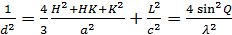(8.7)

где d - межплоскостное расстояние, λ - длина волны, Н, К, L ­индексы интерференции.

ЗАДАНИЕ

1. Состав твердого раствора изучается по дифрактограмме, снятой на дифрактометре ДРОН-4-07 при измельчении монокристаллических проб. Необходимо ознакомиться с дифрактограммой и разобраться с информацией, представленной в распечатке к ней.

2. Пользуясь справочными данными, найти характеристики структуры компонентов предлагаемого для изучения квазибинарного твер­дого раствора. Построить зависимость параметров а, с и h от х, % мол. на основании закона Вегарда.

3. Определить по дифрактограмме фазовый состав (одно-, двухфазная система) и тип структуры (s, w) предложенного твер­дого раствора.

4. После идентификации всех рефлексов дифрактограммы зарисовать ее в отчете в виде схемы - штрих-диаграммы.

5. Заполнить таблицу 8.1, воспользовавшись информацией, данной в распечатке на дифрактограмме и расчетными значениями параметров твердого раствора.

Таблица 8.1

Характеристика структуры состава_______________ при λ =__________Å

6. Определить состав твердого раствора по среднему значе­нию параметра(ов) а, с и h. Нанести значения х, % мол. на предварительно построенный гра­фик (п.2).