Цель работы – ознакомление с рентгеновским методом исследования монокристалла. Определение периода идентичности вдоль оси вращения кристалла и индицирование рентгенограммы вращения.
Расчет рентгенограмм вращения, снятых при соответствующей ориентировке кристалла, позволяет определить периоды идентичности вдоль осей, перпендикулярных рентгеновскому пучку, а, следовательно, получить сведения о параметрах и типе элементарной ячейки.
Съемка по методу вращения осуществляется на монохроматическом рентгеновском излучении. Для получения рентгенограммы вращающегося кристалла ортогональных систем образец устанавливается так, чтобы одна из его главных кристаллографических осей совпадала с осью вращения, а рентгеновский пучок был направлен нормально этой оси. Толщина исследуемого кристалла должна быть не слишком малой, т.к. при этом уменьшается количество отражающих плоскостей и резко возрастает экспозиция при съемке, но не слишком велика, поскольку рентгеновские лучи сильно поглощаются образцом. Обычно применяют при съемке рентгенограмм вращения, также как и при съемке лауэграмм, образцы толщиной 0,1 – 0,5 мм.
Типичная рентгенограмма вращения приведена нарис. 5.1.
Рис. 5.1. Схема рентгенограммы вращения.
При съемке монокристалла методом вращения отраженные лучи расходятся от него в виде дискретных лучей, лежащих на поверхности коаксиальных конусов, ось которых параллельна оси вращения образца. Поместим теперь вокруг оси вращающегося кристалла фотопленку, изогнутую по цилиндру (рис. 5.2). Дифракционные лучи пересекут цилиндрическую фотопленку по параллельным окружностям, которые на распрямленной пленке (рис. 5.2) имеют вид прямых линий. Эти линии называются слоевыми. Дискретные дифракционные лучи, попадая на фотопленку, вызывают на ней почернения в виде отдельных пятен. Каждая из слоевых линий является своеобразным отражением соответствующих узловых плоскостей обратной решетки. Так, плоскость обратной решетки, пересекающая ось x* в начале координат, дает среднюю так называемую нулевую слоевую линию на рентгенограмме (рис. 5.2). Плоскость, отсекающая на оси x* отрезок, равный единице, дает первую слоевую линию и т.д., то есть каждая слоевая линия отвечает определенному целому числу n, которое определяет число единичных отрезков, отсекаемых плоскостью обратной решетки на оси x*.
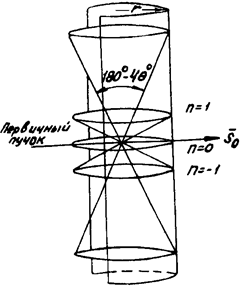
Рис. 5.2. Образование слоевых линий при съемке с вращением на цилиндрической пленке.
Нулевая слоевая линия принимается за начало отсчета других линий. Она проходит через первичное пятно (рис. 5.2) и делит рентгенограмму на две симметричные части: верхнюю и нижнюю. Слоевые линии располагаются симметрично по обе стороны от нулевой, причем первая симметричная линия вверх от нее называется плюс первая, а вниз – минус первая, вторая слоевая линия вверх – плюс вторая, а вниз – минус вторая и т.д.
Существует определенная взаимосвязь между обозначениями слоевых линий на рентгенограмме и индексами пятен, расположенных на ней.
Рассматривая пятна, расположенные на нулевой слоевой линии и, следовательно, узлы нулевого слоя обратной решетки, мы приходим к выводу, что все они соответствуют отражениям рентгеновских лучей от атомных плоскостей с индексами (0kl). Узлы первого слоя обратной решетки, дающие пятна первой слоевой линии, имеют индексы [[1kl]], что соответствует индексам отражающих плоскостей (1kl) и т.д.
Рассуждая подобным образом далее, приходим к выводу, что номер слоевой линии на рентгенограмме определяет первый индекс дифракционного пятна. Это значит, что в рассмотренном нами случае первый индекс всех пятен нулевой слоевой линии равен нулю, для первой слоевой линии индекс будет 1, для второй 2 и т.д.
При рассмотрении рентгенограмм вращения следует учитывать также и то, что благодаря правилам погасания на них могут присутствовать не все пятна. За счет погасания ряда отражений в сложных ячейках пятна, расположенные на некоторых слоевых линиях, могут пропадать; тогда очевидно, номер слоевой линии не соответствует номеру слоя обратной решетки.
Расстояние между слоевыми линиями Ln является функцией периода идентичности атомного ряда, расположенного вдоль оси вращения кристалла. Обозначим период идентичности атомной решетки по оси вращения через I и расстояние между плоскостями обратной решетки по этой оси через d*. Между этими величинами, как следует из построения обратной решетки, существует зависимость
I = 1/d* (5.1)
Таким образом, определив величину d*, можно вычислить период идентичности I по оси вращения кристалла.
Рис. 5.3. К определению периода идентичности по рентгенограмме вращения.
Изрис. 5.3 видно, что sinan = (nd*)l, откуда
d*= 
. (5.2)
Угол an определяется по расположению слоевых линий на рентгенограмме вращения (рис. 5.3)
tgan=Ln/r. (5.3)
Здесь n – номер слоевой линии, Ln – расстояние от нулевой слоевой линии до n-ой, r – радиус камеры вращения, в которой помещается фотопленка.
На практике рекомендуется измерять расстояние 2Ln, то есть расстояние между положительной (n) и отрицательной (–n) симметричными слоевыми линиями. Тогда результаты определения периода идентичности получаются более точные. При этом получим:
(5.4)
где D – диаметр камеры вращения.
Из последней формулы находим угол an, значение которого подставляем в формулу для d*. В результате получим, что период идентичности вдоль оси вращения кристалла
I = 1 / d* = nl / sin (arctg (2Ln / D)). (5.5)
В общем случае размеры элементарной ячейки при съемке методом вращения определяются по трем рентгенограммам, снятым при вращении вокруг 3-х основных внутренних кристаллографических осей.
Тип ячейки Бравэ выявляется при сравнении периодов идентичности вдоль осей [100], [110], [111]. Окончательное заключение о типе ячейки Бравэ делается после индицирования рентгенограммы. Этот вывод следует согласовать с числом частиц в элементарной ячейке, расчет которого приводился при рассмотрении метода порошков.
Задача индицирования рентгенограмм вращения, снятых по одному из векторов a, b или c, состоит в определении только двух индексов интерференционных пятен. Мы уже говорили, что третий индекс интерференционного пятна равен номеру слоевой линии, на которой он находится. Допустим, что снимался кристалл кубической сингонии. Вращение осуществлялось вокруг оси a*. Тогда первый индекс всех интерференционных пятен известен: для нулевой слоевой линии он равен 0, для 1-ой слоевой линии первый индекс равен 1 и т.д. Таким образом, индицирование сводится к определению только индексов K и L.
Индексы интерференции каждого рефлекса нарентгенограмме вращения можно определить, зная величину вектора Hhkl обратной решетки и угол скольжения q.
Величина вектора H для любого интерференционного пятна определяется из соотношения ½ H ½=1/d. Подставляя в эту формулу значение d из уравнения Вульфа-Брегга (2dsinq=l), получим
½ H ½=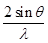 
(5.6)
Для кубической сингонии (a=b=c): 
= ê H ê2, откуда
H2+K2+L2 = (êHê/a*)2 = (êHê× a)2 (5.7)
Для разных слоев рентгенограммы вращения:
0-слой (0, K, L) (êHê× a)2 = K2+L2
1-ый слой (1, K, L) (êHê× a)2 = K2+L2+1 или K2 + L2 = (êHê×a)2 – 1
2-ой слой (2, K, L) (êHê× a)2 = K2+L2+4 или K2 + L2 = (êH ê×a)2 – 4
3- ий слой (3, K, L) (êHê× a)2 = K2+L2+9 или K2 + L2 = (êHê×a)2 – 9 (5.8)
Соотношение (5.8) позволяет вычислить сумму квадратов интересующих нас индексов K и L, а воспользовавшись табл. 5.1, и эти индексы, что приемлемо для всех слоевых линий, если определен угол скольжения q.
Для нулевой слоевой линии расчет у гла скольжения q рентгенограммы следующий: промеряем расстояние 2l между двумя симметричными пятнами нулевой слоевой линии и определяем угол отражения q по формуле (аналогично расчету дебаеграммы):
2q 0 = 
(5.9)
где r – радиус цилиндрической камеры вращения. Далее отделяем пятна b-излучения (при съемке без фильтра), учитывая признаки b-отражений и используя соотношение
sin qa / sin qb = la / lb (5.10)
Для каждого пятна a-излучения вычисляем угол q°, абсолютную величину вектора H (5.6) и, воспользовавшись соотношением (5.8), определяем (êH ê× a)2 как и недостающие индексы К, L по табл. 5.1. Данные расчета заносим в таблицу.
Для пятен на n-слоевой линии вектор H не лежит в плоскости n-слоя обратной решетки (рис. 5.3). Поэтому определяем угол отражения q для пятен n-ой слоевой линии из прямоугольного сферического треугольника А Pn¢ P0 (рис. 5.4), который является частью сферы с радиусом r.
Рис. 5.4. Определение угла скольжения q по положению пятен в n-слое
cos 2q = cos 2b × cos an (5.11)
Угол an получаем из формулы (5.3). Для определения угла b имеем, как и в случае 0-слоя,
b=57,3 
(5.12)
где l – расстояние от средней линии симметрии рентгенограммы вращения P0P0¢ (рис. 5.4) до интерференционного пятна Pn. Так как удобнее измерять расстояние между двумя симметричными пятнами на одной слоевой линии, то есть 2 l, причем в данном случае ошибка сильно уменьшается, то формула для определения угла b
2b=57,3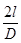 
(5.13)
Пятна от Kb-излучения для n-ой слоевой линии (n¹0) выявляются сразу, так как они лежат несколько ниже пятен Ka-излучения вдоль прямых, идущих от a-пятен к выходу первичного пучка (пятно в центре рентгенограммы).
Определив угол отражения q0 из (5.11), далее вычисляем для каждого пятна вектор H, (ê H ê× a)2 и по табл. 1 индексы К и L. Данные расчета заносим в таблицу.
Таблица 5.1.
Значения (K2 + L2) при заданных K и L.
| L K | ||||||
ЗАДАНИЕ
1. Определить по рентгенограмме вращения период идентичности вдоль оси вращения кристалла.
2. Определить индексы интерференционных пятен нулевой слоевой линии, зная, что для съемки использовались кристаллы с кубической решеткой, а ось вращения устанавливалась параллельно оси a*.
3. Индицировать пятна ненулевых слоевых линий. Результаты занести в таблицу.