Цель работы – ознакомление с понятиями базиса ячейки, атомного фактора, структурной амплитуды, формулировка правил погасаний.
Примитивная ячейка может быть охарактеризована одним атомом. За координаты его выбираются [[000]]. Поскольку, в простой пространственной решетке каждый узел одновременно принадлежит восьми соседним элементарным ячейкам и таких узлов в вершинах примитивной элементарной ячейки восемь, то на долю одной ячейки приходится 1 узел. Таким образом, узел [[000]] определяет число (и координаты) атомов, приходящихся на одну примитивную ячейку. Это базис данной ячейки. Запишем базис примитивной ячейки как (000).

Рис. 2.1. Базис объемно- (а) и гранецентрированной (б) ячеек.
Объемноцентрированная элементарная ячейка, которую можно представить составленной из двух примитивных (рис. 2.1,а), имеет 2 базисных атома. Один из них определяет не сдвинутую ячейку и имеет координаты [[000]], второй характеризует ячейку, смещенную на половину диагонали куба, и имеет координаты [[ 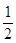
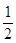
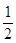 ]]. Таким образом, базис объемноцентрированной ячейки (000,
]]. Таким образом, базис объемноцентрированной ячейки (000, 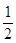
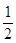
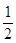 ).
).
Гранецентрированная ячейка, которую можно разложить на 4 примитивных (рис. 2.1,б), имеет 4 базисных атома. За базисный атом в каждой из трех сдвинутых примитивных ячеек выбираются ближайший к началу координат. Тогда базис гранецентрированной ячейки запишется как (000, 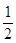 0
0 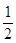 , 0
, 0 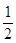
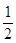 ,
, 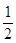
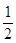 0).
0).
При рассмотрении пространственной решетки также можно прийти к выводу, что на одну гранецентрированную элементарную ячейку приходится 4 атома, а на одну объемноцентрированную 2, если учесть что к одной элементарной ячейке относится 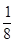
 атома в вершине,
атома в вершине, 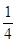 атома на ребре,
атома на ребре, 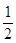 атома на грани и 1 в центре объема элементарной ячейки. Таким образом, число атомов в базисе всегда равно числу атомов, приходящихся на одну элементарную ячейку. Поэтому при рассмотрении дифракции рентгеновских лучей при их прохождении через кристалл, можно говорить о рассеянии рентгеновских лучей группой атомовбазиса.
атома на грани и 1 в центре объема элементарной ячейки. Таким образом, число атомов в базисе всегда равно числу атомов, приходящихся на одну элементарную ячейку. Поэтому при рассмотрении дифракции рентгеновских лучей при их прохождении через кристалл, можно говорить о рассеянии рентгеновских лучей группой атомовбазиса.
Согласно кинематической теории интенсивность рассеяния одним атомом характеризуют его атомным фактором. Атомным фактором f называется отношение амплитуды волны, рассеянной атомом, к амплитуде волны, рассеянной электроном
f = Eат/Eэл . (2.1)
Поскольку интенсивность рассеянных лучей пропорциональна квадрату амплитуды (I~E2), то атомный фактор определяет интенсивность рассеяния атомом.

Рис. 2.2. К выводу формулы для структурной амплитуды.
Интенсивность лучей, рассеянных одним электроном в том или ином направлении, различна. Такое направленное рассеяние, или поляризация рассеянной волны, связана с направлением вынужденных колебаний электрона и определяется формулой Томпсона:
 ×
×  ×
×  , (2.2)
, (2.2)
где R – расстояние от рассеивающего электрона; 2q – угол между направлением падающего пучка и пучка рассеяния; I и I0 – интенсивность падающего и рассеянного пучков.
В атоме электроны не сосредоточены в одной точке, а распределены вокруг ядра в оболочке, размеры которой сравнимы с длиной волны. При расчете рассеивающей способности атома необходимо учесть интерференцию всех волн, рассеянных отдельными электронами. Если атом содержит Z электронов, мгновенное расположение которых в пространстве описывается радиусом-вектором ri, то мгновенное значение амплитуды, рассеянной атомом, будет равно:
Eат =  , (2.3)
, (2.3)
где sri – учитывает разность фаз, возникающую между волнами, рассеянными
i-электроном и электроном в начале координат.
Зная распределение (плотность) электронного облака свободного атома, амплитуду рассеяния Eат можно рассчитать теоретически. Она зависит от угла рассеяния и длины волны падающего излучения. В связи с этим величина атомного фактора f также будет зависеть от этих величин. Из опытных данных величину f можно получить, измеряя усредненные, например, по какому-то элементу объема, амплитуды рассеяния. Значения fтеор и fэксп достаточно хорошо совпадают. Для различных атомов они сведены в таблицы, дающие значения атомных факторов как функцию sinq/l.
В том случае, когда рассеяние рентгеновских лучей происходит в некотором объеме, то суммарная амплитуда луча дифракции будет зависеть от числа рассеивающих атомов, приходящихся на этот объем и их взаимного расположения, т.е. от числа атомов базиса и их координат.
Допустим, что в элементарной ячейке содержится 2 атома (рис. 2.2). Начало координат поместим в один из них, другой имеет координаты x, y, z. Если S0 и S единичные вектора на направлении падающего луча и луча рассеянного, то разность хода равна:
(R [ S – S0 ]) = d (2.4)
или разность фаз составит:
 d = j (2.5)
d = j (2.5)
Подставив значение d из (2.4) и (S – S0) из общего интерференционного уравнения получим:
j = 2p (HR) = 2p (Hx +Ky+Lz) (2.6)
Амплитуда рассеянной волны с такой разностью фаз запишется как:
F = fo eij (2.7)
Если в элементарной ячейке не 2 атома, а j базисных атомов, то
F =  eij (2.8)
eij (2.8)
Здесь f0 примерно соответствует амплитуде рассеяния одним атомом базиса, или атомному фактору, поэтому для разных базисных атомов суммарная амплитуда рассеяния одной элементарной ячейкой равна
F=  j e2pi (Hx+Ky+Lz) , (2.9)
j e2pi (Hx+Ky+Lz) , (2.9)
где x, y, z – координаты атомов базиса; fj – атомные факторы базисных атомов; H, K, L – индексы интерференции, определяющие, в частности, направление, в котором рассматривается рассеяние; j – число базисных атомов.
Величина F получила название структурной амплитуды. Структурная амплитуда показывает во сколько раз суммарная амплитуда лучей, рассеянных группой атомов базиса, больше амплитуды рассеяния одним электроном. Каждому отражению H, K, L соответствует своя структурная амплитуда. Величина, равная квадрату структурной амплитуды, называется структурным множителем.
Выражение для структурной амплитуды может быть записано и в другой форме. По формуле Эйлера eix = cos x + i sin x, поэтому можно записать:
F =  j cosjj + i
j cosjj + i  j sinjj , (2.10)
j sinjj , (2.10)
где jj = 2p (Hxj + Kyj +Lzj).
Подставив в выражение для структурной амплитуды координаты базиса различных типов элементарных ячеек кубической системы, определим, какие плоскости будут давать отражения. Суммируя результаты расчета структурных амплитуд, получим правила погасаний, характеризующие отсутствие отдельных отражений в решетке данного типа.
Когда элементарная ячейка включает атомы разных элементов, отражения будут давать все плоскости. Однако, когда рассеивающие способности атомов A и B близки между собой (fA»fB), то дифракционная картина будет примерно такой же, как и для идентичных атомов. Если же fA много больше или много меньше fB , то интерференционная картина сильно отличается от той, которую дают идентичные атомы.
ЗАДАНИЕ
1. Записать базис объемноцентрированной ячейки. Подставив координаты базиса в выражение для FHKL, произвести расчет структурной амплитуды для объемноцентрированной ячейки в случае, когда все атомы вещества идентичны. Определить, интерференционные линии каких плоскостей будут отсутствовать на рентгенограмме.
2. Сформулировать правило погасаний для объемноцентрированной ячейки.
3. Записать базис гранецентрированной ячейки. Вычислить структурную амплитуду гранецентрированной ячейки, считая, что элементарная ячейка состоит из идентичных атомов.
4. Сформулировать правило погасаний для гранецентрированной ячейки.