1). Анализируя (3.1) и учитывая (2.8) - (2.18) заключаем:
Циркуляция вектора 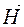 по контуру
по контуру  пропорциональна скорости изменения потока вектора
пропорциональна скорости изменения потока вектора  через поверхность
через поверхность 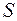 , ограниченную контуром
, ограниченную контуром  .
.
Физический смысл уравнения(3.1):
Переменное электрические поле возбуждает в пространстве вокруг вектора  ПЕРЕМЕННОЕ магнитное поле
ПЕРЕМЕННОЕ магнитное поле 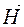 ВИХРЕВОГО ТИПА (рис. 3.1).
ВИХРЕВОГО ТИПА (рис. 3.1).
Вектор 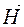 "циркулирует" в плоскостях ортогональных вектору
"циркулирует" в плоскостях ортогональных вектору  . Взаимное расположение векторов
. Взаимное расположение векторов 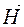 и
и  подчиняется правовинтовой системе.
подчиняется правовинтовой системе.
 Рисунок 3.1
Рисунок 3.1
Заметим, что символ «~» у векторов  ,
,  ,
,  ,
,  в уравнениях (3.1) - (3.4) опущен для простоты записи. На рис. 3.1 показана лишь одна условная силовая линия вектора
в уравнениях (3.1) - (3.4) опущен для простоты записи. На рис. 3.1 показана лишь одна условная силовая линия вектора  . Таких концентрических линий множество (рисунок 3.2). Следует, также, понимать, что сами силовые линии (любого поля) не более чем ГЕОМЕТРИЧЕСКИЕ образы, служащие лишь для иллюстрации соответствующих физических величин
. Таких концентрических линий множество (рисунок 3.2). Следует, также, понимать, что сами силовые линии (любого поля) не более чем ГЕОМЕТРИЧЕСКИЕ образы, служащие лишь для иллюстрации соответствующих физических величин  или
или  ,
,  или
или  .
.
Плоскость, в которой располагаются векторы 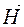 на рисунке 3.2 не является единственной. Таких "плоскостей" - множество (рис. 3.3).
на рисунке 3.2 не является единственной. Таких "плоскостей" - множество (рис. 3.3).

Рисунок 3.2

Рисунок 3.3
Таким образом, вихревое переменное магнитное поле  возникающее вокруг поля
возникающее вокруг поля  занимает некоторый объём ПРОСТРАНСТВА. Согласно уравнения (3.1) векторы
занимает некоторый объём ПРОСТРАНСТВА. Согласно уравнения (3.1) векторы  и
и  в однородном изотропном диэлектрике изменяются в ОДНОЙ ФАЗЕ, одновременно достигая максимума и минимума.
в однородном изотропном диэлектрике изменяются в ОДНОЙ ФАЗЕ, одновременно достигая максимума и минимума.
2). Анализируя (3.2) и учитывая (2.8) и (2.18) заключаем, что
Циркуляция вектора  по контуру
по контуру  пропорциональна взятой со знаком «-» скорости изменения потока вектора
пропорциональна взятой со знаком «-» скорости изменения потока вектора  через поверхность
через поверхность  , ограниченную контуром
, ограниченную контуром  .
.
Физический смысл уравнения (3.2):
Переменное магнитное поле возбуждает в пространстве вокруг вектора  ПЕРЕМЕННОЕ электрическое поле
ПЕРЕМЕННОЕ электрическое поле  ВИХРЕВОГО ТИПА (рис. 3.4). Вектор
ВИХРЕВОГО ТИПА (рис. 3.4). Вектор  циркулирует в плоскостях ортогональных вектору
циркулирует в плоскостях ортогональных вектору  . Взаимное расположение векторов
. Взаимное расположение векторов  и
и  подчиняется ЛЕВОвинтовой системе (на это указывает знак «-» в правой части уравнения (3.2)).
подчиняется ЛЕВОвинтовой системе (на это указывает знак «-» в правой части уравнения (3.2)).

Рисунок 3.4
Подобно рассмотренному вихревому полю  , вихревое поле
, вихревое поле  занимает некоторый объем пространства вокруг вектора
занимает некоторый объем пространства вокруг вектора  . В однородном изотропном диэлектрике векторы
. В однородном изотропном диэлектрике векторы  и
и  изменяются в одной фазе.
изменяются в одной фазе.
3). Рассмотренные два процесса, которые описываются уравнениями (3.1) и (3.2) неразделимы один от другого и представляют собой не что иное, как механизм возникновения и распространения в пространстве ЭЛЕКТРОМАГНИТНОГО ПОЛЯ или электромагнитной волны или, что то же самое - процесс распространения электромагнитных колебаний в пространстве. Пусть, например, в некоторой точке пространства возникло переменное поле  (рис. 3.1). Одновременно с ним возникает вихревое поле
(рис. 3.1). Одновременно с ним возникает вихревое поле  , которое к тому же является ПЕРЕМЕННЫМ. Переменному полю
, которое к тому же является ПЕРЕМЕННЫМ. Переменному полю  соответствует, согласно (3.6) переменная магнитная индукция
соответствует, согласно (3.6) переменная магнитная индукция  , которая согласно уравнения (3,2) (рис. 3.4) порождает вихревое поле
, которая согласно уравнения (3,2) (рис. 3.4) порождает вихревое поле  , которое опять же переменное, и ему соответствует переменная электрическая индукция
, которое опять же переменное, и ему соответствует переменная электрическая индукция  , согласно формулы (3.5). Далее процесс бесконечно повторяется. Так рождается и распространяется в пространстве электромагнитное поле (электромагнитная волна). Некоторое представление об этом процессе может дать рисунок 3.5:
, согласно формулы (3.5). Далее процесс бесконечно повторяется. Так рождается и распространяется в пространстве электромагнитное поле (электромагнитная волна). Некоторое представление об этом процессе может дать рисунок 3.5:
Рисунок 3.5
Для правильного понимания рисунка 3.5 еще раз напомним, что цепочка взаимосвязей

подчиняется правовинтовой системе.
Цепочка взаимосвязей:

подчиняется левовинтовой системе.
Более подробный анализ уравнений (3.1) и (3.2) показывает, что
во всякой электромагнитной волне векторы  ,
, 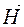 и
и  образуют правовинтовую систему координат, где
образуют правовинтовую систему координат, где  - вектор фазовой скорости распространяющейся электромагнитной волны (рис. 3.6) [8, стр. 199-207].
- вектор фазовой скорости распространяющейся электромагнитной волны (рис. 3.6) [8, стр. 199-207].

Рисунок 3.6
Из проведенного рассмотрения, очевидно, что при исходном векторе  , пульсирующем вдоль оси (
, пульсирующем вдоль оси ( ) декартовой системы координат (
) декартовой системы координат ( ) (рис. 3.5) электромагнитная волна распространяется не только вдоль оси (
) (рис. 3.5) электромагнитная волна распространяется не только вдоль оси ( ), как показано на рисунке, но и по любому другому направлению, параллельному плоскости (
), как показано на рисунке, но и по любому другому направлению, параллельному плоскости ( ).
).
4). Уравнение (3.З) свидетельствует лишь о том факте, что в однородном изотропном диэлектрике отсутствуют нескомпенсированные электрические заряды. Т.е. алгебраическая сумма положительных и отрицательных зарядов внутри диэлектрика равна 0. Поэтому в соответствии с теоремой Гаусса для вектора  ,
,  [8, стр. 304-312].
[8, стр. 304-312].
5). Из уравнения (3.4) следует, что поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
ВЕКТОР ПОЙНТИНГА
Введем вектор, определяемый как
 , (3.7)
, (3.7)
называемый в теории поля вектором ПОЙНТИНГА. Из правила векторного произведения и рисунка 3.6 следует, что вектор  совпадает по направлению с вектором фазовой скорости
совпадает по направлению с вектором фазовой скорости  (в однородном изотропном диэлектрике) и его модуль
(в однородном изотропном диэлектрике) и его модуль
 , (3.8)
, (3.8)
численно равен площади прямоугольника, построенного на векторах  и
и 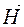 .
.
Теория электричества [8, стр. 96] и магнетизма [8, стр. 196], дает следующие значения плотности энергии электрической ( ) и магнитной (
) и магнитной ( ) компонент поля:
) компонент поля:
 , (3.9)
, (3.9)
 . (3.10)
. (3.10)
Найдем взаимосвязь плотности энергии электромагнитного поля
 (3.11)
(3.11)
с модулем вектора ПОЙНТИНГА ( ).
).
Из формул (3.9) и (3.10) следует, что
 (3.12)
(3.12)
 . (3.13)
. (3.13)
Поскольку в электромагнитной волне [8, стр. 308]
 , (3.14)
, (3.14)
из равенства (3.11) и (3.14) следует, что
 ,
,
 .
.
Заменяя  и
и  в (3.12) и (3.13) на
в (3.12) и (3.13) на  , получаем:
, получаем:
 (3.15)
(3.15)
 . (3.16)
. (3.16)
Подставляем (3.15) и (3.16) в (3.8):
 . (3.17)
. (3.17)
Подстановка в  числовых значений
числовых значений  и
и 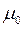 , указанных в (3.1) дает следующее значение:
, указанных в (3.1) дает следующее значение:
 ,
,
которое равно скорости электромагнитной волны в вакууме  .
.
Для практических расчетов значение  обычно принимают равным
обычно принимают равным
 .
.
Таким образом,
 , (3.18)
, (3.18)
Известно [8, стр. 286], что
 , (3.19)
, (3.19)
где  - фазовая скорость электромагнитной волны в однородном, изотропном диэлектрике с относительными проницаемостями
- фазовая скорость электромагнитной волны в однородном, изотропном диэлектрике с относительными проницаемостями  и
и  .
.
Поставляя (3.19) в (3.18) получаем:
 . (3.20)
. (3.20)