При анализе временной когерентности мы полагали, что волновые векторы в интерферирующих волнах имеют одно и тоже направление (рис. 7.2). Рассмотрим, к чему приводит нарушение этого условия
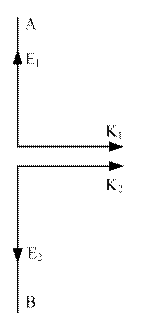
Рисунок 7.2 Рисунок 7.3
Пусть вектор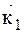 
составляет малый угол 
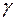с вектором 
. Как видно из рисунка 7.3, такой же угол образуется между линиями, вдоль которых располагаются векторы 
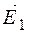и 
.
Заметим, что даже у самых совершенных лазеров в произвольном сечении лазерного пучка диаметром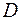 
(рис. 7.4), фаза волны, при переходе от одной точки волновой поверхности сечения к другой, изменяется случайным образом. Выберем в указанном сечении достаточно малую площадь диаметра 
с тем, чтобы в любой точке этого сечения фаза волны различалась не более чем на 
радиан. Будем считать, что монохроматичность излучения достаточно высока (
).
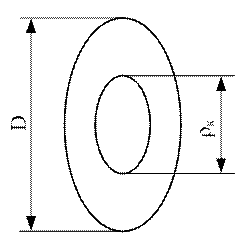
Рисунок 7.4 Рисунок 7.5
Пусть из центра (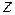
) волновой поверхности диаметра 
излучаются две волны и дают на экране (
) интерференционный максимум в точке (
) (рис. 7.6). Обе волны имеют волновой вектор величины 
.
Если в направлении точки () излучаются 2 волны из точки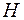 
, находящийся в нижней части круга, их интенсивность, при интерференции, распределится между максимумом в точке () и интерференционной линией в точке (
), лежащей выше точки (). Такое распределение обусловлено появлением компоненты скорости волны 
, связанной с изменением направления волнового вектора 
на угол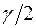 
.
Координату точки () можно найти из следующих соображений (рис. 7.6):
, 
,
, 
, 
,
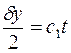где 
, 
.
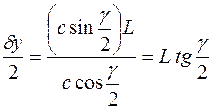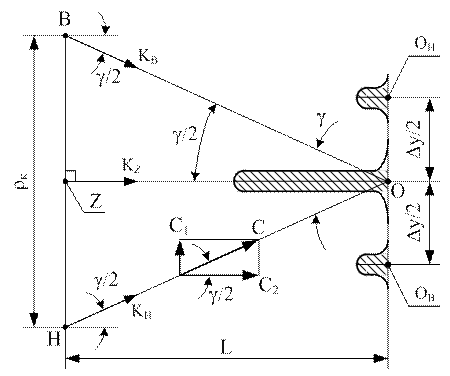
Рисунок 7.6
При малых ,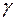 
.
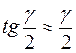Таким образом,
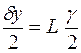, (7.10)
где 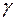- угол, выраженный в радианах.
Очевидно, что две волны с волновыми векторами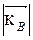 
, излучаемые из верхней части круга дадут добавочный максимум в точке (
) (рис.7.6), симметричной с (). Между, максимумами с координатами () и () будет располагаться множество максимумов, для которых вектор наклонен к (
) на угол 
.
Очевидно, любой максимум в интерференционной картине имеет сложную структуру с общей шириной 
(рис. 7.6, 7.7).
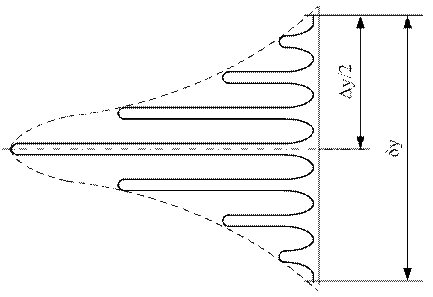
Рисунок 7.7
Рисунок 7.8
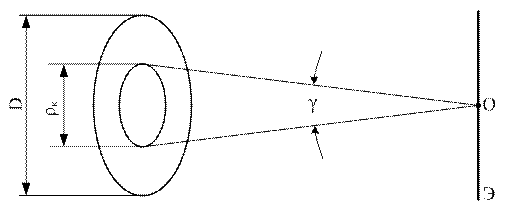
Рисунок 7.9
Измерительный прибор с малой разрешающей способностью (и тем более глаз наблюдателя) воспринимает этот набор максимумов как единую линию некоторого порядка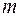 
. (в нашем случае 
) - пунктирная линия на рис.7.7.
Ширина линии, как следует из (7.10),
. (7.11)
Далее будет показано, что 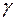и 
взаимосвязаны. По причинам историчесного характера величину обычно называют "радиусом" когерентности.
Очевидно, что ширина интерференционного максимума не может превышать расстояния между соседними максимумами (Δ 
):
, (7.12)
так как в противном случае интерференционная картина оказывается "смазанной". Условие (7.12) является одним из основных для получения интерференционного спектра. Найдем величину Δ с помощью рисунка 7.8, где 
подобен 
; 
; 
; 
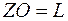- оптическая разность хода между волнами 1 и 2, интерферирующими в точке 
экрана (). Из подобия треугольников:
, 
(7.13)
где 
- координата максимума порядка 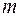, а
. (7.14)
Из (7.13) и (7.14)
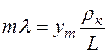. (7.15)
Для максимума порядка 
. (7.16)
Вычитая (7.15) из (7.16), имеем:
. (7.17)
Подставляя (7.17) и (7.11) в (7.12), получаем
, 
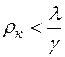. (7.18)
Соотношение (7.18) устанавливает взаимосвязь между длиной световой волны 
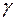, угловым размером (под которыми наблюдается из точки () экрана размер волновой излучающей поверхности, в пределах которого изменение фазы волны но превышает () радиан (рис. 7.9)) и, собственно радиусом когерентности 
.
ОБЪЕМ КОГЕРЕНТНОСТИ
Произведение площади круга диаметра на длину когерентности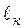 
называют объемом когерентности:
. (7.19)
ЗАКЛЮЧЕНИЕ
В заключение подчеркнем еще раз, что временная когерентность и её характеристики 
и 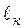определяются разбросом модуля волнового вектора 
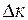, при его неизменном направлении.
Пространственная когерентность и, в частности , зависят прежде всего от различия в направлениях волновых векторов 
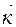, при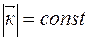 
.
На величину объема когерентности влияют как модули, так и направления волновых векторов.
Соблюдение условий (7.8) и (7.18) является необходимым для обеспечения выполнения закономерностей (5.30), (5.31), (5.33), (5.34), использующихся при анализе интерференционных задач.
КОНТРОЛЬНЫЕ ВОПРОСЫк главе 7
1. Понятие о длине, времени, радиусе, объеме когерентности. Какие параметры волнового вектора отражают эти понятия.
2. Сделайте вывод формул (7.9), (7.11), (7.17).
3. От чего зависит максимальный порядок, интерференционного максимума?
4. Как связано время когерентности с шириной полосы оптического излучения?