АНАЛИЗ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

 

Разделим (9.3) на :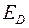

 

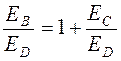. (9.9)

 

Известно [8, с. 70-72], что

 

, (9.10)

 

есть относительная диэлектрическая проницаемость вещества, кото­рая в нашем случае является частотно-зависимой физической вели­чиной. Из (9.1), (9.9), (9.10) следует, что

 

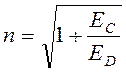. (9.11)

 

Представим результат разделения связанных зарядов 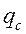(рис. 9.3, 9.5, 9.6) под влиянием внешнего поля в виде рис. 9.7. Полагая поле однородным, образованным двумя параллельными, бесконечными плос­костями, находящимися в идеальном вакууме (в междоузлиях кристал­лической структуры) (рис. 9.8), получаем, согласно теореме Гаусса [8, с. 57], напряженность поля связанных зарядов в виде:

 

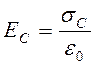, (9.12)

 

где

, (9.13)

 

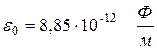- электрическая постоянная

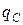- величина суммарного связанного заряда на торцевой поверхности диэлектрика (рис. 9.7), площадью .

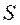Представим (9.13) в виде

 

, (9.14)

 

где 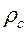- объёмная плотность связанных зарядов диэлектрика, заключенных в объеме .

 

 

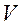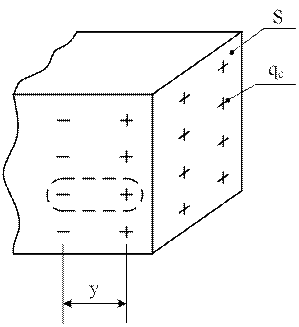
Рисунок 9.7

 

 

Рисунок 9.8

 

Подстановка (9.14) в (9.12) и (9.12) в (9.11) дает

 

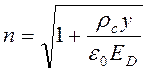. (9.15)

 

Вводя в (9.15) значение (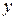) из решения (9.7) получаем:

 

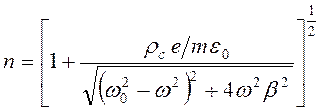. (9.16)

 

Формула (9.16) представляет собой результат решения задачи о на­хождении зависимости 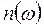для диэлектриков с единственным валентным электроном в узле структуры.

В общем случае, валентных электронов в окрестности любого иона более 1 (2, 3 и т.д.). В этом случае зависимость (9.16) услож­няется (см. далее.).

 

 

9.4. АНАЛИЗ ЗАВИСИМОСТИ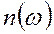

Пусть валентный электрон диэлектрика обладает малым коэф­фициентом затухания 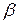, таким, что

 

. (9.17)

 

Обозначив 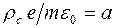и учитывая (9.17), получаем из (9.16):

 

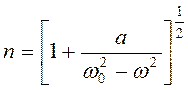, (9.18)

 

 

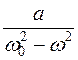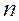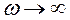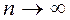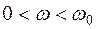Пусть и возрастает, - убывает, - возрастает, - возрастает. При , . Зависимость , для интервала показана на рисунке 9.9. При 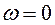(воздействие внешнего электромаг­нитного поля на валентный электрон отсутствует),

 

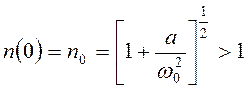. (9.19)

 

 

 

Рисунок 9.9

 

 

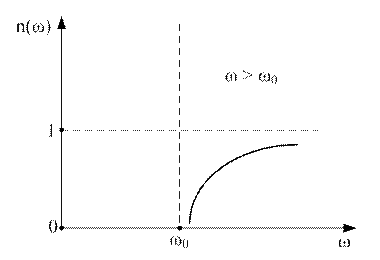
Рисунок 9.10

 

 

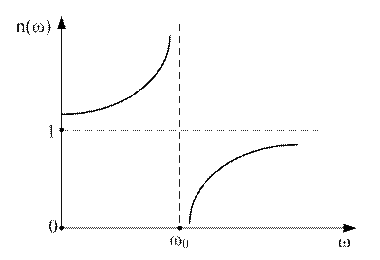
Рисунок 9.11

Пусть и по-прежнему возрастает. В этом случае, дробь 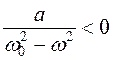, при любых . При достаточ­но больших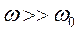

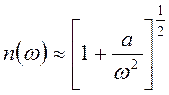, (9.20)

 

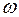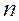и с ростом , - убывает, - возрастает.

В предельном случае (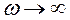), 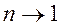(рис. 9.10). При 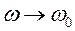, , 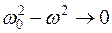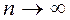· Объединяя два проведенных анализа, видим, что при 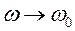, терпит разрыв, скачкообразно устремляясь в 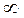(рис. 9.11). Такому поведению соответствует резонансное поглощение энергии волны валентным электроном, в результате чего амплитуда смещения его центра масс 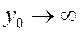(рис. 9.12).

Во всяком реальном диэлектрике валентный электрон обладает конечным коэффициентом затухания и его резонансная частота [4]

 

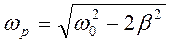. (9.21)

 

Амплитуда смещения также конечна:

 

. (9.22)

 

В результате зависимость приобретает вид, показанный на рисунке 9.14.

Резонансному поглощению энергии электромагнитной волны на частоте (рис. 9.13) соответствует резкое увеличение затухания сигнала в процессе его распространения по ВОЛС. Частота несущего оптического сигнала равная 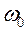неприменима для передачи его по ВОЛС, как неприменимы и частоты, лежащие в окрестности .

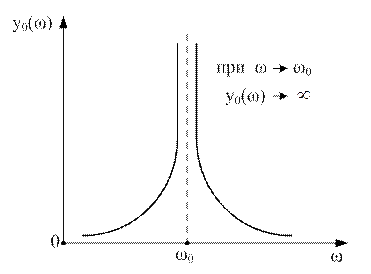
Рисунок 9.12

Рисунок 9.13

 

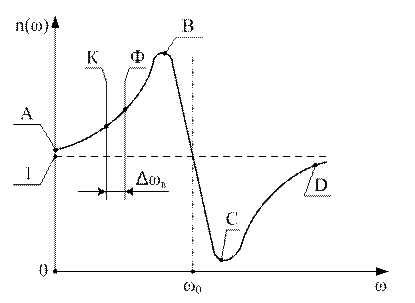
Рисунок 9.14

 

 

Рисунок 9.15

Рисунок 9.16

 

 

 

Рисунок 9.17

 

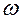Участки и (рис. 9.14) традиционно носят название областей "нормальной" дисперсии. На этих участках возрастает с ростом . Область 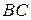, соответствующая пику поглощения электромагнитной энергии, называется областью "аномальной" дисперсии. На участке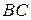 резко убывает с ростом 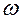. Участку соответствует видимый диапазон 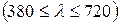нм. Левее точки (К) располагается инфракрасный диапазон (ИК), правее точки (Ф) - ультрафиолетовый (УФ). В увеличенном масштабе участок (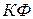) имеет вид, показанный на рисунке 9. 15. Поскольку 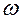~ 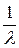, зависимости 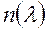соответствует рисунок 9.16, откуда следует, что 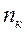для красного и ИК - диапазонов и 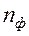- для фиолетового и УФ диапазонов, связаны следующим соотношением

 

.

 

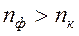В диэлектрических оптических волноводах, ионы которых содержат по нескольку электронов, ход зависимости более сложен (рис. 9.17) и каждая из областей аномальной дисперсии имеет свой пик поглощения. Так например, в "чистом" SiO₂ наибольшие неприятности доставляют 2 типа поглощения: первый расположен в ИК - диапазоне, второй в УФ – области. "Хвосты" от указанных пиков поглощения оставляют для распространения сигнала лишь узкое "окно" прозрачности на длине волны 1,2 мкм с шириной самого " окна" около 0,4 мкм. Именно этот диапазон длин волн сегодня наи­более перспективен при конструировании ВОЛС на основе SiO₂.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. Дисперсия как физическое явление.

2. Физический смысл абсолютного показателя преломления.

3. От каких параметров зависит напряженность поля связанных зарядов в диэлектрике?

4. Обоснуйте дифференциальное уравнение движения валентного электрона под воздействием внешнего электромагнитного поля.

5. Сделайте вывод формулы (9.16).

6. Дайте понятия областей нормальной и аномальной дисперсии.

7. Почему резонансная частота колебаний валентного электрона меньше частоты его собственных колебаний?

8. Изобразите ход зависимости 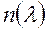для волн видимого диапа­зона.