Проинтегрируем [8, стр. 43] уравнение (2.10) по замкнутой поверхности 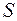 , в левой части (см. рис. 2.3) и по объему
, в левой части (см. рис. 2.3) и по объему  - в правой части уравнения:
- в правой части уравнения:
 . (2.16)
. (2.16)
Уравнение (2.16) отражает смысл теоремы Остроградского-Гаусса:
Поток вектора 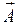 через любую замкнутую поверхность площади
через любую замкнутую поверхность площади 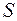 равен интегралу от дивергенции вектора
равен интегралу от дивергенции вектора 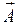 по объему
по объему  , заключенному внутри этой поверхности.
, заключенному внутри этой поверхности.
2.5. ЦИРКУЛШИЯ ВЕКТОРА  ПО КОНТУРУ
ПО КОНТУРУ 
Пусть в некоторой области пространства ( ) задано поле вектора
) задано поле вектора  . Построим в этом пространстве воображаемый замкнутый контур
. Построим в этом пространстве воображаемый замкнутый контур  , рисунок 2.4:
, рисунок 2.4:
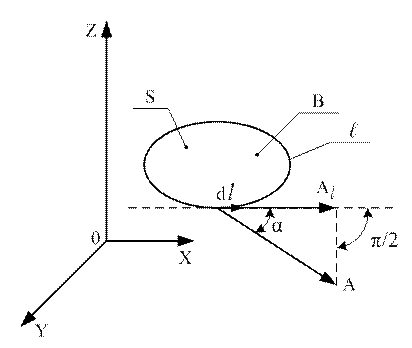
Рисунок 2.4
Спроектируем вектор  на элемент длины контура
на элемент длины контура  . Из рисунка 2.4 видно, что
. Из рисунка 2.4 видно, что 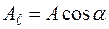 . Считая
. Считая  условным вектором, указывающим направление "обхода" контура
условным вектором, указывающим направление "обхода" контура  , получаем, согласно правила СКАЛЯРНОГО произведения векторов:
, получаем, согласно правила СКАЛЯРНОГО произведения векторов:
 , (2.17)
, (2.17)
Интегрируя (2.17) по замкнутому контуру  , имеем
, имеем
 (2.18)
(2.18)
Выражение (2.18) носит название циркуляции вектора 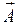 по контуру
по контуру  , [8, стр. 43-46]. Заметим, что по определению,
, [8, стр. 43-46]. Заметим, что по определению,  - СКАЛЯР.
- СКАЛЯР.
РОТОР ВЕКТОРА
Начнем сжимать контур  , уменьшая его размеры, к точке "
, уменьшая его размеры, к точке " 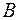 ", (рис. 2.4). Поскольку площадь
", (рис. 2.4). Поскольку площадь 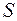 и периметр контура станут убывать, уменьшится и циркуляция
и периметр контура станут убывать, уменьшится и циркуляция  (2.18). При
(2.18). При 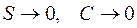 , а их отношение
, а их отношение  будет стремиться к некоторому ПРЕДЕЛУ
будет стремиться к некоторому ПРЕДЕЛУ
 , (2.19)
, (2.19)
который носит название РОТОРА вектора 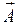 , [8, стр. 46-48].
, [8, стр. 46-48].
Наличие  в точке "
в точке " 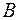 " означает, что в окрестности этой точки существует ПОЛЕ вектора
" означает, что в окрестности этой точки существует ПОЛЕ вектора 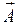 ВИХРЕВОГО типа (рис. 2.5).
ВИХРЕВОГО типа (рис. 2.5).

Рисунок 2.5
Ротор вектора считают ПСЕВДОВЕКТОРОМ, направление которого определяется правилом правого винта и зависит от направления обхода контура (см. направление вектора  на рис. 2.5).
на рис. 2.5).
Если спроецировать контур  на плоскости (
на плоскости (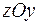 ), (
), (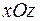 ), (
), ( ) декартовой системы координат (рис. 2.4) можно найти проекции вектора
) декартовой системы координат (рис. 2.4) можно найти проекции вектора  на оси
на оси  .
.
Согласно (2.18), (2.19) и рисунку 2.4:
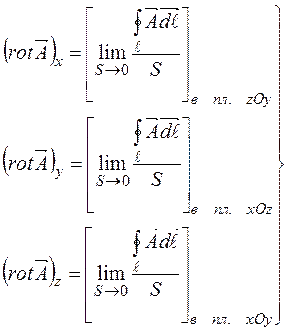 , (2.20)
, (2.20)
Вычисление правых частей уравнений (2.20) [8, стр. 46-48], дает следующие значения проекций РОТОРА вектора 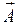 на координатные оси:
на координатные оси:
 , (2.21)
, (2.21)
Из системы уравнений (2.21) и определения ВЕКТОРА следует, что
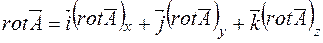 , (2.22)
, (2.22)
Для записи функции  в операторной форме, перемножим векторно НАБЛА-ОПЕРАТОР
в операторной форме, перемножим векторно НАБЛА-ОПЕРАТОР  (2.22) и вектор
(2.22) и вектор
 . (2.23)
. (2.23)
По определению векторного произведения

 .
.
Аналогично:

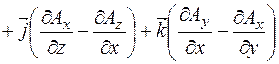 .
.
Согласно (2.21):
 . (2.23)
. (2.23)
Таким образом, в соответствии с (2.23) и (2.22), получаем выражение для функции  в операторной форме:
в операторной форме:
 (2.24)
(2.24)
ТЕОРЕМА СТОКСА
По определению РОТОРА вектора 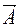 , (формула 2.19), циркуляция
, (формула 2.19), циркуляция 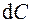 вектора
вектора 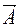 по контуру с площадью
по контуру с площадью  (рис. 2.6) определяется выражением
(рис. 2.6) определяется выражением
 (2.25)
(2.25)
Поскольку в данном случае
 (2.26)
(2.26)
величина  совпадает с его проекцией на единичную нормаль
совпадает с его проекцией на единичную нормаль  к элементарной площадке
к элементарной площадке  . Величина же
. Величина же 
 имеет смысл элементарного потока вектора
имеет смысл элементарного потока вектора  через площадки
через площадки  . На основании (2.26) можно также утверждать, что
. На основании (2.26) можно также утверждать, что

где  определяется формулой (2.5).
определяется формулой (2.5).
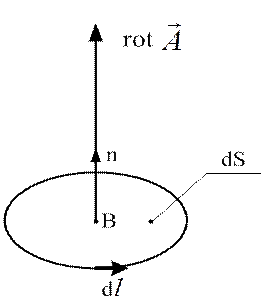
Рисунок 2.6
Действительно:
 (2.27)
(2.27)
поскольку 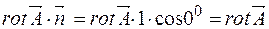 .
.
Из (2.25) и (2.27) следует, что
 . (2.28)
. (2.28)
"Заполним" контур конечных размеров с площадью 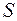 (рис. 2.4) набором множества малых контуров с площадями
(рис. 2.4) набором множества малых контуров с площадями  каждый (рис.2.6).
каждый (рис.2.6).
Интегрируя в левой части уравнения (2.28) от 0 до  , а в правой части от 0 до
, а в правой части от 0 до 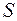 , получим:
, получим:
 (2.29)
(2.29)
Величина С имеет смысл СУММАРНОЙ ЦИРКУЛЯЦИИ вектора 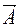 по всей элементарным контурам площади
по всей элементарным контурам площади  , наполняющих контур с площадью
, наполняющих контур с площадью 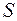 . Известно [8, стр. 48-49], что такая циркуляция НЕ ОТЛИЧАЕТСЯ от циркуляции вектора
. Известно [8, стр. 48-49], что такая циркуляция НЕ ОТЛИЧАЕТСЯ от циркуляции вектора 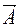 по ПЕРИМЕТРУ КОНТУРА
по ПЕРИМЕТРУ КОНТУРА  (формула (2.18)). Приравнивая левые части (2.18) и (2.29), имеем:
(формула (2.18)). Приравнивая левые части (2.18) и (2.29), имеем:
 (2.30)
(2.30)
Формула (2.30) является математической записью теоремы Стокса [8, стр. 48-49].
Циркуляция вектора 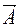 по контуру
по контуру  равна потоку вектора
равна потоку вектора  через произвольную поверхность
через произвольную поверхность 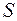 , ограниченную этим контуром.
, ограниченную этим контуром.
ЗАКЛЮЧЕНИЕ по главе 2
Некоторые из полученных результатов сведены в итоговую таблицу 2.1, облегчающую ПОНИМАНИЕ и ЗАПОМИНАНИЕ основных положений теории ПОЛЯ, необходимых для овладения программой курса "ОСНОВЫОПТИКИ".
Таблица 2.1 – Характеристики наиболее употребляемых функций теории поля
| Наимено-вание функции и ее название | Вектор или скаляр | Запись функции в декартовой системе координат | Запись функции в операторной форме | Смысл функции |
1. 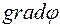 Градиент скалярной функции
Градиент скалярной функции
| ВЕКТОР |

|

| Направление вектора  показывает направление быстрейшего возрастания функции показывает направление быстрейшего возрастания функции 
|
2.  Диверген-ция вектора
Диверген-ция вектора 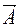
| СКАЛЯР |

|
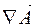
| Характеризует наличие источников или "стоков" векторного поля в пространстве |
3.  РОТОР вектора
РОТОР вектора 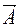
| ВЕКТОР |

|

| В окрестности любой точки пространства, где  существует векторное поле существует векторное поле 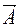 вихревого типа. вихревого типа.
|
КОНТРОЛЬНЫЕ ВОПРОСЫК ГЛАВЕ 2
1. Скалярное произведение векторов.
2. Векторное произведение векторов.
3. Циркуляция вектора по контуру.
4. Поток вектора через элементарную площадку.
5. Векторный дифференциальный оператор Гамильтона.
6. Смысл функций: ГРАДИЕНТ ДИВЕРГЕНЦИЯ РОТОР.
7. Математическая запись функций градиент, дивергенция, ротор в декартовой системе координат и в векторной форме.
8. Теорема ОСТРОГРАДСКОГО – ГАУССА.
9. Теорема СТОКСА.
Глава 3. СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА И ПОНЯТИЕ ОБ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЕ [8, с. 99-312], [9]