2.1. ГРАДИЕНТ СКАЛЯРНОЙ' ФУНКЦИИ [8, стр. 36]
Пусть скалярная функция φ(x, y, z) определена во всем трёхмерном пространстве декартовой системы координат (рис.2.1), и представляет собой одну из изменяющихся физических величин: плотность, температуру, потенциал, относительную диэлектрическую проницаемость, абсолютный показатель преломления и т.д.
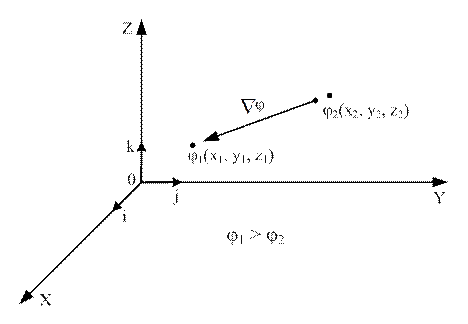
Рисунок 2.1
Изменение φ(x, y, z) в зависимости от координат зададим в виде частных производных
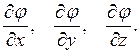
Если 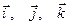 единичные направляющие векторы координатных осей
единичные направляющие векторы координатных осей  , можно ввести вектор [1]
, можно ввести вектор [1]
 (2.1)
(2.1)
который называют ГРАДИЕНТОМ СКАЛЯРНОЙ ФУНКЦИИ φ(x, y, z). Согласно (2.1) производные по x, y, z от φ имеют смысл проекций 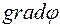 на координатные оси, т.е.:
на координатные оси, т.е.:
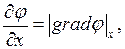
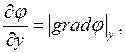
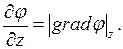
Введем векторный дифференциальный оператор ГАМИЛЬТОНА 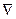 , (то же самое, что НАБЛА - ОПЕРАТОР):
, (то же самое, что НАБЛА - ОПЕРАТОР):
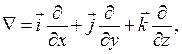 (2.2)
(2.2)
С помощью (2.2) градиент можно представить в операторной форме:
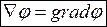 , (2.3)
, (2.3)
Из понятия о градиенте следует, что он характеризует быстроту изменения скалярной функции в зависимости от координат x, y, z. Направление вектора  показывает направление БЫСТРЕЙШЕГО возрастания скалярной функции (
показывает направление БЫСТРЕЙШЕГО возрастания скалярной функции (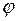 ).
).
ПОТОК ВЕКТОРА
Построим элементарную площадку 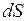 , совмещенную с началом вектора
, совмещенную с началом вектора  (рис. 2.2) [8, стр. 37-40].
(рис. 2.2) [8, стр. 37-40].

Рисунок 2.2
Восстановим к площадке  вектор ЕДИНИЧНОЙ НОРМАЛИ
вектор ЕДИНИЧНОЙ НОРМАЛИ  . Спроецируем
. Спроецируем 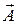 на продолжение
на продолжение  . Согласно рисунку 2.2,
. Согласно рисунку 2.2,
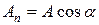 , (2.4)
, (2.4)
Поскольку  - единичный вектор,
- единичный вектор,
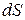 численно =
численно = 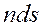
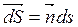 , (2.5)
, (2.5)
где 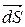 - условный вектор, модуль которого численно равен площади элементарной площадки
- условный вектор, модуль которого численно равен площади элементарной площадки 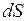 , а направление совпадает с вектором единичной нормали.
, а направление совпадает с вектором единичной нормали.
Умножим 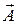 на
на 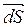 СКАЛЯРНО:
СКАЛЯРНО:
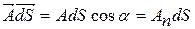 . (2.6)
. (2.6)
Полученное произведение обычно обозначают 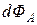 и называют элементарным потоком вектора
и называют элементарным потоком вектора 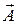 через площадку
через площадку  . Таким образом, из (2.4), (2.5) и (2.6) следует, что элементарный поток вектора
. Таким образом, из (2.4), (2.5) и (2.6) следует, что элементарный поток вектора 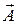 может быть представлен в одной из трех форм записи:
может быть представлен в одной из трех форм записи:
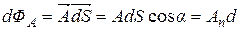 . (2.7)
. (2.7)
Согласно (2.7), поток вектора является скалярной (алгебраической) величиной. Очевидно, что 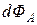 >0, если
>0, если  и
и 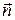 совпадают по направлению (
совпадают по направлению (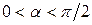 ). Если
). Если  и
и 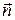 направлены в разные стороны (
направлены в разные стороны (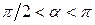 ),
), 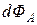 <0. Поток
<0. Поток 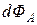 максимален по модулю при
максимален по модулю при 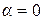 и
и 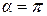 . При
. При 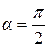 ,
, 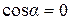 и
и 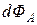 = 0.
= 0.
Заметим, что направление 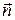 относительно
относительно 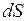 условно
условно
и могло быть выбрано ПРОТИВОПОЛОЖНЫМ тому, которое изображено на рисунке 2.2. Однако для ЗАМКНУТЫХ поверхностей 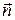 принято строить по направлению ОТ ЦЕНТРА поверхности НАРУЖУ (ортогонально элементарной площадке
принято строить по направлению ОТ ЦЕНТРА поверхности НАРУЖУ (ортогонально элементарной площадке 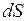 , принадлежащей поверхности). Такие нормали к поверхностям обычно называют "ПОЛОЖИТЕЛЬНЫМИ".
, принадлежащей поверхности). Такие нормали к поверхностям обычно называют "ПОЛОЖИТЕЛЬНЫМИ".
ДИВЕРГЕНЦИЯ ВЕКТОРА
Зададим поле вектора 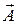 , определенное в любой точке пространства x, y, z, рисунок 2.3.
, определенное в любой точке пространства x, y, z, рисунок 2.3.
Окружим точку " 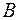 " в пространстве замкнутой воображаемой поверхностью с объемом
" в пространстве замкнутой воображаемой поверхностью с объемом 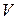 и площадью
и площадью 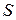 .
.
Элементарный поток вектора 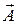 через площадку
через площадку 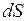 , принадлежащую поверхности
, принадлежащую поверхности 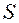 определяется формулой (2.7). Поток вектора
определяется формулой (2.7). Поток вектора 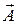 через всю замкнутую поверхность получим интегрированием формулы (2.7); [8, стр. 40-42]:
через всю замкнутую поверхность получим интегрированием формулы (2.7); [8, стр. 40-42]:
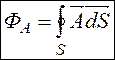 . (2.8)
. (2.8)

Рисунок 2.3
Начнем уменьшать объем 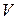 , равномерно "стягивая" его к точке "
, равномерно "стягивая" его к точке " 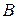 ". Поток
". Поток 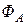 станет убывать, и при
станет убывать, и при 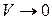 ,
, 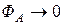 , отношение (
, отношение (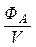 ) будет стремиться к некоторому пределу
) будет стремиться к некоторому пределу
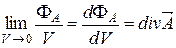 , (2.9)
, (2.9)
который называют ДИВЕРГЕНЦИЕЙ вектора 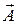 в точке "
в точке " 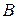 ".
".
Физический смысл дивергенции вектора 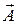 заключается в следующем:
заключается в следующем:
1. Если скалярная функция 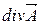 >0, в точке "
>0, в точке " 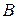 ", рисунок 2.3 существует источник поля вектора
", рисунок 2.3 существует источник поля вектора 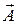 .
.
2. Если 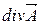 <0, в точке "
<0, в точке " 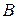 " имеет место "СТОК" векторного поля.
" имеет место "СТОК" векторного поля.
3. При 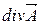 = 0 - в точке "
= 0 - в точке " 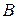 " отсутствуют как источники, так и стоки, поля (либо число источников равно числу идентичных им "стоков").
" отсутствуют как источники, так и стоки, поля (либо число источников равно числу идентичных им "стоков").
Согласно (2.9)
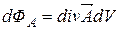 . (2.10)
. (2.10)
В трехмерной системе координат поток 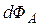 элементарного объема
элементарного объема 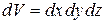 можно представить в виде суммы трех элементарных потоков вдоль осей
можно представить в виде суммы трех элементарных потоков вдоль осей 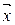 ,
, 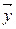 ,
, 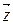 :
:
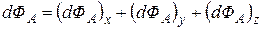 . (2.11)
. (2.11)
Элементарные вычисления слагаемых в правой части равенства (2.11), [8, стр. 40-42] дают следующие значения:
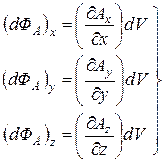 . (2.12)
. (2.12)
Подстановка (2.12) в (2.11) позволяет представить 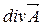 с учетом (2.10) в следующем виде:
с учетом (2.10) в следующем виде:
 , (2.13)
, (2.13)
где  ,
,  ,
, 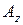 - проекции вектора
- проекции вектора 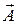 на координатные оси, при условии, что начало вектора
на координатные оси, при условии, что начало вектора 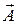 находится в точке "
находится в точке " 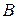 " (рис. 2.3). Перемножим вектор
" (рис. 2.3). Перемножим вектор
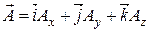
и векторный дифференциальный оператор Гамильтона скалярно.
По правилу скалярного произведения:
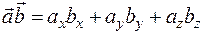 ,
,
следовательно,
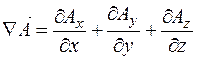 . (2.14)
. (2.14)
Из сравнения (2.13) и (2.14) видно, что дивергенция вектора 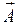 может быть записана в виде:
может быть записана в виде:
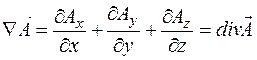 . (2.15)
. (2.15)