Глава 8. ДВУХЛУЧЕВАЯ И МНОГОЛУЧЕВАЯ ИНТЕРФЕРЕНЦИИ

8.1. ДВУХЛУЧЕВАЯ ИНТЕРФЕРЕНЦИЯ, ИНТЕРФЕРОМЕТР МАЙКЕЛЬСОНА [10, с. 134-136]

Большинство оптических схем, в которых используется или исследуется интерференция света, могут быть разделены на две ос­новные категории. Первая из них основана на двулучевой интер­ференции, вторая - на многолучевой. Как было показано в главе 7, одним из необходимых условий получения интерференционного спектра является требование когерентности волн во взаимодействующих световых пучках. Из сказанного об интерференции в главах 6 и 7 следует, что получение когерентных световых пучков от различных (незави­симых) источников света не представляется возможным. Поэтому, све­товые пучки, близкие к когерентным, обычно получают от одного ис­точнике путем искусственного разделения излучения на несколько световых пучков. Примером разделения излучения на два световых пучка могут служить оптические схемы с использованием бипризмы Френеля, схема для получения интерференционных колец Ньютона, схема с зеркалом Ллойда и другие.

После разделения излучения на когерентные световые пучки, они сводятся в одну точку, в которой наблюдается интерференцион­ный максимум или минимум.

В качестве классического примера использования двулучевой интерференции рассмотрим принцип работы интерферометра Майкельсона, оптическая схема которого показана на рисунке 8.1.

Излучение 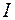от источника 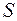входит в светоделительную плоско-параллельную пластину , верхняя поверхность которой 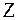покрыта полупрозрачной тонкой пленкой серебра. В точке пласти­чны излучение 1 делится на два световых пучка 2 и 3 равной интенсивности. Световой пучок 2 распространяется по траектории 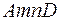и отражается в точке 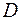от зеркала 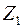. От­раженный световой пучок 2 ' распространяется по траектории , отражается в точке от пластины и распространяется в нап­равлении . 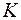Световой пучок 3, отразившись в точке от поверхности пластины , распространяется по траектории 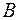и отражается в точке 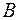от зеркала 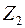. Отраженный световой пучок 3 ' распространяется по траектории 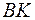, преломляется в пластину и выходит из нее в точке , распространяясь далее в направлении . Пластина 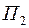, имеющая ту же толщи­ну и сорт стекла, что и пластина и параллельная ей, исполь­зуется для дополнительного выравнивания интенсивностей световых пуч­ков. Из рисунка видно, что .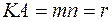

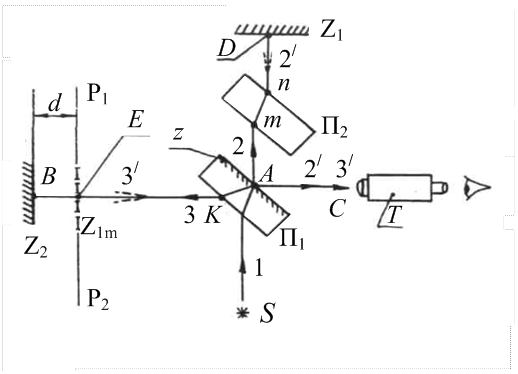
Рисунок 8.1

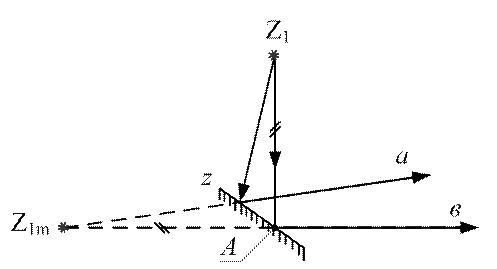
Рисунок 8.2

В результате световой пучок (3+3 ') проходит в стекле путь (), как и пучок (2+2 '). Каждый из пучков испытывает по два отражения от зеркальных поверхностей. В результате пучки 2 ' и 3 ' имеют дос­таточно близкую интенсивность и достаточно когерентны между со­бой для того, чтобы интерферировать, поскольку получены от од­ного источника . Для наблюдения интерференционной картины используется зрительная труба .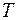

Найдем область локализации интерференционного спектра.
Представим себе, что световые лучи от источника 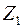отражаются
зеркалом 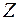и распространяются в направлениях (а) и (в) (рис. 8.2).

Как видно из рисунка 8.2, в точке располагается мнимое изображение источника 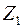. Сравнивая рисунок 8.1 с рисунком 8.2, заме­чаем, что (рис. 8.1) есть мнимое изображение зеркала 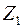, в полупрозрачной отражающей поверхности пластины . Раз­ность оптических длин путей световых пучков (3+3 ') и (2+2 ') определяется разностью длин траекторий

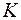
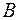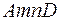- . (8.1)

Из рисунков 8.1 и 8.2 следует, что

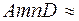
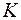
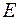. (8.2)

Подставляя (8.2) в (8.1), имеем

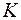
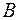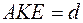- . (8.3)

Величину называют разностью длин плеч интерферометра. Из приведенного рассуждения следует, что интерференционную картину можно считать локализованной в плоскости 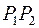, совпадаю­щей с плоскостью мнимого изображения зеркала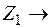 (рис. 8.1). Поэтому схему рис. 8.1 можно заменить эквивалентной схемой, пока­занной на рис. 8.3.

Световой пучок 3, изображенный на рис. 8.1 фактически пред­ставляет собой световой конус с углом раскрытия 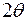, показан­ный на эквивалентной оптической схеме (рис. 8.3), который отражает­ся от зеркала 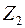и распространяется в виде конуса с образующи­ми 3 '. При прохождении лучей 3 ' через точки 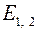,всегда найдется "луч" 2, параллельный лучу 3, который отразившись от "зеркала" пойдет по направлению 3 '. Волны, соответствую­щие лучу 3 ' и лучу 2 ' (после его отражения в точке 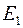) будут интерферировать в плоскости 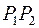, которой принадлежит точка 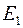. В результате интерференции, в точке 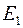будет иметь место максимум (или минимум), который наблюдается в зрительную трубу (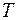), согласно рисунку 8.1. Аналогичный максимум (или минимум) будет наблю­даться в точке 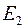, симметричной относительно 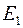и отстоящей от центра интерференционной картины на расстояние 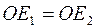(pиc. 8.3).

Для нахождения аналитических условий для максимумов и ми­нимумов, изобразим участок 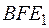рисунка 8.3 в увеличенном виде на рис. 8.4. Согласно рисунку 8.4, оптическая разность xoдa между волнами 3 и 2 начинается в сечении 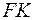и заканчивается в точке 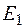после отражения волны 2 от "зеркала" .

Рисунок 8.3

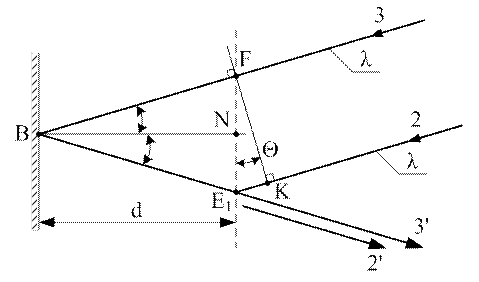
Рисунок 8.4

Величина этой разности составляет

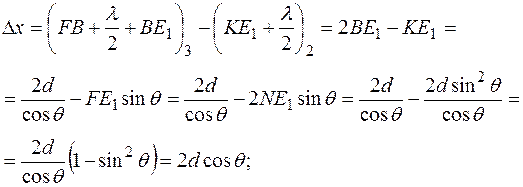
Таким образом,

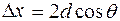. (8.4)

Условие интерференционных максимумов:

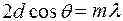. (8.5)

Условие минимумов:

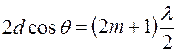, (8.6)

.

Выражения (8.5) и (8.6) определяют положение максимумов и минимумов не только в точках 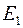, 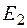как показано на рисунке 8.3, но и во всей плоскости 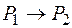, ортогональной оси симметрии (рис. 8.3). В результате, интерференционная картина имеет форму системы концентричес­ких колец с центром в точке . Такой интерференционный спектр называют системой полос равного наклона, поскольку его форма при 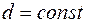зависит только от угла . Заметим, что системе полос равного наклона в интерферометре Майкельсона должна соответствовать строгая ортогональность плоскости зеркал и 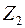и, следовательно, строгая параллельность зеркала 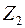мнимому зерка­лу (рис. 8.1).

Если лучи световых пучков 3 и 2 идеально параллельны, а поверхность зеркал и 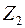неортогональна на несколько угловых секунд, зеркало 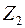и мнимое зеркало образуют клин с малым углом и величина вдоль этого клина плавно изменяется. В этом случае интерференционная картина имеет форму параллельных полос, которые называют полосами равной толщины.

Если лучи пучков 2 и 3 идеально параллельны, а зеркала и 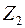, строго ортогональны, согласно (8.5) и (8.6) в зрительной трубе 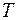(рис. 8.1) будет наблюдаться либо одно светлое пятно, либо одно темное. В этом случае 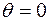, и для максимума

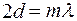. (8.7)

а для минимума

, (8.8)

Переход от максимума к минимуму можно осуществить плавным изме­нением разности длин плеч интерферометра .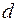

Аналогичный принцип двулучевой интерференции используется в конструкции интерферометров Жамена, Рождественского [11 с. 174-181] и других, аналогичных им. Двулучевые интерферометры как измери­тельные приборы обычно используются для определения линейных раз­меров, длин электромагнитных волн, абсолютных показателей прелом­ления, качества обработки поверхностей.

Из сказанного в 8.1 следует, что под термином "двулучевая интерференция", который сложился исторически, следует понимать интерференцию электромагнитных волн, близких к когерентным, распространяющихся в двух световых пучках, полученных от одного и того же излучателя. Аналогично, термин "многолучевая" интерфе­ренция" подразумевает интерференцию волн, распространяющихся во многих световых пучках, полученных от одного источника.