КОГЕРЕНТНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

 

Две волны называются когерентными, если они имеют одинаковые частоты и неизменяющуюся со временем раз­ность фаз.

 

Пусть одна из волн задана в виде

 

, (5.13)

другая –

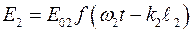. (5.14)

 

По введенному выше определению, волны 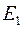и , когерентны, если

 

, (5.15)

 

. (5.16)

 

В однородной изотропной среде фазовые скорости волн

 

.

 

Поскольку

 

, .

 

Выражение (5.16) для разности фаз упрощается, и

 

. (5.17)

 

В результате, условие когерентности волн с учетом (5.13 - 5.17) принимает вид

 

, (5.18)

 

, (5.19)

 

. (5.20)

 

Для практических расчетов разности фаз (5.20). Возможны 2 способа:

 

1) Если - "оптическая" разность хода волн,

 

, (5.21)

 

где - длина электромагнитной волны в вакууме.

 

2) Если - геометрическая разность хода волн,

 

, (5.22)

 

где 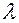- длина волны в диэлектрике.

Нетрудно убедиться в том, что расчет по формулам (5.21) и
(5.22) дает один и тот же результат.

В вакууме:

 

, (5.23)

 

В диэлектрике

 

. (5.24)

 

Разделив (5.23) на (5.24) почленно, получим

 

,

 

, (5.25)

 

. (5.26)

 

Таким образом, в диэлектрике длина волны изменяется в раз по сравнению с ее длиной в вакууме.

Подставляя (5.26) в (5.22) и учитывая (5.12), имеем:

 

.

 

 

5.4. ЛИНЕЙН0-П0ЛЯРИ30ВАННАЯ ЭЛЕКТРОМАРНИТНАЯ ВОЛНА [8, с. 428]

 

Волна называется линейно поляризованной, если в процессе ее распространения в пространстве вектор напряженности (или ) остаётся параллель­ным самому себе.

 

5.5. ИНТЕРФЕРЕНЦИЯ КОГЕРЕНТНЫХ МОНОХРОМАТИЧЕСКИХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН, РАСПРОСТРАНЯЮЩИХСЯ В ОДНОРОД­НОЙ, ИЗОТРОПНОЙ ДИЭЛЕКТРИЧЕСКОЙ СРЕДЕ

 

Пусть генератор 1 (рис. 5.3) излучает плоскую волну

 

, (5.27)

 

поляризованную вдоль оси () и распространяющуюся вдоль оси (). Генератор 2 излучает плоскую волну

 

, (5.28)

 

поляризованную вдоль оси () и распространяющуюся вдоль оси (). В точке волны встречаются, колебания векторов складываются, либо усиливая, либо ослабляя результирующее поле .

Процесс сложения колебаний векторов напря­женности электрического поля в среде, вызван­ный прохождением через рассматриваемую сре­ду двух или более когерентных электромагнит­ных волн называется ИНТЕРФЕРЕНЦИЕЙ.

Рисунок 5.3

 

Из рисунка 5.3, видно, что максимальное усиление результирующего поля в точке 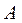будет в том случае (рис. 5.4), когда разность фаз волн

 

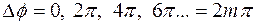
, (5.29)

 

где .

Рисунок 5.4 Рисунок 5.5

Из (5.27) и (5.28)

 

. (5.30)

 

Из (5.29) и (5.30)

 

,

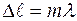или . (5.31)

 

Из (5.29) и (5.31) следует, что

две когерентные волны максимально усиливают резуль­тирующее поле если их разность фаз равна ну­лю или чётному числу радиан, , а разность хода волн равна четному числу полуволн , где

 

Из рисунков 5.3 и 5.5 следует, что максимальное ослабление поля будет в том случае, когда разность фаз волн

 

. (5.32)

 

Из (5.32) и (5.30):

 

,

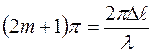. (5.33)

 

Из (5.29) и (5.31) следует, что

 

результирующее поле двух когерентных волн мак­симально ослаблено, если разность их фаз равна не­чётному числу радиан 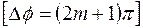, а разность хода равна нечетному числу полуволн, а разность хода волн равна нечетному числу полуволн , .

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫК ГЛАВЕ 5

 

1. Вывод взаимосвязи с и с .

2. Вывод взаимосвязи оптической длины пути с геометрической.

3. Вывод взаимосвязи длины волны в вакууме с ее длиной в диэлектрике.

4. Понятие когерентных волн.

5. Понятие о линейно-поляризованной волне.

6. Вывод условий усиления и ослабления результирующего электри­ческого поля при интерференции когерентных волн.

 

 

Глава 6. ОТЛИЧИЕ РЕАЛЬНОГО ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ ОТ ИДЕАЛЬНОЙ МОНОХРОМАТИЧЕСКОЙ ВОЛНЫ