Как было показано в главе 4, идеальная монохроматическая электромагнитная волна, описываемая уравнениями (4.12, 4.14, 4.18) подразумевает наличие бесконечного во времени и пространстве электромагнитного излучения. Такая идеализированная модель не соответствует реальному оптическому излучению в видимом, ультрафиолетовом, инфракрасном диапазоне. В частности, именно из фотонов инфракрасного диапазона формируется излучение для стекловолокон с несущими частотами (1,5 ÷ 3,5) 10 14 Гц.
В качестве основных факторов, обуславливающих отличие идеальной монохроматической электромагнитной волны от реального оптического излучения, можно привести следующие постулаты Бора:
1) В основе оптического излучения лежит появление фотона частоты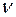 
и энергии 
, возникающее при переходе валентного электрона в атоме или ионе с более высоколежащего энергетического уровня 
на более низкорасположенный 
.
2) По закону сохранения энергии частота фотона
,
где 
- постоянная Планка.
3) Поскольку время излучения фотона 
конечно и составляет величину порядка 10 -8 с, с фотоном связано электромагнитное излучение с длиной волны 
, ограниченное и во времени и в пространстве.
4) Закон изменения напряженности электрического поля 
, распространяющейся волны, периодичен не во всей области её существования как во времени, так и в пространстве.
5) За время излучается не единственный фотон, а множество и, в том числе с близкими частотами 
, которые формируют волновой пакет.
6) Волновые векторы внутри волнового пакета не совпадают полностью ни по величине, ни по направлению. По этой причине группа волн внутри волнового пакета представляет собой излучение отличающееся от идеально плоской волны.
|
|
ГРУППОВАЯ СКОРОСТЬ ВОЛНОВОГО ПАКЕТА
Пусть в простейшем случае волновой пакет состоит из двух гармонических волн с близкими частотами 
и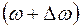 
одной линейной поляризации:
(6.1)
(6.2)
Обозначим 
, 
, согласно (6.1), (6.2) находим результирующую напряженность поля в волновом пакете в виде:
Поскольку, 
, 
,
(6.3)
Уравнение (6.3) показывает, что внутри волнового пакета в процессе его распространения происходят биения результирующего вектора напряженности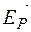 
с частотой (~ 
). Скорость перемещения волнового пакета в пространстве есть скорость передачи его энергии, или скорость распространения биений вектора 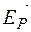. Для нахождения, этой скорости "зафиксируем" фазу биений
,
и продифференцируем ее по времени (подобно тому как мы нашли фазовую скорость 
в 4.7:
. (6.4)
Согласно (6.4) приближённое значение групповой скорости
.
Точное значение групповой скорости
. (6.5)
При нахождении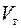 
мы допустили, что волны (1) и (2) - гармонические.
Если 
и 
переменные периодические функции, произвольно изменяющиеся в зависимости от 
и 
, они могут быть разложены на бесчисленное множество гармонических составляющих с близкими частотами [8 с. 355]. Выполняя попарно сложение таких составляющих, мы получим тот же результат (6.5).