6.1 Принятие решений в условиях риска
Особенностью принятия решений в условиях риска состоит в том, что наступление определенных условий внешней среды ожидается с определенной вероятностью. Значения этой вероятности могут быть определены либо объективно на основании статистики или пробных испытаний, либо субъективно. Во всяком случае, эти вероятности известны.
Основой принятия решения в данных условиях является метод матрицы решений, описанный ранее. Следует напомнить, что в матрице отражаются объективные условия (неуправляемы факторы) через Yj, варианты решений через Rj, а также ожидаемый результат при каждом сочетании объективных условий и вариантов решения - через Оij.

| Y1 | Y2 | Y3 |
| R1 | O11 | O12 | O13 |
| R2 | O21 | O22 | O23 |
| R3 | O31 | O32 | O33 |
| R4 | O41 | O42 | O43 |
Теорией и практикой принятия управленческих решений выработаны ряд правил, позволяющий осуществить выбор альтернативы в условиях риска.
Первое из них это правило модального значения (аксиома рациональности). В соответствии с ним учитываются только те результаты, вероятность появления которых максимальна. Это правило называют также аксиомой рациональности, поскольку при единичном выборе представляется разумным предполагать, что именно событие, имеющее максимальную вероятность появления, и наступит. Такой подход в большинстве случаев будет приводить к положительному результату. Однако он имеет и определенные недостатки. Например, он сталкивается с трудностями, когда:
-ряд состояний имеют равную вероятность появления;
-максимальный результат дают несколько альтернатив;
-вероятность появления модального значения при одном из состояний среды только незначительно выше, чем для других состояний среды, при этом другие альтернативы оказываются более оптимальными, иногда значительно[20].
| Состояние среды | Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | Р7 | Р8 | Р9 | Р10 |
| Вероятность появления | 0,14 | 0,10 | 0,06 | 0,08 | 0,07 | 0,15 | 0,13 | 0,12 | 0,07 | 0,08 |
| А1 | ||||||||||
| А2 | 5 | |||||||||
| А3 |
Так, состояние среды Р6 имеет наибольшую вероятность 0,15, и согласно правилу должна быть выбрана альтернатива А1, дающая результат, равный 6. Однако состояние среды Р1, имеющее незначительно меньшую вероятность появления 0,14, для альтернатив А2 и А3 дает заметно лучший результат. Поэтому целесообразность выбора альтернативы А1 может вызывать сомнения.
Второе правило именуется правилом Байеса. Оно в отличие от предыдущего вовлекает в процесс выбора решения все имеющиеся значения. Для этого результат каждой альтернативы для каждого состояния среды умножается на вероятность ее появления.

Здесь ркj- вероятность реализации к-го варианта ситуации.
Например, для альтернативы А1 в указанной выше таблице сумма математических ожиданий будет равна 5,41 (jА1=0,14*5+0,10*4+0,06*4+0,08*5+0,07*1+0,15*6+0,13*8+0,12*6+0,07*10+0,08*3= 5,41); jА2 = 7,05; jА3= 6,25. Оптимальный вариант в данном случае А2, имеющий максимальное математическое ожидание.
Однако и правило Байеса при формальном применении может таить в себе опасность. В следующей таблице приведен пример, когда и по правилу модального значения (при Р2 имеем максимальный результат), и в соответствии с правилом Байеса (сумма равна +6) выбор падает на альтернативу А1.
| Состояние среды | Р1 | Р2 | Сумма |
| Вероятность | 0,4 | 0,6 | |
| А1 | -600 | +410 | +6 |
| А2 | -10 | +15 | +5 |
При неоднократном выборе это решение было бы действительно оптимальным, но при однократном выборе альтернатива А1 может оказаться убийственной, если реализуется значение среды Р1. Следующего выбора, который позволил бы в конечном счете выиграть, может просто не быть из-за банкротства в результате первого выбора.
Поэтому для исключения подобного варианта применяется критерий среднего значения и стандартного отклонения. Для оценки рассеяния значений критерия (выбранного параметра) относительно его среднего прогнозируемого значения математического ожидания целесообразно использовать такую характеристику, стандартное отклонений (среднеквадратичное отклонение). Критерий применяется для учета отношения к риску. Для этого помимо математического ожидания рассчитывают стандартное отклонение результатов. Чем выше стандартное отклонение, тем больше риск. Полезность альтернативных решений (риска) зависит от математического ожидания и стандартного отклонения. Эта зависимость может быть отражена функцией приоритетности риска, которая характеризует отношение лица, принимающего решение, к риску. При боязни риска лицо, принимающее решение, выбирает из двух альтернатив с одинаковыми математическими ожиданиями ту, которая имеет наименьшее стандартное отклонение.
Стандартное отклонение высчитывается по формуле:
 , где
, где
x – ожидаемый результат;
 – среднее значение показателя;
– среднее значение показателя;
n – количество значений в анализируемой совокупности данных.
Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не n, а n- 1:
 .
.
В приведенном примере стандартные отклонения А1 и А2:
| Состояние среды | Р1 | Р2 | Сумма | δ |
| Вероятность | 0,4 | 0,6 | ||
| А1 | -600 | +410 | +6 | 714,18 |
| А2 | -10 | +15 | +5 | 17,68 |
Третье правило - правило Бернулли достаточно широко используется для принятия экономических решений в условиях риска. Оно отличается от правила Байеса тем, что вводится индивидуальная функция полезности. При этом каждое значение в таблице вначале умножается на соответствующее значение функции полезности и уж затем на вероятность соответствующего состояния среды. Далее для каждой альтернативы производится суммирование по всем состояниям среды. Максимальная сумма определяет лучшую альтернативу.
Преимущество этого подхода заключается в учете индивидуальных предпочтений лица принимающего решения. Недостаток правила связан с тем, что функция полезности должна быть определена настолько точно, чтобы быть справедливой для лица принимающего решения и в других ситуациях, и должна быть стабильна во времени, т.е. должна быть применима для конкретных ситуаций и в другое время.
Сущность правила Бернулли можно показать на простейшем бытовом примере. Уходя на работу вы задумываетесь: брать с собой зонт или нет. Возможность дождя от вас не зависит - это объективные условия внешней среды. Возможны два варианта решений: взять зонт (а1) и не брать зонт (а2). На ваш выбор повлияют внешние условия: пойдет дождь (у1) или не пойдет (у2). Допустим, вы считаете, что вероятность дождя Ру1 = 0,5, тогда вероятность хорошей погоды 1- 0,5 = 0,5 (Ру2 =1- Ру1).
Далее необходимо дать оценку потерь (неудобств), которые можно иметь по вариантам возможных решений и влияния погодных условий. Это оценка у разных людей может быть различной (в данном случае в зависимости от отношения индивидуума к дождю и сохранению своей одежды). Но у большинства людей существует какое-то среднее мнение. При решении сложных проблем на данном этапе может быть использован метод экспертных оценок возможных потерь.
В нашем случае примем следующую оценку. По варианту а1 (взять зонт) оценка будет равна 1 (а11), если дождь пойдет, и 2 (а12), если дождя не будет. Это означает, что во время кратковременного пребывания на улице дождя не будет и неудобство носить зонт оценивается единицей, а если вообще дождь не пойдет, то неудобство увеличится вдвое.
По варианту а2 соответственно возможны два события:
дождь пойдет а21 - оценивается числом 6 (опасность испортить одежду, прическу во время дождя при отсутствии зонта) и а22 = 0 - при отсутствии зонта и дождя.
Составим таблицу потерь на основе рассуждений и принятых оценок:
| Линия поведения | Объективные условия | |
| дождь (у1) | нет дождя (у2) | |
| взять зонт (а1) | 1 (а11) | 2 (а12) |
| не брать зонт (а2) | 6 (а21) | 0 (а22) |
Далее определим математическое ожидание потерь при выборе альтернативных линий поведения. Так как математическое ожидание (Е) случайной величины равно Ex = ΣPjXj, то в нашем случае, при вероятности Р= 0,5, для а1 и а2 оно будет равно соответственно:
Ea1 = 0,5 *1+0,5*2= 1,5
Еа2= 0,5*6+0,5*0=3,0
Чтобы минимизировать возможные потери, в нашем примере необходимо остановить выбор на линии поведения а1, то есть взять зонт[21].
6.2. Принятие решений в условиях неопределенности
Принятие решения в условиях неопределенности имеет место, когда то или иное действие (или все действия) приводит к множеству возможных исходов, вероятности которых неизвестны.
Нередко результат решения зависит от наступления определенных внешних ситуаций, которые не только не контролируются, но и по которым у него отсутствует информация, при какой из этих ситуаций его решение должно быть эффективным. Особая трудность появляется, когда при конкретных внешних ситуациях каждый раз оптимальной была бы другая альтернатива. Выбор решения в таких условиях и называют принятием решения в условиях неопределенности.
Теорией управления и принятия решений были разработаны ряд критериев, позволяющие принять решение в условиях неопределенности. Но прежде чем их описать следует упомянуть, что, также как и в ситуациях с риском, основой принятия решения в условиях неопределенности является метод матрицы решений, которая предварительно составляется самым тщательным образом.
1. Критерий Вальда (максиминный) - наибольшая осторожность («рассчитывай на худшее»).
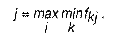
2. Критерий Лапласа - «ориентируйся на среднее»

3. Критерий крайнего оптимизма (максимаксный) - «верь в удачу»

4. Критерий максимального сожаления - «меньше сожаления в будущем» (критерий Сэвиджа)

Следует отметить, что для применения критерия Сэвиджа необходимо предварительно построить матрицу сожаления, в ячейках которой записывается разница между максимальным результатом при данном исходе (максимальном числе в данном столбце) и результатом при выбранной стратегии. Далее для каждой стратегии (в каждой строке) ищут максимальную величину сожаления. И выбирают то решение (строку), максимальное сожаление которого минимально.
5. Критерий Гурвица - «компромисс»

где a выбирается из интервала между 0 и 1. Если результаты представляют собой потери, то в последнем критерии  заменяется на
заменяется на  .
.
Коэффициент a является как бы мерой оптимизма лица, принимающего решение. Его выбор субъективен и зависит от темперамента и личной оценки ситуации индивидуумом. Если a близок к 1, то значение критерия Гурвица стремится к значению критерия Вальда. При a близком к 0 значение приближается к значению критерия "крайнего оптимизма"  . Часто a выбирается равным 1/2.
. Часто a выбирается равным 1/2.
[1]Юкаева В.С. Управленческие решения: учебное пособие. М.:Дашков и К° 2009.
[2] На самом деле логические аргументы в данном случае достаточно просты, но если попытаться их строго доказать, то они займут несколько страниц.
[3] Cody R.P., Smith J.K. Applied statistics and the SAS programming Language. Prentice-Hall, Inc., 1991. 445 Pages.
[4] Рылов В.П. Разработка управленческого решения: Учеб.пособие. Омск: Изд-во ОмГТУ, 2009.
[5] Морозова Л.А. Теория государства и права. М.: Юристъ, 2002. — 414 с
[6]Фурта С.Д., Соломатина Т.Б. Карта заинтересованных сторон – инструмент анализа окружения бизнеса // Инициативы XXI века. –№ 1. – 2010. – С.17-22.
[7] Забродская С.А. Отдельные вопросы экономики для студентов и школьников. https://www.ekonomika-st.ru/drugie/metodi/metodi-prognoz-1-1.html (дата обращения: 01.02.2014).
[8] Новикова Н.В., Поздеева О.Г. Прогнозирование национальной экономики: Учебно-методическое пособие. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2007. -137 с.
[9] Громова Н.М., Громова Н.И. Основы экономического прогнозирования. М.:"Академия Естествознания", 2006. URL: https://www.rae.ru/monographs/10 (дата обращения: 27.01.14)
[10]Юкаева В.С. Управленческие решения: учебное пособие. М.:Дашков и К° 2009.
[11] Забродская С.А. Отдельные вопросы экономики для студентов и школьников. https://www.ekonomika-st.ru/drugie/metodi/metodi-prognoz-1-4.html (дата обращения: 01.02.2014).
[12]Дульзон. А.А. Разработка управленческих решений: учебник. Томск: Изд-во Томского политехнического университета, 2009.
[13] Литвак Б.Г. Разработка управленческого решения. М.: Дело, 2008. 439 с.
[14]Виханский О.С. Стратегическое управление: Учебник. М.: Гардарика, 2002.
[15]Юкаева В.С. Управленческие решения: учебное пособие. М.:Дашков и К° 2009.
[16]Дульзон. А.А. Разработка управленческих решений: учебник. Томск: Изд-во Томского политехнического университета, 2009.
[17]Майснер Т.В. Анализ причин неудовлетворительного рейтинга студентов с применением диаграммы Исикавы и предложения по совершенствованию балльно-рейтинговой системы. URL: https://uk.utmn.ru/sec/88 (дата обращения 21.03.2013).
[18] Дульзон. А.А. Разработка управленческих решений: учебник. Томск: Изд-во Томского политехнического университета, 2009.
[19]Юкаева В.С. Управленческие решения: учебное пособие. М.:Дашков и К° 2009.
[20] Дульзон. А.А. Разработка управленческих решений: учебник. Томск: Изд-во Томского политехнического университета, 2009.
[21] Юкаева В.С. Управленческие решения: учебное пособие. М.:Дашков и К° 2009.