Выполнение операций над матрицами.
Вычисление определителей
Цель работы: научиться выполнять сложение, умножение матриц, вычисление определителей.
Ход работы:
(задания согласно вариантам)
1. Выполнить сложение матриц
2. Выполнить умножение матриц
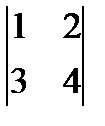
3. Вычислить определитель матрицы второго порядка
4. Вычислить определитель матрицы третьего порядка
Пример ВЫПОЛНЕНия заданий
1. выполнить сложение матриц

2. выполнить умножение матриц

3. вычислить определитель матрицы второго порядка
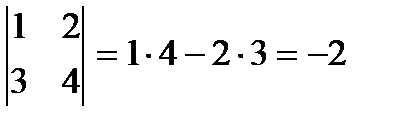
4. вычислить определитель матрицы третьего порядка разложением по первой строке, так как в первой строке содержится 0 (можно было разложить и по второму столбцу, так как в нем также содержится нулевой элемент)
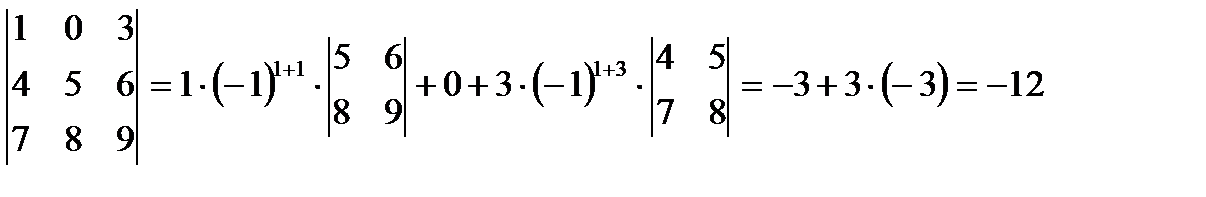
1 вариант
1) 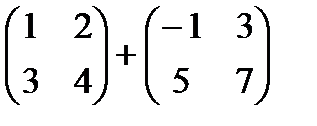 1)
1) 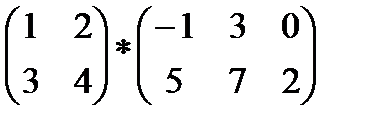 1)
1)  1)
1) 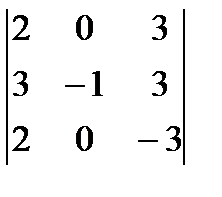
| 9 вариант
1) 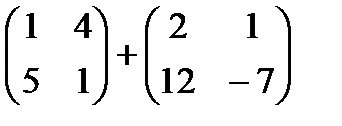 2)
2) 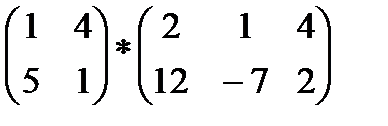 3)
3) 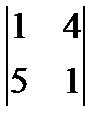 4)
4) 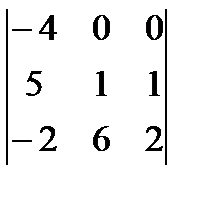
|
2 вариант
1)  2)
2) 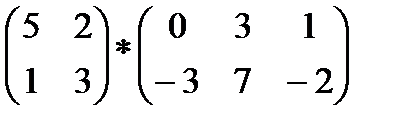 3)
3) 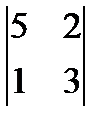 4)
4) 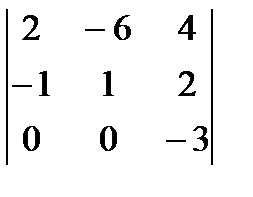
| 10 вариант
1)  2)
2) 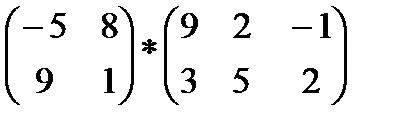 3)
3) 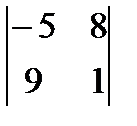 4)
4) 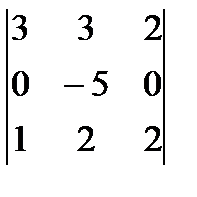
|
3 вариант
1) 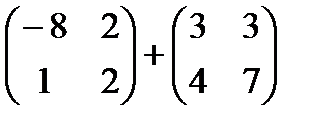 2)
2) 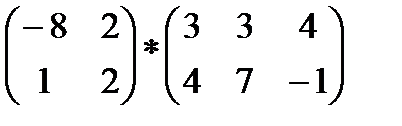 3)
3) 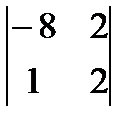 4)
4) 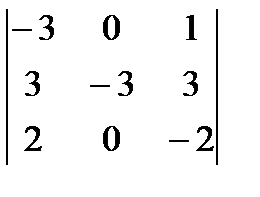
| 11 вариант
1)  2)
2) 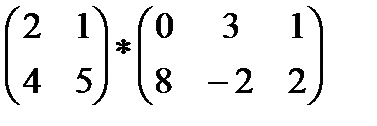 3)
3)  4)
4) 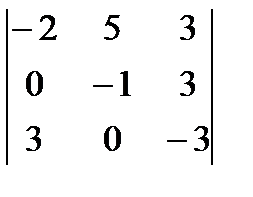
|
4 вариант
1) 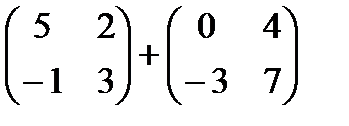 2)
2) 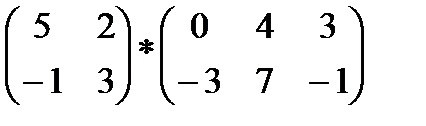 3)
3) 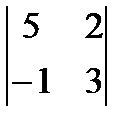 4)
4) 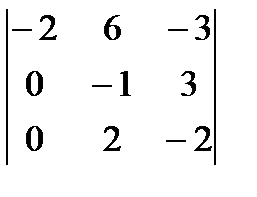
| 12 вариант
1) 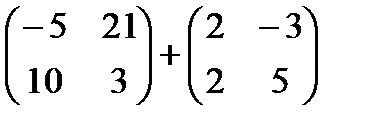 2)
2) 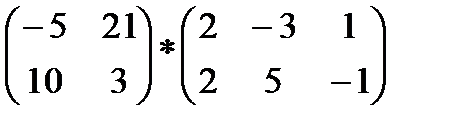 3)
3) 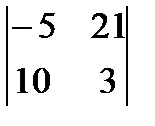 4)
4) 
|
5 вариант
1) 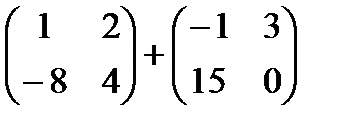 2)
2)  3)
3) 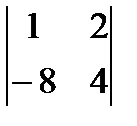 4)
4) 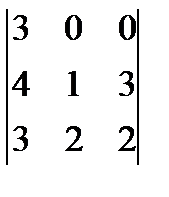
| 13 вариант
1) 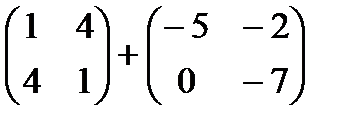 2)
2) 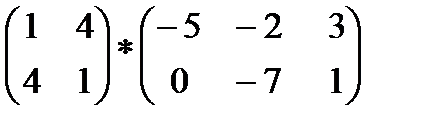 3)
3) 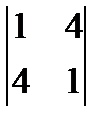 4)
4) 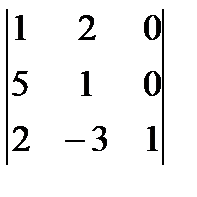
|
6 вариант
1)  2)
2) 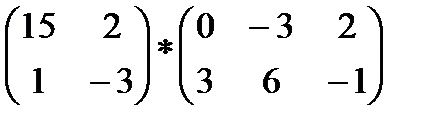 3)
3) 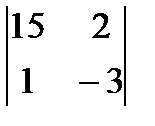 4)
4) 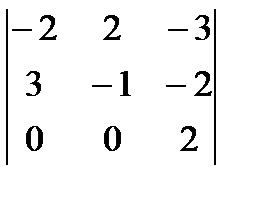
| 14 вариант
1) 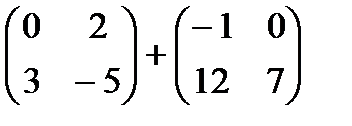 2)
2) 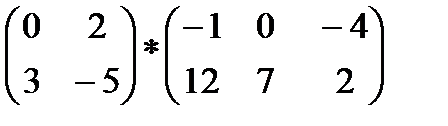 3)
3) 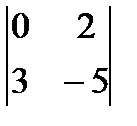 4)
4) 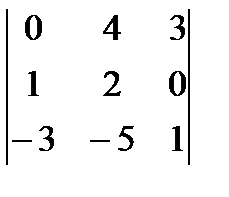
|
7 вариант
1) 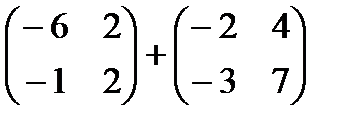 2)
2)  3)
3) 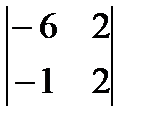 4)
4) 
| 15 вариант
1) 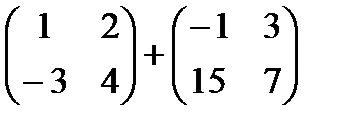 2)
2) 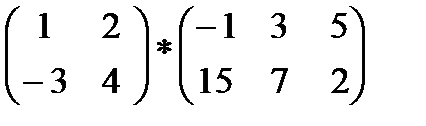 3)
3)  4)
4) 
|
8 вариант
1) 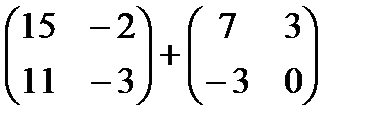 2)
2)  3)
3) 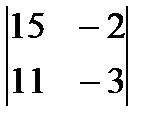 4)
4) 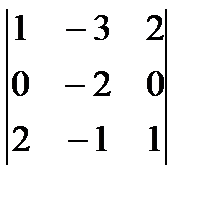
|
Контрольные вопросы:
1. Дайте определение матрицы, размерности матрицы, определителя и порядка определителя. Приведите примеры.
2. Дайте определение квадратной матрицы, диагональной матрицы, ступенчатой матрицы, единичной матрицы.
3. Дайте определение алгебраического элемента матрицы. Приведите формулу для вычисления алгебраического дополнения.
4. Перечислите возможные действия над матрицами.
5. Назовите способы вычисления определителя третьего порядка.
Решение систем линейных уравнений
Цель работы: научиться решать системы линейных уравнений методами Крамера и Гаусса.
Ход работы:
(согласно вариантам)
1. Решить систему линейных уравнений методом Крамера
2. Решить систему линейных уравнений методом Гаусса
Пример ВЫПОЛНЕНия заданий
Найти решение системы линейных уравнений методом Гаусса и методом Крамера.
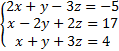
Решим СЛУ методом Крамера:
Найдем основной определитель, составленный из коэффициентов при x, y, z:
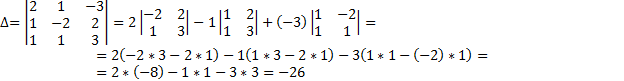
Чтобы найти 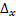 ,
, 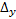 ,
,  , Заменяем в основном определителе соответствующие столбцы на столбец свободных членов (для х первый столбец, для у второй столбец, для z третий столбец):
, Заменяем в основном определителе соответствующие столбцы на столбец свободных членов (для х первый столбец, для у второй столбец, для z третий столбец):
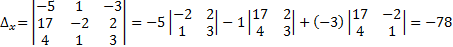
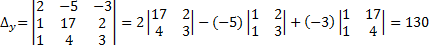

Найдем решение системы по формулам Крамера:
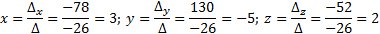
Решим СЛУ методом Гаусса. Для этого почленно умножаем каждое уравнение системы на необходимый коэффициент и складываем попарно уравнения:
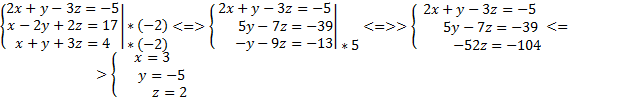
1 вариант
№1. 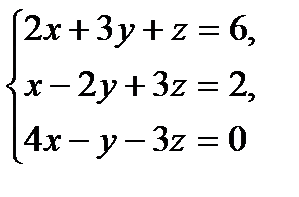 №2.
№2. 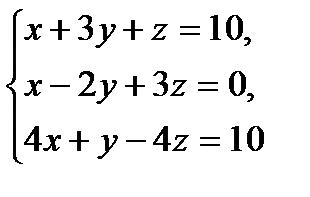
| 4 вариант
№1. 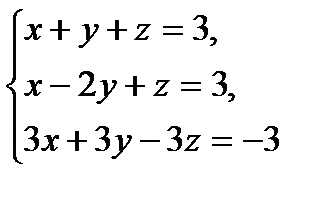 №2.
№2. 
|
2 вариант
№1. 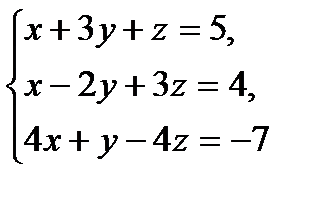 №2.
№2. 
| 5 вариант
№1. 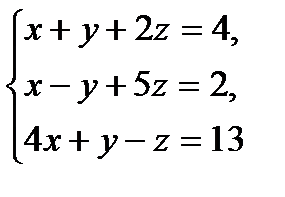 №2.
№2. 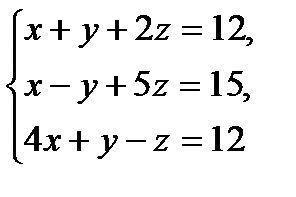
|
3 вариант
№1. 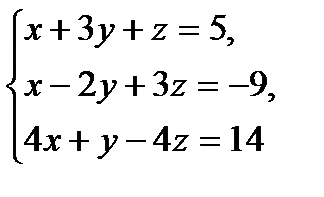 №2.
№2. 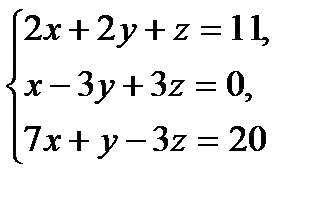
| 6 вариант
№1 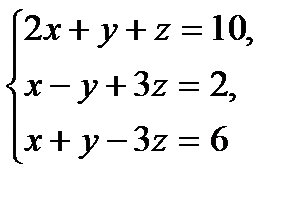 №2.
№2. 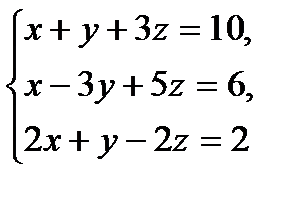
|
7 вариант
№1. 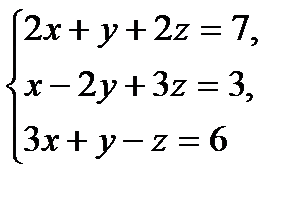 №2.
№2. 
| 12 вариант
№1. 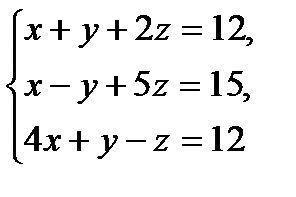 №2.
№2. 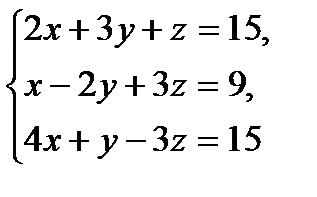
|
8 вариант
№1. 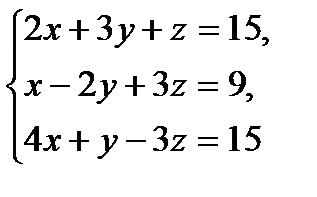 №2.
№2. 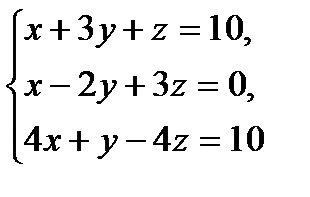
| 13 вариант
№1.  №2.
№2. 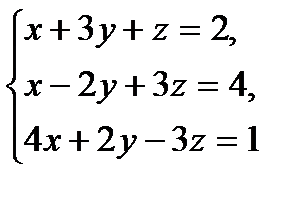
|
9 вариант
№1.  №2.
№2. 
| 14 вариант
№1.  №2.
№2. 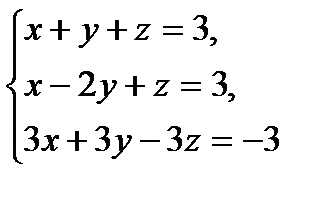
|
10 вариант
№1. 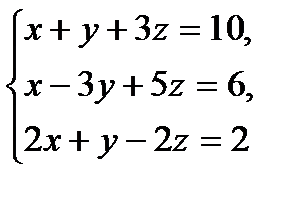 №2.
№2. 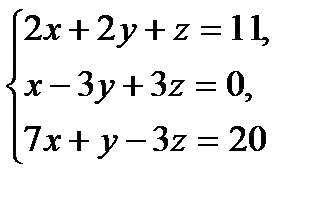
| 15 вариант
№1.  №2.
№2. 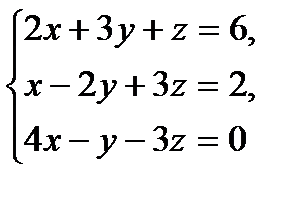
|
11 вариант
№1. 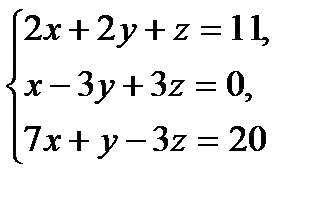 №2.
№2. 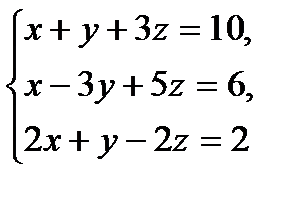
|
Контрольные вопросы:
1. Запишите формулы Крамера.
2. В чем заключается метод Гаусса?
3. Назовите способы вычисления определитель третьего порядка.
Решение систем линейных неравенств. Решение простейших задач линейного программирования
Цель работы: научиться решать системы линейных неравенств, простейшую задачу линейного программирования графическим способом.
Ход работы:
(согласно вариантам)
1. Решить систему линейных неравенств
2. Решить простейшую задачу линейного программирования графическим способом
Пример ВЫПОЛНЕНия заданий
1. Решить систему линейных неравенств
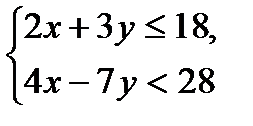
Построим прямые 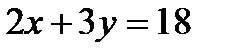 и
и 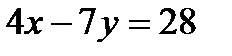 . Первое неравенство нестрогое, поэтому соответствующая ему прямая будет обозначаться сплошной линией. Второе неравенство строгое, соответствующая прямая будет обозначаться пунктирной линией.
. Первое неравенство нестрогое, поэтому соответствующая ему прямая будет обозначаться сплошной линией. Второе неравенство строгое, соответствующая прямая будет обозначаться пунктирной линией.
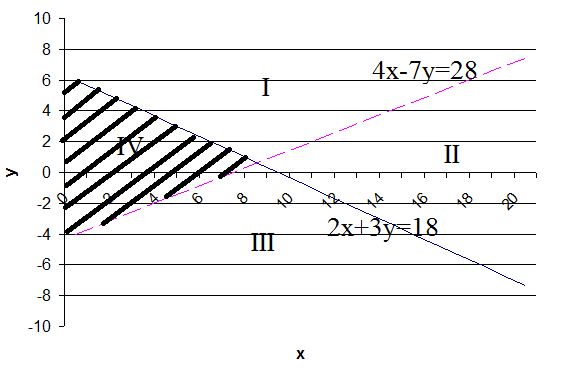
Прямые необходимо подписать.
Проверим точку (0;0). Она удовлетворяет обоим уравнениям системы, следовательно заштриховываем IV часть, в которой лежит точка (0; 0).
2. Для нахождения оптимального решения ЗЛП необходимо:
а) найти область решения системы линейных уравнений с двумя переменными (см.п.1);
б) приравнять целевую функцию к нулю и построить график получившейся прямой;
в) перемещая полученную прямую параллельно вверх (или вниз) найти максимальную (минимальную) точку области решения системы и ее координаты (решить систему уравнений);
г) подставить полученные координаты в целевую функцию.
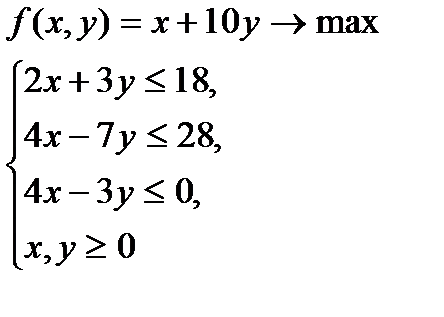
Сначала необходимо найти область решения для системы неравенств (см. задание 1). Область строится в первой четверти координатной плоскости (условия 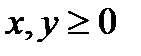 соответствуют первой четверти).
соответствуют первой четверти).
Таким образом, будет получен заштрихованный многоугольник ABCD.

Далее целевую функцию приравниваем к нулю и стоим график получившейся прямой. Перемещаем эту прямую вдоль оси Оу (вверх при  , вниз при
, вниз при  )до тех пор, пока эта прямая не пересечет крайнюю точку многоугольника. В данном примере это будет точка B.
)до тех пор, пока эта прямая не пересечет крайнюю точку многоугольника. В данном примере это будет точка B.
Координаты точки B определим как координаты точки пересечения прямых  и
и 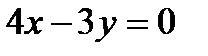 . Для этого нужно решить систему из двух указанных уравнений. Получим B(3;4). Таким образом, максимум целевой функции
. Для этого нужно решить систему из двух указанных уравнений. Получим B(3;4). Таким образом, максимум целевой функции 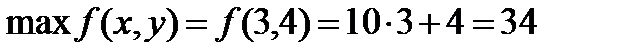 .
.
1 вариант
№1.
 №2.
x+y→max
№2.
x+y→max
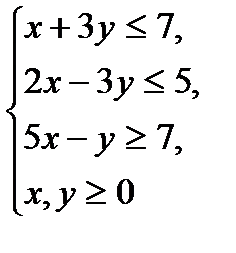
| 4 вариант
№1.
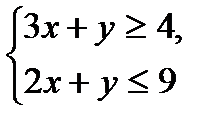 №2.
2x+y→max
№2.
2x+y→max
 
|
2 вариант
№1.
 №2.
3x+y→max
№2.
3x+y→max

| 5 вариант
№1.
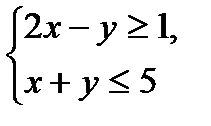 №2.
3x+2y→max
№2.
3x+2y→max

|
3 вариант
№1.
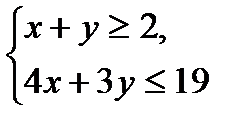 №2.
3x+3y→max
№2.
3x+3y→max

| 6 вариант
№1
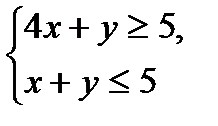 №2.
3x+4y→max
№2.
3x+4y→max

|
7 вариант
№1.
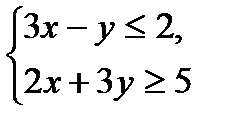 №2.
4x+y→max
№2.
4x+y→max

| 12 вариант
№1.
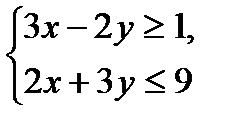 №2.
5x+2y→max
№2.
5x+2y→max
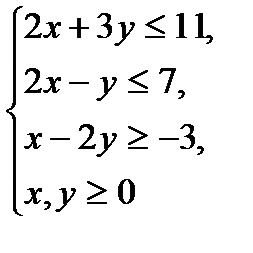
|
8 вариант
№1.
 №2.
4x+2y→max
№2.
4x+2y→max
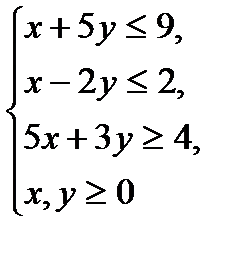
| 13 вариант
№1.
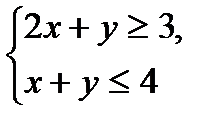 №2.
5x+3y→max
№2.
5x+3y→max
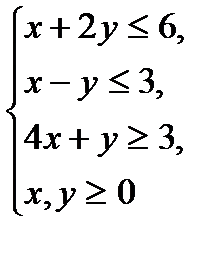
|
9 вариант
№1.
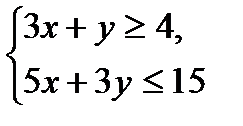 №2.
7x+2y→max
№2.
7x+2y→max
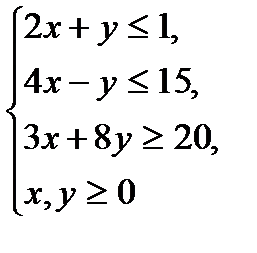
| 14 вариант
№1.
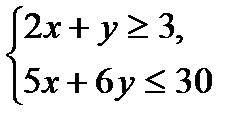 №2.
6x+y→max
№2.
6x+y→max
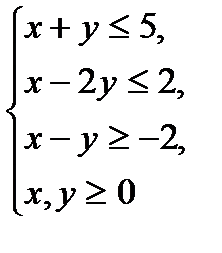
|
10 вариант
№1.
 №2.
4x+3y→max
№2.
4x+3y→max

| 15 вариант
№1.
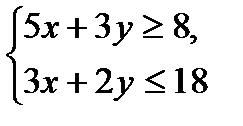 №2.
6x+4y→max
№2.
6x+4y→max
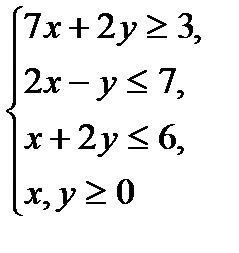
|
11 вариант
№1.
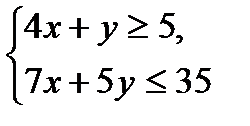 №2.
5x+y→max
№2.
5x+y→max
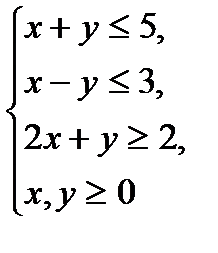
|
Контрольные вопросы:
1. В чем заключается графический способ решения простейшей задачи линейного программирования?
2. Назовите три основные формы задач линейного программирования в зависимости от наличия ограничений разного типа?
- Сколько переменных содержит целевая функция задачи линейного программирования решаемой графическим способом?