С помощью определенного интеграла

Цель работы: научиться вычислять значения геометрических величин с помощью определенного интеграла.

Пример ВЫПОЛНения заданий

1. Найдите площадь фигуры, ограниченной линиями и .

Построим в одной системе координат параболу и прямую . Заштрихуем фигуру, ограниченную этими линиями.

Найдем координаты точек пересечения параболы и прямой как решение системы из двух уравнени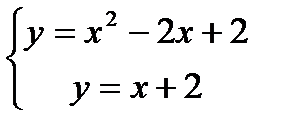й или . Тогда , а .

Далее применим формулу для вычисления площади криволинейной трапеции сверху ограниченной заданной кривой f(x), а снизу осью Ox

Тогда - площадь криволинейной трапеции, ограниченной сверху прямой

- площадь криволинейной трапеции, ограниченной сверху параболой

Тогда площадь S заштрихованной фигуры можно найти

2. Решить задачу на геометрические приложения определенного интеграла

Задача1. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , .

Решение: Сначала в одной системе координат построим параболу и прямую . Выполните самостоятельно.

Найдем их точки пересечения: x₁=0 и x₂=1.

Применим формулу для вычисления объема тела вращения, полученного при вращении вокруг оси Ox фигуры

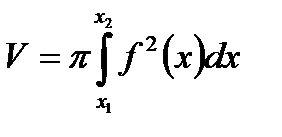
Тогда объем тела вращения, ограниченного прямой

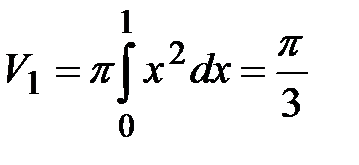
Тогда объем тела вращения, ограниченного параболой

Следовательно искомый объем

Задача2. Найти длину отрезка линии , .

Решение: Воспользуемся формулой для вычисления длины дуги

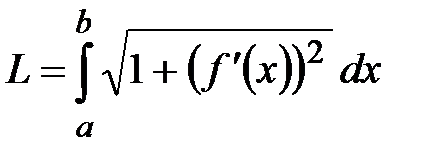
Тогда искомая длина

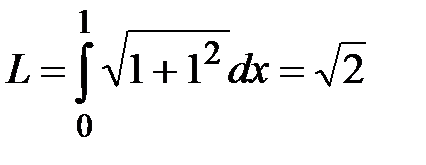
Задача3. Найти длину дуги линии, заданной параметрически .

Решение: Воспользуемся формулой

Тогда искомая длина

Отметим, что во второй и третьей задаче перед вычислением интеграла сначала требовалось найти производные.

Ход работы:

(согласно вариантам)

1. Сделать чертеж к задаче и решить задачу, пользуясь геометрическим смыслом определенного интеграла.

2. Решить задачу на геометрические приложения определенного интеграла.

1 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , .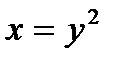

2 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , , .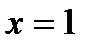

3 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , .

4 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , , ().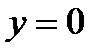

5 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Найти длину дуги линии, заданной параметрически .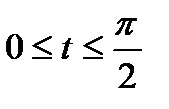

6 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , , , .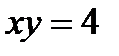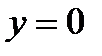

7 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , .

8 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Найти длину дуги линии, заданной параметрически .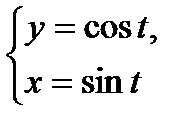

9 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , , .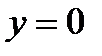

10 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , .

11 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Найти длину дуги линии , .

12 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Найти длину дуги линии, заданной параметрически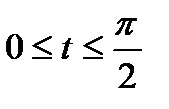

13 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , , , .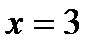

14 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямой . №2. Вычислите объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями , , .

15 вариант №1. Найдите площадь фигуры, ограниченной параболой и прямо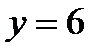й . №2. Найти длину дуги линии , .

Контрольные вопросы:

1. В чем заключается геометрический смысл определенного интеграла?

2. Запишите формулу, по которой вычисляется длина дуги кривой?

3. Запишите формулу, по которой вычисляется объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной заданными линиями?