Цель работы: научиться решать задачи, приводящие к дифференциальным уравнениям.
Ход работы:
(согласно вариантам)
Пример ВЫПОЛНения заданий
Задача 1. На плоскости хОу требуется найти кривую, проходящую через точку О(0; 0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания.
Решение:
Пусть y = f (x) — уравнение искомой кривой. По условию, в каждой точке М(х; f (х)) имеется касательная к этой кривой, угловой коэффициент которой, т. е. f '(x), равен 2х.
Таким образом,  (1) Это дифференциальное уравнение, так как оно содержит производную искомой функции.
(1) Это дифференциальное уравнение, так как оно содержит производную искомой функции.
Из уравнения (1) следует, что функция у есть первообразная функции 2х. Поэтому  или,
или,  (2)где С — произвольная постоянная. Из формулы (2) видно, что дифференциальное уравнение (1) имеет бесконечное множество решений.
(2)где С — произвольная постоянная. Из формулы (2) видно, что дифференциальное уравнение (1) имеет бесконечное множество решений.
Чтобы из этого множества решений выбрать искомое, надо воспользоваться тем, что искомая кривая проходит через точку О (0; 0). Следовательно, координаты этой точки должны удовлетворять уравнению (2), т. е. 0 = 0+С, откуда С = 0.
Итак, искомая кривая — это парабола. 
Задача 2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна нулю.
Решение:
В этом случае, как известно, скорость выражается формулой

Так как скорость прямолинейного движения есть производная пути по времени, то  (3) Из этого уравнения следует, что функция s есть первообразная функции g t. Поэтому
(3) Из этого уравнения следует, что функция s есть первообразная функции g t. Поэтому 
или  (4) Для нахождения произвольной постоянной С воспользуемся тем, что начало отсчета пути совпадает с началом отсчета времени, т. е. s = 0 при t = 0. Подставляя эти значения в равенство (4), имеем 0 = 0 + С, откуда С = 0 и, следовательно,
(4) Для нахождения произвольной постоянной С воспользуемся тем, что начало отсчета пути совпадает с началом отсчета времени, т. е. s = 0 при t = 0. Подставляя эти значения в равенство (4), имеем 0 = 0 + С, откуда С = 0 и, следовательно,
 .
.
| 1 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен половине абсциссы точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 10 м/с2. |
| 2 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;5) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 15 м/с2. |
| 3 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен утроенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 5 м/с2. |
| 4 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(10;0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 12 м/с2. |
| 5 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;3) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 14 м/с2. |
| 6 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 17 м/с2. |
| 7 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(4;4) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 3 м/с2. |
| 8 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;9) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 13 м/с2 |
| 9 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(1;1) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна нулю 16 м/с2. |
| 10 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен квадрату абсциссы точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 18 м/с2. |
| 11 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(4;1) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 6 м/с2. |
| 12 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенному квадрату абсциссы точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 7 м/с2. |
| 13 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(2;2) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 8 м/с2. |
| 14 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(0;1) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 9 м/с2. |
| 15 вариант №1. На плоскости хОу требуется найти кривую, проходящую через точку О(1;0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания. №2. Требуется найти закон движения свободно падающего в пустоте тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна 11 м/с2. |
Контрольные вопросы:
1. Чему равен угловой коэффициент касательной к данной кривой  в данной точке
в данной точке  ?
?
2. Как определить константу С в решении дифференциального уравнения?
3. Что означает фраза «пройденный путь 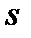 начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна нулю »?
начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна нулю »?