С разделяющимися переменными
Цель работы: научиться решать дифференциальные уравнения с разделяющимися переменными.
Ход работы:
(согласно вариантам)
1. Найти общее решение дифференциального уравнения.
2. Найти частное решение дифференциального уравнения при условии y(1)=1.
Пример ВЫПОЛНения заданий
1. Найти общее решение дифференциального уравнения
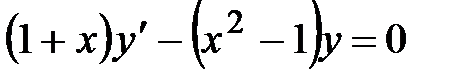
Так как 
, то
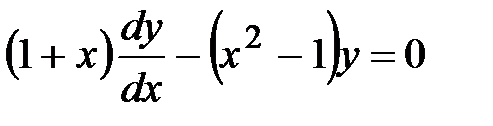
Теперь разделим переменные
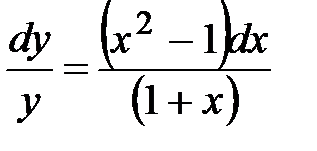
Теперь распишем по формуле
Тогда окончательно уравнение примет вид
Полученное уравнение является уравнением с разделенными переменными, его можно проинтегрировать
- это общее решение исходного дифференциального уравнения
Так как при решении исходного дифференциального уравнения было допущено деление на y, то надо проверить, является ли решением y=0.
Подставляя y=0 в исходное уравнение убеждаемся, что он является частным решением заданного уравнения. Отметим здесь, что y=0, не входит в общее решение, так как натуральный логарифм от нуля не существует.
Ответ. и y=0.
2. Найти частное решение дифференциального уравнения при условии y(2)=1.
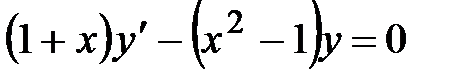
В первом пункте уже было найдено общее решение данного дифференциального уравнения
Теперь воспользуемся данным в условии задачи условием y(2)=1. Подставим в общее решение вместо x число 2, а вместо y число 1.
Откуда получим, что C=0. Тогда искомым частным решением будет
1 вариант
№1. 
№2. 
|
2 вариант
№1.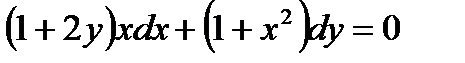 
№2.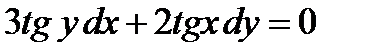 
|
3 вариант
№1. 
№2. 
|
4 вариант
№1. 
№2. 
|
5 вариант
№1. 
№2. 
|
6 вариант
№1 
№2. 
|
7 вариант
№1.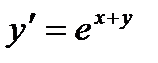 
№2. 
|
8 вариант
№1.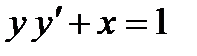 
№2. 
|
9 вариант
№1. 
№2. 
|
10 вариант
№1. 
№2. 
|
11 вариант
№1. 
№2.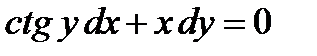 
|
12 вариант
№1. 
№2. 
|
13 вариант
№1. 
№2.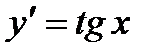 
|
14 вариант
№1. 
№2.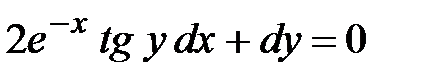 
|
15 вариант
№1.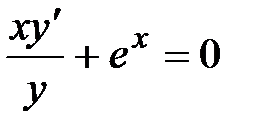 
№2.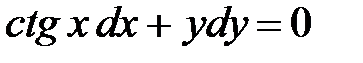 
|
Контрольные вопросы:
1. Дайте определение дифференциального уравнения.
2. Дайте определение порядка дифференциального уравнения.
3. Дайте определения общего и частного решений дифференциального уравнения.
Решение дифференциальных уравнений
Второго порядка
Цель работы: научиться решать дифференциальные уравнения второго порядка.
Ход работы:
(согласно вариантам)
1. Найти общее решение дифференциального уравнения
2. Найти общее решение дифференциального уравнения
3. Найти общее решение дифференциального уравнения
Пример ВЫПОЛНения заданий
1) 
Решение:
Составим характеристическое уравнение:
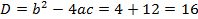
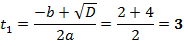
Общий вид решения находится по формуле:
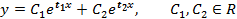
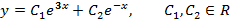
2) 
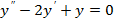
Решение:
Составим характеристическое уравнение:
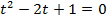
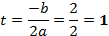
Общий вид решения находится по формуле:
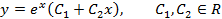
3) 
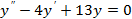
Решение:
Составим характеристическое уравнение:
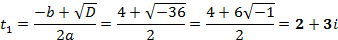
Общий вид решения находится по формуле:
1 вариант
1) 
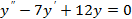2) 
3) 
| 9 вариант
1) 
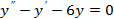2) 
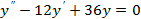3) 
|
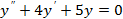
2 вариант
1) 
2) 
3) 
| 10 вариант
1)
2)
3)
|
3 вариант
1) 
2) 
3) 
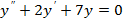
| 11 вариант
1) 
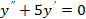2) 
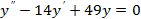3) 
|
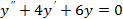
4 вариант
1) 
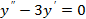2) 
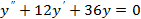3) 
| 12 вариант
1) 
2) 
3) 
|
5 вариант
1) 
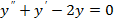2) 
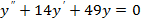3) 
| 13 вариант
1) 
2) 
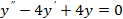3) 
|
6 вариант
1) 
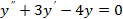2) 
3) 
| 14 вариант
1) 
2) 
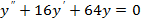3) 
|
7 вариант
1) 
2) 
3) 
| 15 вариант
1) 
2) 
3) 
|
8 вариант
1) 
2) 
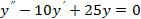3) 
|
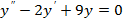
Контрольные вопросы:
1. Дайте определение порядка дифференциального уравнения?
2. Каким образом составляется уравнение характеристик?
3. Сколько условий необходимо задать для нахождения частного решения дифференциального уравнения второго порядка?