Цель работы: научиться решать прикладные задачи с помощью производной.
Пример ВЫПОЛНения заданий
1. Тело движется прямолинейно по заданному закону 
.
a. Найти мгновенную скорость тела в момент времени 
секунду.
b. Найти ускорение тела в момент времени 
секунды.
c. Найти, через сколько секунд от начала отсчета мгновенная скорость тела будет равна 
=44м/с.
d. Найти, через сколько секунд от начала отсчета ускорение тела будет равно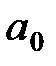 
.
Решение:
a) Для нахождения скорости вычислим производную первого порядка 
. Тогда мгновенная скорость через 1 секунду 
.
b) Для нахождения ускорения вычислим вторую производную 
. Тогда через 2 секунды ускорение будет 
.
c) Для определения времени, по истечении которого скорость тела будет равна 44м/с необходимо решить уравнение 
. Получаем t=2 секунды.
d) Для определения времени, по истечении которого ускорение тела будет равно 22м/с2 необходимо решить уравнение 
. Остается найти t.
Отметим, что если в Вашем варианте в соответствующей колонке стоит прочерк, значит этот пункт делать не надо.
2. Составить уравнение касательной к графику функции 
в точке (1;1).
Решение:
По условию задачи x0=1 и f(x0)=f0=1. Уравнение касательной имеет вид
.
Таким образом, остается найти
Тогда уравнение касательной примет вид
Ход работы:
(согласно вариантам)
1. Тело движется прямолинейно по заданному закону S(t).
a. Найти мгновенную скорость тела в момент времени 
.
b. Найти ускорение тела в момент времени 
.
c. Найти, через сколько секунд от начала отсчета мгновенная скорость тела будет равна .
d. Найти, через сколько секунд от начала отсчета ускорение тела будет равно .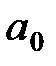
Тело движется прямолинейно по закону S(t)
| № варианта | S(t), (м) | t0 (с) | t1 (с) | v0 (м/с) | a (м/с2) |
| 72 м/с | - | |||
| - | 36 м/с2 | |||
| - | 5,6 м/с2 | |||
| 8 м/с | - | |||
| 21 м/с | - | |||
| 5 м/с | - | |||
| - | 12 м/с2 | |||
| 32 м/с | - | |||
| - | 24 м/с2 | |||
| 20 м/с | - | |||
| - | 10 м/с2 | |||
| 20 м/с | - | |||
| - | 24 м/с2 | |||
| 30 м/с | - | |||
| 10 м/с | - |
2. Составить уравнение касательной к графику функции f(x) в заданной точке.
| № варианта | f(x) | (x0,y0) |
| (-3;-6) | |
| (1;1) | |
| (5;5) | |
| (3;21) | |
| (1;3) | |
| (-3;6) | |
| (1;-3) | |
| (1; 0) | |
| (0;1) | |
| (2;-3) | |
| (1;-3) | |
| (2;-4) | |
| (1;-1) | |
| (1;7) | |
| (0;0) |
Контрольные вопросы:
1. В чем заключается физический смысл производной?
2. Как найти мгновенную скорость в некоторый момент времени 
, если задан закон движения тела?
3. Как найти ускорение тела, если задан закон движения тела?
4. В чем заключается геометрический смысл производной?
Решение прикладных задач на нахождение наибольших и наименьших значений
Реальных величин
Цель работы: научиться решать прикладные задачи на нахождение наибольших и наименьших значений реальных величин.
Ход работы:
(согласно вариантам)
1. Выделить оптимизируемую величину и обозначить ее y.
2. Одну из неизвестных величин положить независимой переменной и обозначить x.Остальные величины выразить через x, пользуясь заданными условиями задачи.
3. Исходя из условий задачи, выразить y через x.
4. Для полученной функции y решить задачу на нахождение наибольшего или наименьшего значения.
5. Интерпретировать результат.
| Вариант №1. Каковы должны быть размеры прямоугольной комнаты, площадью 25м2, чтобы периметр ее был наименьшим? |
| Вариант №2. Требуется огородить сеткой длиной 600м зону отдыха прямоугольной формы, прилегающую к реке. Определите, каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь. |
| Вариант №3. Найдите положительное число, которое, если сложить его с обратным числом даст наименьшую сумму. |
| Вариант №4. Прямоугольный лист жести имеет длину 64 см и ширину 40 см. Из этого листа требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы по прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была максимальной? |
| Вариант №5. Стадион представляет собой прямоугольное поле с областями в виде полукруга, присоединенными к двум его противоположным сторонам. Периметр стадиона должен быть равен 330м. Найдите наибольшую возможную площадь? |
| Вариант №6. Каковы должны быть размеры прямоугольной комнаты, площадью 30м2, чтобы периметр ее был наименьшим? |
| Вариант №7. Требуется огородить сеткой длиной 500м зону отдыха прямоугольной формы, прилегающую к реке. Определите, каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь. |
| Вариант №8. Найдите положительное число, которое, если сложить его с удвоенным кубом обратного числа, даст наименьшую сумму. |
| Вариант №9. Прямоугольный лист жести имеет длину 80 см и ширину 40 см. Из этого листа требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы по прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была максимальной? |
| Вариант №10. Стадион представляет собой прямоугольное поле с областями в виде полукруга, присоединенными к двум его противоположным сторонам. Периметр стадиона должен быть равен 250м. Найдите наибольшую возможную площадь? |
| Вариант №11. Каковы должны быть размеры прямоугольной комнаты, площадью 45м2, чтобы периметр ее был наименьшим? |
| Вариант №12. Требуется огородить сеткой длиной 800м зону отдыха прямоугольной формы, прилегающую к реке. Определите, каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь. |
| Вариант №13. Найдите положительное число, которое, если сложить его с квадратом обратного числа даст наименьшую сумму. |
| Вариант №14. Прямоугольный лист жести имеет длину 40 см и ширину 20 см. Из этого листа требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы по прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была максимальной? |
| Вариант №15. Стадион представляет собой прямоугольное поле с областями в виде полукруга, присоединенными к двум его противоположным сторонам. Периметр стадиона должен быть равен 500м. Найдите наибольшую возможную площадь? |
Пример ВЫПОЛНения заданий
Задача. Каковы должны быть размеры комнаты, чтобы ее площадь была наибольшей, если ее периметр 16.
Решение:
1. Выделим оптимизируемую величину и обозначим ее y – это площадь комнаты, надо найти ее наибольшее значение.
2. Одну из неизвестных величин положить независимой переменной и обозначить x – это одна из сторон комнаты. Остальные величины выразим через x, пользуясь заданными условиями задачи. Вторую сторону комнаты можно выпазить через периметр и x, тогда вторая сторона будет 8-x.
3. Исходя из условий задачи, выразим y через x, так как y – это S прямоугольной комнаты, то y=x(8-x).
4. Для полученной функции y решим задачу на нахождение наибольшего значения. Для этого нужно найти производную функции и приравнять ее к нулю.
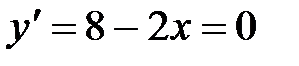
Откуда x=4.
Далее смотри пункт 3 практической работы 6 Исследование функции и построение графика функции с помощью производных.
Самостоятельно начертите рисунок. Таким образом, max y=y(4)=16.
5. Интерпретируем результат.
Комната наибольшей площади имеет форму квадрата со сторонами 4 и 4. Ее наибольшая площадь 16.
Контрольные вопросы:
1. Как найти наибольшее или наименьшее значение функции?
2. Поясните на примере, что значит интерпретировать результат решения задачи?