Понятие о матрицах парных сравнений
После построения иерархии производится сравнение значимости ее элементов. Сравнение этих элементов производится с помощью матриц парных сравнений, которые имеют следующий вид (рис.9.1).
| Сj Ci | C1 | C2 | C3 | C4 | C5 | C6 | C7 | … | CN |
| C1 | а11 | а12 | а13 | а14 | а15 | а16 | а17 | … | а1N |
| C2 | а21 | а22 | а23 | а24 | а25 | … | |||
| C3 | а31 | а32 | а33 | … | |||||
| C4 | а44 | ||||||||
| C5 | а55 | ||||||||
| C6 | а66 | ||||||||
| C7 | а77 | ||||||||
| … | … | … | |||||||
| CN | aN1 | aN2 | aN3 | aN4 | аNN |
Рис.9.1. Матрица парных сравнений
Матрицы парных сравнений строятся следующим образом. Обозначим через  ,
, 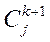 сравниваемую пару элементов, (k =0, 1, 2, …, q), q – общее число уровней иерархии; i – номер элемента, который сравнивается с элементом, имеющим номер j на том же (k+1) уровне иерархии (i,j = 1, 2 … N), N – число элементов на (k+1) уровне иерархии.
сравниваемую пару элементов, (k =0, 1, 2, …, q), q – общее число уровней иерархии; i – номер элемента, который сравнивается с элементом, имеющим номер j на том же (k+1) уровне иерархии (i,j = 1, 2 … N), N – число элементов на (k+1) уровне иерархии.
Обозначим через аij число, соответствующее значимости элемента  по сравнению с
по сравнению с 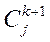 относительно элемента
относительно элемента  , расположенного на вышестоящем k-том уровне иерархии. Элемент
, расположенного на вышестоящем k-том уровне иерархии. Элемент  является в данном случае критерием доминирования элемента
является в данном случае критерием доминирования элемента  над
над 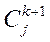 , т.е. какой из двух сравниваемых элементов важнее, предпочтительнее, более вероятен, имеет большее воздействие. Тогда матрицу парных сравнений можно представить так:
, т.е. какой из двух сравниваемых элементов важнее, предпочтительнее, более вероятен, имеет большее воздействие. Тогда матрицу парных сравнений можно представить так:
 , где
, где
(9.1) 
k – номер вышестоящего уровня иерархии;
n – номер элемента  на k-том уровне, относительно которого определены оценки аij элементов
на k-том уровне, относительно которого определены оценки аij элементов  и
и 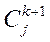 нижестоящего (k+1)-го уровня иерархии;
нижестоящего (k+1)-го уровня иерархии;
i и j – порядковые номера соответственно в строке и столбце матрицы  .
.
Матрица (9.1) обладает свойством обратной симметрии, т.е.  (9.2).
(9.2).
Шкала отношений
Для определения оценок aij будем использовать шкалу отношений, представленную в виде таблицы 9.1. Данная шкала позволяет аналитику ставить в соответствие степеням предпочтения (доминирования) одного сравниваемого элемента иерархии перед другим некоторые числа от 1 до 9.
Шкала отношений (степени значимости действий) Табл.9.1
| Степень значимости | Определение | Объяснение |
| Одинаковая значимость | Два действия вносят одинаковый вклад в достижение цели | |
| Некоторое преобладание значимости одного действия над другим (слабая значимость) | Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны | |
| Существенная или сильная значимость | Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий | |
| Очевидная или очень сильная значимость | Убедительное свидетельство в пользу одного действия перед другим | |
| Абсолютная значимость | Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительно | |
| 3, 4, 6, 8 | Промежуточные значения между соседними суждениями | Ситуация, когда необходимо компромиссное решение |
| Обратные величины приведенных выше ненулевых величин | Если действию i при сравнении с действием j приписывается одно из определенных выше ненулевых чисел, то действию j при сравнении с i приписывается обратное значение | Если согласованность суждений была постулирована при получении N числовых значений для образования матрицы |