Математически, градиент целевой функции Q в точке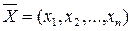 
выражается в виде формулы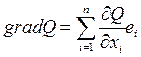 
,
(19.1)
где ei – орты осей переменных xi.
При сложных моделях частные производные в (19.1) не могут быть определены аналитически. Поэтому производится их приближенное вычисление: придавая всем xi поочередно приращения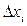 
, вычисляют соответствующие приращения 
.
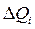1.1. Поиск решения задачи оптимизации градиентным методом
Решение производится следующим образом, графически изображенным на рис.19.1.
Рис. 19.1. Поиск оптимума градиентным методом
В исходной точке А определяется градиент gradQ и делается шаг в направлении градиента. В новой точке В, которая получена после первого шага, снова определяется градиент, делается шаг в его направлении и т.д. до экстремума (максимума или минимума) или до границы области допустимых решений.
1.2. Метод поиска наискорейшего спуска (подъема)
Для ускорения поиска оптимума по градиенту применяется метод наискорейшего спуска (подъема), иллюстрация которого приведена на рис.19.2.
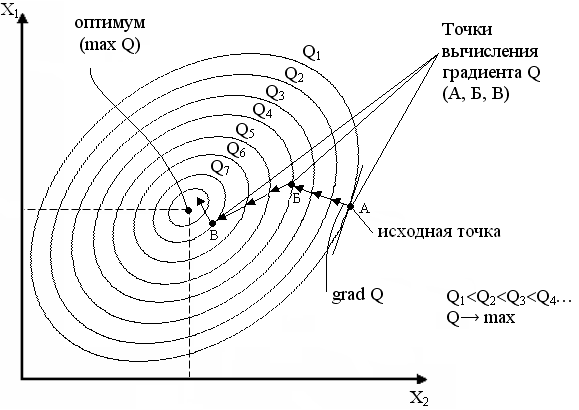
Рис. 19.2. Метод наискорейшего спуска (подъема)
По этому методу в исходной точке А производится вычисление градиента. После этого осуществляется движение по прямой линии, совпадающей с направлением градиента Q. Движение по этой прямой идет до точки Б, в которой прекращается возрастание (убывание) целевой функции Q. В этой точке снова определяется градиент, и движение идет по направлению этого нового градиента и т.д., пока не достигнуты экстремум Q или граница допустимой области.
Поиск по способу «оврагов»
Этот метод применяется в случаях, когда поверхность целевой функции имеет сложную «овражную» форму. Геометрическая иллюстрация этого метода показана на рис. 19.3.
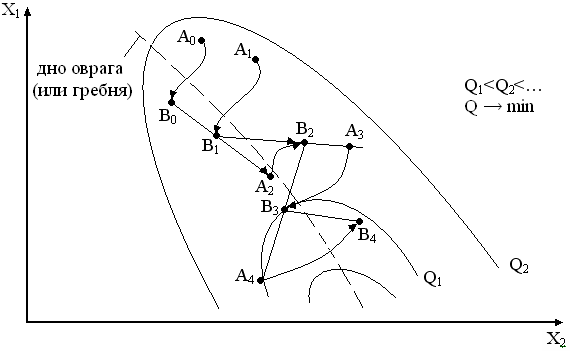
Рис. 19.3. Движение по оврагу
Из исходной точки А0 осуществляется движение по градиенту Q до точки В0, где целевая функция начинает мало меняться (приращение за один шаг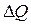 
меньше малой величины e). Затем в стороне от А0 выбирается другая исходная точка А1 и из нее осуществляется движение по градиенту Q до точки В1, где Q начинает мало меняться. После этого делается по прямой В0В1 шаг по «оврагу» до точки А2 и т.д.
Метод зигзагообразного поиска
Этот метод применяется, когда движение по градиенту целевой функции Q натыкается на границу ограничений и возникает проблема дальнейшего поиска экстремума в допустимой области (см. рис. 19.4).
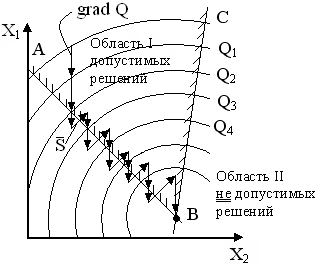
Рис. 19.4. Метод зигзагообразного поиска вдоль границы ограничений
По этому методу после того, как пересекается граница допустимой области, производится возвращение в допустимую область путем движения в направлении вектора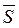 
, представляющего собой сумму градиентов нарушенных ограничений Rj.
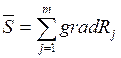
(19.2)
Как только текущая точка поиска снова окажется в допустимой области, движение по 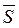сменяется на движение по направлению градиента Q.
Метод функций штрафа
Вместо целевой функции, например,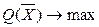 
используется функция 
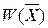, представляющая собой разность функций 
и ограничений 
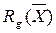, взятых с весовыми коэффициентами 
:
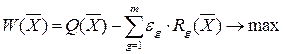
(19.3)
Если выполняются ограничения, то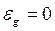 
. В противном случае 
, где Ag – подбираемая для каждого ограничения 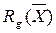константа (вес, значимость ограничения).
В случае, когда ищется максимум в области допустимых решений «штраф не взимается», а при попадании в запрещенную область из «взимается штраф» равный 
. Для поиска экстремума функции 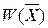могут применяться градиентные и другие методы поиска.
Метод случайного поиска
Этот метод состоит в том, чтобы, осуществляя случайные «бросания точки» в допустимую область, попасть в малую окрестность экстремальной точки. Важнейшие достоинства этого принципа случайного поиска в том, что он не накладывает никаких ограничений на свойства допустимой области и целевой функции.
В частности он пригоден и для поиска глобального экстремума при многоэкстремальных целевых функциях и в случаях, когда область допустимых решений многосвязна. Это можно осуществить с помощью процедуры, представляющей собой комбинацию градиентного метода и метода случайных испытаний (метод Монте-Карло) (см. рис.19.5).
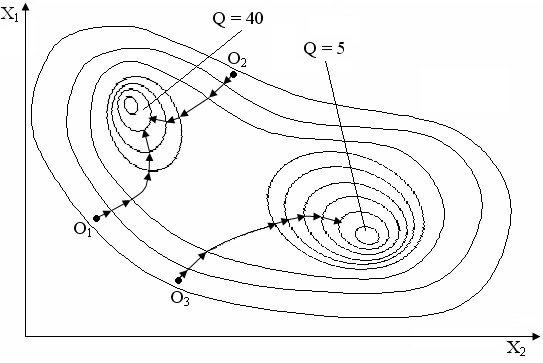
Рис. 19.5. Комбинация градиентного метода и метода случайных испытаний
Методом случайных проб выбираются исходные точки О1, О2, О3. Находится градиентным методом локальные экстремумы. Сравнивая локальные экстремумы, собирают из них глобальный.