Логический анализ систем – это проведение исследований принципов построения систем методами математической логики. В основе такого анализа лежит понятие «формальная система».
2.1. Формальная система
Под формальной (дедуктивной) системой будем понимать совокупность четырех основных множеств (Т, Р, А, В) и двух дополнительных (Г, Д):
Ф = {<Т, Р, А, В> и <Г, Д>},
(11.1)
а также четырех процедур П(Т), П(Р), П(А), П(В).
В этой формуле обозначены:
Т – множество базовых элементов, состоящее из элементов х, которые не могут быть расщеплены на более мелкие элементы. Например, буквы алфавита, слова из некоторого словаря, процессы, функции и т.п. Из базовых элементов будут строиться остальные элементы формальной системы. При этом декларируется, что существует процедура П(Т), которая за конечное число шагов должна дать положительный или отрицательный ответ на вопрос: «Является ли х элементом Т?».
Р – множество синтаксических правил, с помощью которых из элементов множества Т образуются синтаксически правильные совокупности, называемые «правильно построенные формулы» (ППФ). Например, из слов строятся синтаксически правильные фразы, из процессов формируются система менеджмента качества, из операций складывается процесс, из переходов складывается технологическая операция. При этом декларируется существование процедуры П(Р), с помощью которой за конечное число шагов можно получить ответ на вопрос: «Является ли совокупность х синтаксически правильно построенной формулой?».
А – множество аксиом, представляет собой подмножество ППФ произвольно выделенное из множества производных элементов формальной системы. Слово «аксиома» здесь не следует связывать с понятием истинности или ложности ППФ. При этом должна существовать процедура П(А), с помощью которой для любой ППФ можно получить ответ на вопрос о принадлежности ее к множеству А.
В – множество правил вывода, которые служат для того, чтобы с их помощью из множества аксиом можно было получить другие ППФ. Если имеется процедура П(В), с помощью которой можно определить для любой ППФ, является ли она выводимой, то соответствующая формальная система называется разрешимой. Правила вывода имеют общую форму записи
К => Q, где
(11.2)
К – соответствует некоторой совокупности ППФ, которые либо принадлежат А, либо уже были получены из А с помощью правил вывода;
Q – совокупность ППФ, которые выводятся на данном шаге процесса вывода.
<Г,Д> – процедура интерпретации формальной системы, которая определяется двумя множествами;
Г{γ i } – множество значений при интерпретации;
Д{γ i } – множество правил интерпретации, где γ i – значения (смысл), присваиваемые элементам множеств Т, Р, А, В (11.1) и элементам множества К и Q (11.2). Для решения задач логического моделирования в формальной системе применяются методы исчисления высказываний и методы исчисления предикатов.
Физическая интерпретация формальных систем
Когда формальная система используется для описания некоторого объекта реального мира и происходящих в нем процессов, элементы множества Т, Р, А и В приобретают некоторый определенный смысл (из множеств Г и Д), т.е. иначе говоря интерпретируются в рамках того реального объекта или процесса, который формализуется. При этом элементы множества Т приобретают некоторый физический смысл (γ i- значения из множества Г), позволяющий приписывать (с помощью правил множества Д) некоторый смысл и производным элементам, входящим в ППФ.
Пример интерпретации формальной системы
Рассмотрим пример интерпретации формальной системы при описании процесса управления. Систему управления объектом можно представить в виде схемы.
 |
Т – базовое множество информационных сигналов, поступающих от датчиков объекта;
Р – блок синтаксических правил, формирующих совокупности сигналов (по времени, по подобию и др.), необходимых для принятия решения;
А – блок аксиом, отображающих некоторые утверждения о соотношении значений сигналов, верные для всего периода функционирования объекта управления;
В – блок правил вывода для получения производных утверждений о состоянии объекта и выработки управляющих воздействий У.
Лекция 12
Математическое моделирование систем
Классификация моделей
Рассмотрим кратко возможные методы математического моделирования систем. Прежде всего, введем классификацию моделей систем. Чаще всего классификация моделей систем основывается либо на природе связи между элементами в моделируемой системе (вещественные, энергетические и информационные модели), либо на способах моделирования (например, вероятностный или детерминированный, дискретные или непрерывные, с последействием или без последействия). Мы будем использовать классификацию методов моделирования систем в зависимости от усложнения (интеллектуализации) поведения моделируемой системы. Схема такой классификации приведена на рис. 11.1.
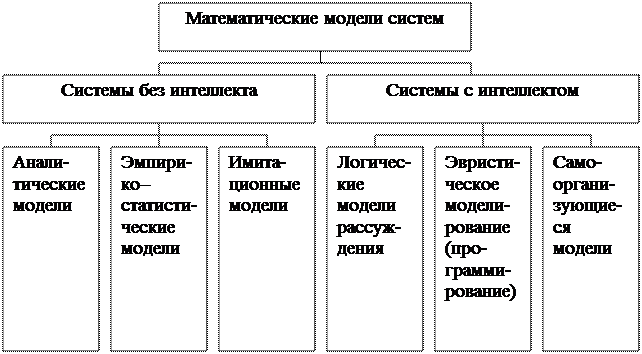
Рис.11.1 Классификация моделей систем
Схема классификации показана на рис. 11.1 является неполной, т.к. охватывает только наиболее распространенные виды моделей. Кроме того, между основными классами нет жесткой границы, они могут частично пересекаться. Рассмотрим основные классы моделей систем.