Геометрическая интерпретация задачи линейного программирования

Рассмотрим следующую задачу:

«Найти значения переменных х₁ и х₂, удовлетворяющих системе ограничений

 

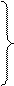
(16.7)

и условиям неотрицательности , для которых целевая функция .»

Для данной двумерной задачи возможна следующая графическая иллюстрация, показанная на рис. 16.1.

Рис. 16.1. Геометрическая иллюстрация задачи линейного программирования

Каждое из неравенств-ограничений (16.7) определяет полуплоскости, пересечение которых дает многоугольник, заштрихованный на рис.16.1. Этот многоугольник и представляет собой допустимое множество решений задач. Зададимся значением целевой функции . График уравнения (пунктирная линия) 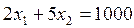представляет собой прямую с отрезками на осях х₁ =500 и х₂ =200. При получим прямую z ₂ параллельную прямой z ₁, но расположенную выше нее. Двигая прямую вверх параллельно самой себе, находим крайнюю точку А, в которой целевая функция z =max. Таким образом, в точке А находим оптимальное решение задачи линейного программирования: .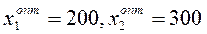

Лекция 17

Симплекс-метод решения задачи линейного программирования

Фундаментальная теорема линейного программирования

Решение 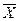называется опорным решением, если оно является угловой точкой области допустимых решений. Геометрическая иллюстрация опорных решений приведена на рис. 17.1.

 

Рис. 17.1. Графическая иллюстрация опорных решений

Теорема (фундаментальная)

Если задача линейного программирования имеет оптимальное решение, то оно совпадает, по крайней мере, с одним из опорных решений системы ограничительных уравнений.

Согласно этой теореме, вместо исследования бесконечного множества допустимых решений с целью нахождения среди них искомого оптимального решения необходимо исследовать лишь конечное число опорных решений. На этом принципиальном положении и основаны методы решения задач линейного программирования.

Принципиальная схема решения задачи линейного программирования

Основываясь на фундаментальной теореме, предложена следующая принципиальная схема поэтапного решения задачи линейного программирования:

Этап 1. Задача приводится к канонической форме (см. предыдущую лекцию).

Этап 2. С помощью симплексных преобразований системы ограничительных уравнений найдем все ее решения.

Этап 3. Вычислим для каждого из опорных решений соответствующие значения целевой функции Z.

Этап 4. Путем сравнения найденных значений Z определим, при каком из опорных решений, функция Z достигает наибольшего значения. Это и будет оптимальным решением задачи линейного программирования.

 

Основы симплекс-метода

В общем случае при больших значениях n (число переменных) количество опорных решений может достигать огромных чисел, и практическое осуществление перебора всех опорных решений станет невозможным. Число анализируемых опорных решений можно резко снизить, если указанный выше перебор опорных решений производить не беспорядочно, а целеустремленно, добиваясь на каждом шаге монотонного изменения функции Z, т.е. чтобы каждое вновь испытываемое опорное решение было «лучше» (соответствовало большему значению функции Z), чем предыдущие. Графическая иллюстрация этого приведена на рис. 17.2. Такая последовательность улучшения решений заложена в основу симплекс метода.

 

Рис. 17.2. Графическая иллюстрация симплекс-метода

 

Альтернативный оптимум

В задачах линейного программирования могут встретиться несколько опорных оптимальных решений (альтернативный оптимум). Графическая иллюстрация альтернативного оптимума показана на рис. 17.3.

 

Рис. 17.3. Графическая иллюстрация альтернативного оптимума

 

В трехмерном случае плоскость целевой функции Z в крайнем положении проходит через грань многогранника допустимых решений. Оптимальное решение задачи – это любая точка указанной грани.

 

Лекция 18