В вычислительной математике существует несколько разных методов вычислений собственных векторов матрицы. В иерархическом анализе систем будем использовать следующие два метода, которые применяются в менеджменте качества.
2.1.Метод последовательных итераций, который мы будем далее называть «точным». В силу трудоемкости он выполняется только на компьютере. По этому методу главный собственный вектор X матрицы 
, соответствующий максимальному собственному значению вычисляется по формуле:
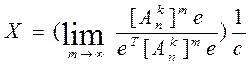, где
(10.2)
m= 1,2,3,… – показатели степени, в которую возводится матрица ;
Т – знак транспонирования вектора (матрицы);
е = {1,1,1,…,1}Т – единичный вектор (транспонирования);
С – константа.
Вычисление собственного вектора Х по формуле (10.2) проводится до достижения заданной точности:
, где
(10.3)
где Xm, Xm-1 – значения собственного вектора, рассчитанные собственно на m-ом и m–1-ом шагах итерации;
- заданная точность итерационного процесса.
Максимальное собственное значение матрицы вычисляется по формуле:
(10.4)
Таким образом, получаем по матрице вектор приоритетов X = (x1, x2, … xN), который в матричной форме представляется так:
2.2.Метод усреднения по нормализованным столбцам,
который далее будем называть «приближенным». Метод позволяет приближенно оценить составляющие вектора Х. При отсутствии компьютера эти простые расчеты могут быть выполнены вручную (на калькуляторе).
Второе правило Саати:
Чтобы получить собственный вектор Х по этому методу, необходимо: разделить элементы каждого столбца на сумму элементов этого столбца, затем сложить элементы каждой полученной строки и разделить эту сумму на число элементов строки.
Это правило можно формализовать и представить в виде следующей формулы для вычисления составляющих 
приближенного вектора приоритетов Х*:
(10.5)
Используя формулу (10.5) можно составить программу и выполнять расчеты на компьютере в случае большего числа матриц парных сравнений при сложной иерархии. В матричной форме полученный приближенный вектор приоритетов представляется так:
Для приближенного определения 
применяется следующее правило. Умножив матрицу справа на полученный по формуле (10.5) приближенный вектора приоритетов, получим новый вектор. Разделив первую компоненту этого вектора на первую компоненту приближенного вектора приоритетов, вторую компоненту на вторую компоненту и т.д., определим еще один вектор. Разделив сумму компонент этого последнего вектора на число компонент N, найдем приближение числу , которое далее используется для оценки согласованности заполнения матрицы .
Это правило можно формализовать и представить в виде следующих формул:
(10.6)
;
(10.7)
;
(10.8)
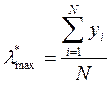, где
(10.9)
– вектор, получающийся после перемножения матрицы на вектор приоритетов;
– матричная форма представления вектора V;
Y = (y1, y2,…, yN) – новый вектор, получающийся после деления компонент;
– приближение к максимальному собственному значению матрицы .