Владелец переводного векселя, выданного на сумму 5 млн. руб. учел его в банке по простой учетной ставке 18% за 42 дня до его погашения.
Определить полученную при учете сумму. Количество дней в году 360.
Ответ: 4,895
Решение: банковский учет:
Финансы и кредит Задача 18
Вексель учтен за год до даты его погашения по учетной ставке 15%.
Какова доходность учетной операции в виде процентной ставки (i)
Ответ: 18%
Решение:
или 18%.
Финансы и кредит Задача 19
Банк выдал кредит в сумме 500 тыс. руб. на три квартала по простой ставке процентов, которая в первом квартале составила 40% годовых, а в каждом последующем увеличилась на 10 процентных пунктов.
Определите погашенную сумму и сумму процентов.
Ответ: 687500 и 187500
Решение:
руб.
сумма процентных процентов:
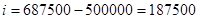руб.
Финансы и кредит Задача 20
Ссуда в размере 1 млн. руб. выдана 20 января до 5 октября включительно под 18 % годовых. Какую сумму должен заплатить должник в конце срока, если начисляются обыкновенные проценты с приближенным числом дней ссуды?
Решение: 1 000 000 · (1 + (255/360) · 0,18) = 1 127 500 руб. = 1,1275 млн. руб.
Ответ: 1,1275 млн. руб.
Деньги
Задача 1
Определить величину денежных агрегатов М0, М1, М2, М3 на основании следующих данных (в млн. ден. ед.):
- наличные денежные средства в банках 500
- срочные вклады населения в Сберегательном банке 1630
- депозитные сертификаты 645
- расчётные, текущие счета юридических лиц 448
- вклады населения до востребования 300
- наличные денежные средства в обращении 170.
Решение:
М0 = наличные денежные средства в обращении;
М1= М0+расчётные и текущие счета юридических лиц+вклады населения до востребования;
М2=М1+срочные вклады населения в сберегательном банке;
М3= М2+депозитные сертификаты и облигации госзайма.
Ответ: М0=170, М1=918, М2=2548, М3=3193 млн. ден. ед.
Задача 2
Дефлятор ВНП составляет 3,6. Номинальный ВНП 4 трлн. руб. Определить реальный ВНП.
Решение:
Ответ: 1,11 трлн. руб.
Пример 1.2.1
Месячный уровень инфляции в течение года равен 3 процентам.
Требуется определить уровень инфляции за год.
Решение. Определим индекс инфляции за год: In = (1 + r) п =
= (1 + 0,03)12 = 1,47; следовательно, уровень инфляции за год r = In –
– 1 = 1,47 – 1 = 0,47 = 47 %.
Ответ. Уровень инфляции за год составляет 47 %.
Пример 1.2.2
Месячный уровень инфляции составляет 10 процентов.
Следует определить индекс инфляции за год и годовой уровень инфляции.
Решение. Индекс инфляции за год равен In = (1 + 0,10)12 = 3,45; уровень инфляции за год равен: r = 3,45 – 1 = 2,45 = 245 %.
Ответ: индекс инфляции за год составляет 3,45; уровень инфляции за год будет равен 245 %.
Пример 1.2.3
Требуется определить индекс инфляции и уровень инфляции за год, если месячный уровень инфляции составляет 6 процентов.
Решение. Проведем необходимые расчеты: In = (1 + 0,06)12 = 2,01; R = 2,01 – 1 = 1,01 = 101 %.
Ответ. Индекс инфляции за год составит 2,01; уровень инфляции за год равен 101 %.
Задача № 14
Каждый месяц цены растут на 2%. Определить, каков ожидаемый индекс инфляции за год.
Решение:
Индекс инфляции (Iигод) = (1+рост цены)n, где n = 12 мес.
Ответ: т.е. цены за год вырастут в 1,27 раза или на 27%
Задача № 15
Уровень инфляции в марте составил 3%, в апреле – 5%, в мае – 3%. Определить индекс инфляции за рассматриваемый период.
Решение: Iигод=(1+αмарт)*(1+αапрель)*(1+αмай)
Ответ: 11,4%
Пример 6.6
16 января 1999 года фактический курс рубля, объявленный Центральным банком РФ по результатам утренней торговой сессии на ММВБ, составил 23 руб. за 1 долл. США. В этот период общий индекс цен внутреннего рынка России и США, рассчитанный специалистами Госкомстата, составлял 0,6.
Требуется рассчитать реальный курс рубля по отношению к доллару США в январе 1999 года.
Решение. Поскольку общий индекс цен внутреннего рынка страны и зарубежного внутреннего рынка составил 0,6, а номинальный курс национальной денежной единицы – 23 руб. за 1 долл. США, расчет реального валютного курса выполним следующим образом:
23 × 0,6 = 13,8 руб. за 1 долл. США.
Ответ. Реальный валютный курс рубля по отношению к доллару США в январе 1999 года составил 13,8 руб. за 1 долл. США.
Пример 6.7
18 ноября 1967 года курс английского фунта стерлингов официально снизился с 2,8 до 2,4 долл. за 1 ф. ст.
Необходимо определить процент девальвации английского фунта стерлингов, учитывая, что он имеет косвенную котировку.
Решение. Если старый курс валюты составлял 2,8 долл. США, новый курс валюты после девальвацииравен2,4 долл. США, то процент девальвации валюты составит: (2,8 – 2,4) / (2,8 × 100) = 14,3 %.
Ответ. Процент девальвации валюты составит 14,3 %.
ЦЕНТРАЛЬНЫЙ БАНК
Пример 2.3.1
Проводя политику «дорогих денег», центральный банк страны решил продать государственные облигации на сумму 10 млрд долл. Известно, что облигации на сумму 1 млрд долл. покупаются населением за счет наличных денег, а остальные – за счет средств, хранящихся в коммерческих банках. Норма обязательных резервов – 20 процентов.
Как изменится в этом случае денежная масса?
Решение. Коммерческие банки приобретают облигации на сумму 10 – 1 = 9 млрд долл. С учетом эффекта мультипликации предложение денег уменьшается на 9 × 1 / 0,2, т.е. на 45 млрд долл.
Если учесть, что уменьшаются и денежные запасы населения, то общий объем денежной массы сократится на 46 млрд долл.
Ответ. Общий объем денежной массы сократится на 46 млрд долл.
Пример 2.3.2
В условиях высокого уровня инфляции (20 процентов годовых) ЦБ старался уменьшить денежную массу в обращении при помощи политики открытого рынка.
Какие меры должен предпринять банк, чтобы снизить инфляцию до 10 процентов годовых при условии, что денежная масса составляла 200 млрд руб., а норма минимальных резервов – 20 процентов?
Решение. Поскольку инфляция должна сократиться вдвое, то, при прочих равных условиях, денежную массу нужно уменьшить в два раза. Следовательно, Центральный банк должен продать государственные ценные бумаги на сумму 100 млрд руб.; с учетом эффекта мультипликатора эта сумма будет в пять раз меньше, т.е. составит 20 млрд руб.
Ответ. ЦБ должен продать государственные ценные бумаги на сумму 20 млрд руб.
Пример 2.4.1
В условиях «перегрева» экономики Центральный банк РФ увеличил учетную ставку с 5 до 10 процентов и предложил к переучету векселя номиналом 100 руб. на сумму 200 тыс. руб.
Как изменится денежная масса в экономике при условии, что норма обязательных резервов составляет 10 процентов?
Решение. Цена векселя снизится с 95 до 90 руб., поэтому коммерческий банк будет заинтересован в приобретении векселей по более низкой цене с тем, чтобы в дальнейшем реализовать их по номиналу. Коммерческие банки, приобретя векселя, изымут необходимую сумму из обращения, т. е. вместо выдачи кредитов предприятиям выкупят векселя у Центрального банка РФ, поэтому с учетом мультипликации денежная масса уменьшится на 200 × 1 / 01 = 2 000 тыс. руб.
Ответ. Денежная масса уменьшится на 2 млн руб.
Пример 2.4.2
Как должна измениться учетная ставка Центрального банка РФ, если в стране наблюдается дефицит денежной массы в размере 500 тыс. руб. при норме обязательных резервов 20 процентов?
Ответ. ЦБдолжен осуществить политику кредитной экспансии, т.е. предложить коммерческим банкам благоприятные условия для переучета коммерческих векселей. Это должно быть осуществлено при помощи уменьшения учетной ставки.
БАНКИ И КРЕДИТ
Пример 2.2.1
Объем денежной массы в стране составил на конец года 202 млрд ден. ед. В начале года центральный банк произвел эмиссию в размере 3 млрд ден. ед. и установил норму обязательных резервов в размере 10 процентов.
Каким будет объем денежной массы в стране?
Решение. Поскольку эмиссия происходит путем кредитования коммерческих банков, вся выпущенная сумма в размере 3 млрд. ден. ед. осела на счетах в коммерческих банках. При условии, что безналичные деньги имеют способность к мультипликативному расширению, общая сумма денежных средств, представленная на денежном рынке коммерческими банками, составит 3 × 1/0,1 = 30 млрд ден. ед.
Таким образом, денежная масса увеличится и составит 202 + 30 =
= 232 млрд ден. ед.
Ответ. Объем денежной массы в стране составит 232 млрд ден. ед.
Пример 2.2.2.
Коммерческий банк имеет депозиты до востребования (В) на сумму 600 млн руб. Сумма выданных кредитов составляет 395 млн руб. Избыточные резервы, которые банк хранит на случай непредвиденных обстоятельств, равны 25 млн руб. Предполагается, что кредиты были выданы на всю сумму депозитов, оставшуюся после отчислений в обязательные резервы, за вычетом избыточных резервов.
Какая норма обязательных резервов действует в банковской системе?
Решение. Общий объем резервов банка составляет 600 – 395 =
= 205 млн руб.
Из них избыточные резервы – 25 млн руб., тогда обязательные резервы (К) составят 205 – 25 = 180 млн руб.
Значит, норма обязательных резервов равна R 0 = К / В = 180 / 600 =
= 0,3, или 30 %.
Ответ. Норма обязательных резервов равна 30 %.
Пример 2.2.3
Суммарные резервы коммерческого банка составляют 220 млн руб. Депозиты равны 950 млн руб. Обязательная норма резервирования депозитов составляет 20 процентов.
Как может измениться предложение денег, если банк решит использовать все свои избыточные резервы для выдачи ссуд?
Решение. При норме резервирования 20 % сумма обязательных резервов составит 950 × 0,2 = 190 млн руб. Следовательно, избыточные резервы равны 220 – 190 = 30 млн. руб.
Если они будут полностью использованы для выдачи ссуд, то дополнительное предложение денег может составить 30 × 1 / 0,2 =
= 150 млн руб.
При расчетах использован депозитный мультипликатор 1 / r, равный 5.
Полученная сумма представляет собой максимально возможное расширение предложения денег в случае, если они не используются за пределами банковской системы.
Ответ. Дополнительное предложение денег составит 150 млн руб.
Пример 2.2.4
Норма обязательных резервов равна 20 процентам. Коммерческий банк хранит еще 5 процентов от суммы депозитов в качестве избыточных резервов, не используя их для активных операций. Величина депозитов составляет 10 млн руб.
Какую максимальную сумму может использовать банк для выдачи ссуд?
Решение. Величина обязательных резервов составит 10 × 0,2 =
= 2 млн руб.
Избыточные резервы равны 10 × 0,05 = 0,5 млн руб.
Тогда суммарные резервы равны 2 + 0,5 = 2,5, или 10 × (0,2 + 0,05) =
= 2,5 млн руб.
Следовательно, храня в виде резервов 2,5 млн. руб. из суммы депозитов, для выдачи ссуд банк может использовать оставшиеся средства 10 – 2,5 = 7,5 млн руб.
Ответ. Банк может использовать для выдачи ссуд 7,5 млн руб.
Пример 2.2.5
Суммарные депозиты банковской системы составляли 100 млрд руб. Избыточные резервы отсутствовали. Центральный банк снизил норму обязательных резервов с 25 до 20 процентов.
Каким может быть максимально возможное расширение денежной массы?
Решение. При исходной норме обязательных резервов их сумма составляла 100 × 0,25 = 25 млрд руб.
Поскольку избыточных резервов не было, оставшиеся средства в сумме 100 – 25 = 75 млрд руб. использовались для активных операций.
После снижения нормы резервирования до 20 % сумма обязательных резервов, которые банки перечисляют в ЦБ, уменьшилась и составила 100 × 0,20 = 20 млрд руб.
Освободившиеся средства в сумме 25 – 20 = 5 млрд руб. банки смогли использовать для выдачи ссуд, запуская процесс кредитной мультипликации.
Максимально возможное расширение денежной массы при этом может составить 5 000 × 1 / 0,2 = 25 млрд руб.
Ответ. Максимально возможное расширение денежной массы составит 25 млрд руб.
Пример 2.2.6
Резервы коммерческих банков составляют 1 млрд долларов. Депозиты равны 4 млрд. долл. Норма обязательных резервов составляет 25 процентов. Если Центральный банк решит снизить обязательную норму резервирования до 20 процентов, то на какую величину может увеличиться предложение денег?
Решение. При существующей норме обязательных резервов (25 %) все резервы банка являются обязательными, поскольку 4 × 0,25 = 1 млрд долл.
После снижения нормы резервирования до 20 % банку можно хранить в качестве резервов уже меньшую сумму: 4 × 0,2 = 0,8 млрд долл.
Высвободившиеся в результате этого средства в сумме 1 – 0,8 =
= 0,2 млрд долл. банк может использовать для выдачи ссуд.
Значит, возможное увеличение предложения денег составит 0,2 × 1 / 0,2 =
= 1 млрд долл.
Ответ. Возможное увеличение предложения денег составит
1 млрд долл.
Пример 3.2.1
ООО «Лика» открывает депозитный вклад в размере 100 млн руб. на срок три месяца с начислением процентов в конце срока действия договора из расчета 60 процентов годовых.
Требуется определить сумму денег, которую клиент получит в банке по окончании срока договора.
Решение. Используем формулу. St = S (1 + inn),
где St – будущая сумма после начисления процентов,
S – настоящая сумма денег,
in – простая процентная ставка (годовая),
n – количество лет.
Подставим данные в формулу: 100 × (1 + 0,60 / 4) = 115 млн руб.
Процент по вкладу составляет 115 – 100 = 15 млн руб.
Ответ. Клиент получит в банке по окончании срока договора 115 млн. руб.
Пример 3.2.2
Банк принимает депозиты на полгода по ставке 10 процентов годовых.
Необходимо определить проценты, выплачиваемые банком на вклад 150 тыс. руб.
Решение. Рассчитаем сумму процентов: I = 150 × 0,1 × 0,5 =
= 7,5 тыс. руб.
Ответ. Проценты, выплаченные банком на вклад 150 тыс. руб., составляют 7 500 руб.
Пример 3.2.3
Депозит в размере 200 тыс. руб. был положен в банк 12 марта и востребован 25 декабря. Ставка процентов составляла 80 процентов годовых.
Требуется определить сумму начисленных процентов при различных методах определения срока начисления и сравнить.
Решение. 1. Вгерманской практике расчетное количество дней хранения депозита равно 20 (количество дней хранения в марте) +
+ 30 (апрель) + 30 (май) + 30 (июнь) +30 (июль) + 30 (август) +
+ 30 (сентябрь) + 30 (октябрь) + 30 (ноябрь) + 25 (количество дней хранения в декабре) – 1 (день приема и день выдачи депозита принимаются за один день) = 284. Расчетное количество дней в году – 360. Тогда сумма начисленных процентов составит I = 284 / 200 000 × 0,8 × 360 =
= 126 222 руб.
2. Во французской практике расчетное количество дней хранения депозита равно 20 + 30 + 31 + 30 + 31 +31 + 30 + 31 + 30 + 25 – 1 =
= 288. Расчетное количество дней – 360.
Окончательно получим I = 200 000 × 0,8 × 288/360 = 128 000 руб.
3. В английской практике расчетное количество дней хранения депозита равно 288, расчетное количество дней в году – 365. Тогда
I = 200 000 × 0,8 × 288/ 365 = 126 247 руб.
Ответ. Для владельца счета более выгодна французская практика начисления процентов, для банка преимущественная практика – германская.
Пример 3.2.4
При открытии сберегательного счета по ставке 120 процентов годовых 20 мая на счет была положена сумма в 100 тыс. руб. Затем 5 июля на счет была положена сумма в 50 тыс. руб., 10 сентября со счета была снята сумма в размере 75 тыс. руб., а 20 ноября счет был закрыт. Требуется определить общую сумму, полученную вкладчиком при закрытии счета.
Решение. Поступление средств на счет составило 100 + 50 – 75 =
= 75 тыс. руб.
При определении процентных чисел будем считать, что каждый месяц состоит из 30 дней, а расчетное количество дней в году равно 360 (германская практика). В этом случае:
– срок хранения суммы в 100 тыс. руб. составил 12 + 30 + 5 – 1 =
= 46 дней;
– срок хранения суммы 150 тыс. руб. составил 27 + 30 + 10 – 1 =
= 66 дней;
– срок хранения суммы 75 тыс. руб. составил 21 + 30 + 20 – 1 =
= 70 дней.
Сумма процентных чисел составит (100 000 × 46 + 150 000 × 66 +
+ 75 000 × 70) / 100 = 197 500.
Постоянный делитель равен 360 / 12 = 3.
Проценты составят 197 500 / 3 = 65 833 руб. Окончательно получим 75 000 + 65 833 = 140 833 руб.
Ответ. Владелец счета при его закрытии получит 140 833 руб.
Пример 3.2.5
За пользование кредитом в 10 000 долл. было уплачено 350 долл.
Кредит погашался по следующему графику:
– 2000 долл. – через 3 месяца;
– 3000 – через 6 месяцев,
– 5000 – через 9 месяцев со дня предоставления кредита.
Определить процентную ставку платы за кредит в расчете на год.
Решение. В этом случае процентное число составит
2 000 × 90 + 3 000 × 180 + 5 000 × 270 = 2 070 000 (валюто-дней или долларо-дней).
Действительно, должник пользовался суммой кредита следующим образом:
– 2 000 долл. в течение 90 дней (3 месяца),
– 3 000 долл. – 180 дней,
– 5 000 долл. – 270 дней.
Среднедневной капитал за год составит:
2 070 000 / 360 = 5 750 долл.
Процентная ставка платы за кредит в расчете на год равна 350 ´
´ 1000 / 5750 = 6,1 %.
Ответ. Процентная ставка платы за кредит в расчете на год равна 6,1 %.
Пример 3.2.6
Требуется определить проценты и сумму накопленного долга, если ссуда равна 50 000 долл., срок ссуды – 3 года, проценты простые, ставка – 22 процента годовых.
Решение. Находим сумму начисленных за весь срок процентов:
I = 50 000 × 30 × 0,22 = 33 000 долл.
Определяем сумму накопленного долга:
S = 50 000 + 33 000= 83 000 долл.
Ответ. Сумма накопленного долга составляет 83 000 долл., проценты – 33 000 долл.
Пример 3.2.7
Через 90 дней согласно договору заемщик должен уплатить 20 000 долл. Кредит выдан под 20 процентов годовых.
Требуется определить первоначальную сумму долга (временная база равна 365 дням).
Решение. По формуле P = S / (1+ in) находим
Р = 20 000 / (1 + 90 × 0,20 / 365 = 19 047,62 долл.
При этом разность (S – Р)является дисконтом Д с суммы, т.е.
Д = 20 000 – 19 047,62 = 953,38 долл.
Ответ. Первоначальная сумма долга составляет 19 047,62 долл.
Пример 3.2.8
Требуется определить, какой величины достигнет долг, равный 20 000 долл. через 3 года при росте по сложной ставке, составляющей 10 процентов годовых?
Решение. Сумма долга составит S = 20 000 × (1 + 0,1)3 = 26 620 долл.
Ответ. Долг достигнет величины 26 620 долл.
Пример 3.2.9
Допустим, что в предыдущем примере проценты начисляются поквартально.
Решение. В этом случае N = 12 = (4 × 3), а наращенная сумма долга составит S = 20 000 × (1 + 0,10 / 4)12 = 27 440 долл.
Ответ. Наращенная сумма долга составит 27 440 долл
Задача № 3
Первоначальная сумма Р = 7000 руб. помещена в банк на срок n = 2 года под процентную ставку i = 15% годовых. Определить будущую сумму, при условии, что начисление процентов осуществляется по схеме простых процентов.
Решение:
FV=P*(1+n*i)
Ответ: 9100 руб.
Задача № 4
Первоначальная сумма Р = 6000 руб., наращенная сумма S = 7200 руб., процентная ставка i = 10% годовых (проценты простые). Определить период начисления процентов (n).
Решение:
Ответ: 2 года
Задача № 5
Наращенная сумма S = 20000 руб., период начисления процентов n = 1,5 года, простая процентная ставка i = 17% годовых. Определить первоначальную сумму (P).
Решение:
Ответ: 15936,25 руб.
Задача № 6
Первоначальная сумма Р = 24000 руб. В первой половине года применялась простая процентная ставка i1 = 12% годовых, во второй половине года применялась простая процентная ставка i2 = 15% годовых. Определить наращенную сумму (S).
Решение:
)
S=P*(1+n1*i1+n2*i2)
Ответ: 27240 руб.
Задача № 7
Кредит на сумму 15000 руб. выдаётся на полгода по простой учётной ставке 12% годовых. Определить, какую сумму получит заёмщик.
Решение:
P=S*(1-n*d)
Ответ: 14100 руб.
Задача № 8
Вексель на сумму 35000 руб. с датой погашения 27 ноября 2010 года был учтён банком 11 августа 2010 года по простой учётной ставке 13% годовых. Продолжительность года составляет 365 дней. Определить, какая сумма была выплачена банком.
Решение:
P=S*(1- 
).
t= 21(август)+30 (сентябрь)+31 (октябрь)+27 (ноябрь) -1=108 дней
Р=35000*(1-0,13*108/365)=33653,70
Ответ: 33653,70 руб.
Задача № 9
Первоначальная сумма Р = 37000 руб. помещена в банк на срок n = 2 года под i = 15% годовых (проценты сложные). Определить наращенную сумму.
Решение:
S=P*(1+i)n
Ответ: 48932,5 руб.
Пример 3.3.1
Банк выдал кредит в размере 5 млн руб. на полгода по простой ставке процентов – 12 процентов годовых. Требуется определить погашаемую сумму и сумму процентов за кредит.
Решение. Погашаемая сумма составляет S = 5 × (1 + 0,5 × 12 / 100) =
= 5,3 млн руб.
Сумма процентов, полученная банком за кредит, равна I = 5,3 –
– 5 = 0,3 млн руб.
Ответ. Погашаемая сумма составляет 5,3 млн руб., проценты за кредит – 0,3 млн руб.
Пример 3.3.2
Банк выдал кредит в сумме 500 тыс. руб. на 3 квартала по простой ставке процентов, которая в первом квартале составила 40 процентов годовых, а в каждом последующем увеличивалась на 10 процентных пунктов. Необходимо определить погашаемую сумму и сумму процентов.
Решение. Определим S = 500 × (1 + 0,25 × 0,4 + 0,25 × 0,5 + 0,25 × 0,6) =
= 687,5 тыс. руб.
Сумма полученных процентов составляет I = 687,5 – 500,0 = 187,5 тыс. руб.
Ответ. Погашаемая сумма составляет 687,5 тыс. руб., сумма процентов – 187,5 тыс. руб.
Пример 3.3.3
Банк выдал долгосрочный кредит в размере 5 млн руб. на 5 лет по годовой ставке сложных процентов, составляющий 80 процентов годовых. Кредит должен быть погашен единовременным платежом с процентами в конце срока. Требуется определить погашаемую сумму и сумму полученных процентов.
Решение. Определим наращенную сумму: S = 5 × (1 + 0,8)5 = 94, 5 млн руб.
Сумма полученных процентов равна I = 94,5 – 5,0 = 89,5 тыс. руб.
Ответ. Погашаемая сумма составит 94,5 млн руб., сумма процентов – 89,5 млн руб.
Пример 3.3.4
Клиент обратился в банк 16 марта для получения ломбардного кредита на стандартных условиях и предоставил в залог 150 единиц ценных бумаг. Величина займа рассчитывается исходя из 80 процентов их курсовой стоимости. Процентная ставка составляет 9 процентов, а затраты банка по обслуживанию долга – 200 руб. На какой кредит может рассчитывать клиент банка, если курс его ценных бумаг составляет 300 руб.?
Решение. Определим курсовую стоимость ценных бумаг: 300 руб. ´
´ 150 ед. = 45 000 руб.
Сумма кредита, которая составляет 80 процентов от 45 000 руб. будет равна 0,8 × 45 000 = 36 000 руб.
Сумма процентов за период с 16 марта по 16 июня (проценты обычные в случае ломбардного кредита, выдаваемого сроком на 3 месяца) составит 36 000 × 0,09 × 92 / 360 = 828 руб.
Затраты составили 200 руб.
Таким образом, заемщик получит 36 000 – 828 – 200 = 34 972 руб.
Ответ. Если курс ценных бумаг составляет 300 руб., а их общее количество – 150 ед., клиент банка может рассчитывать на кредит в сумме 34 972 руб.
Пример 3.3.5
Банк выдал кредит на сумму 1 млн руб. на год. Требуемая реальная доходность операции равна 8 процентов годовых, ожидаемый годовой уровень инфляции принят равным 60 процентов.
Требуется определить ставку процентов по кредиту, погашаемую сумму и сумму полученных процентов.
Решении. Ставка процентов по кредиту составляет: it = 8 + 60 +
+ 8 × 0,6 = 72,8 %.
Погашаемая сумма равна St = 1 × (1 + 0,728) = 1,728 млн руб.
Сумма полученных процентов составляет: I = 1,728 – 1,000 =
= 0,728 млн руб.
Пример 3.3.6
Кредит на сумму 500 тыс. руб. выдан на 200 дней. Расчетный уровень инфляции за год принят равным 80 процентов, реальная доходность операции должна составить 12 процентов годовых, количество дней в году равно 365.
Необходимо определить ставку процентов при выдаче кредита, погашаемую сумму и сумму полученных процентов.
Решение. Для получения реальной доходности в 12 процентов ставка по кредиту должна составить ik = 12 × 80 × 200 / 365 = 97,26 %.
Погашаемая сумма равна S = 500 000 × (1 + 200 / 365 × 0,9726)=
= 766 465,75 руб.
Сумма полученных процентов составляет: I = 76 465,75 – 500 000 =
= 266465,75 руб.
Пример 3.3.7
Кредит на сумму 2 млн руб. выдан на 2 года. Реальная эффективность операции должна составить 8 процентов годовых по сложной ставке процентов, расчетный уровень инфляции 20 процентов в год.
Требуется определить ставку процентов при выдаче кредита, погашаемую сумму и сумму полученных процентов.
Решение. Ставка сложных процентов составит: ik = 8 + 20 + 8 ´
´ 0,2 = 29,6 %.
Погашаемая сумма равна: ST = 2 × (1 + 0,296)2 = 3,36 млн руб.
Сумма полученных процентов равна I = 3,36 – 2,00 = 1,36 млн руб.
Задача № 10
Наращенная сумма S = 41000 руб., период начисления процентов составляет 2 года, сложная процентная ставка = 15% годовых. Определить первоначальную сумму.
Решение:
Р = 
Ответ: 31001,89 руб.
Задача № 11
Первоначальная сумма P = 24000 руб., период начисления процентов составил 5 лет, причём в первые три года применялась сложная процентная ставка равная 12% годовых, а в оставшиеся два года применялась сложная процентная ставка равная 15% годовых. Определить наращенную сумму.
Решение:
S=P*(1+i1)n1*(1+i2)n2
Ответ: 65458,27 руб.
Задача № 12
Первоначальная сумма составляет 14000 руб., период начисления процентов равен двум годам, сложная номинальная процентная ставка составляет 12% годовых. Проценты начисляются ежеквартально. Определить наращенную сумму.
Решение:
Ответ: 17734,78 руб.
Задача № 13
Первоначальная сумма P = 7000 руб., период начисления n = 4 года, сложная учётная ставка составляет 13% годовых. Определить наращенную сумму.
Решение:
Ответ: 12218,59 руб.
Задача № 16
Период начисления (n) составляет 6 месяцев (0,5 года), ожидаемый ежемесячный уровень инфляции 1,5%. Под какую простую ставку ссудных процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность i = 6% годовых (проценты простые).
Решение:
Iигод = (1+ α)n =(1+0,015)6 = 1,0934, т.е. уровень инфляции (α) за рассматриваемый период составил 0,0934, тогда
Ставка ссудных процентов = 
= 
= 0,2524, т.е. 25,24% годовых
Ответ: 25,24% годовых.
Задача № 17
Первоначальная сумма положена в банк на срок январь-июнь под простую ставку ссудных процентов iα=25% годовых. Уровень инфляции в январе составил 0,5%, в феврале – 2%, в марте – 1%, в апреле – 0,5%, в мае – 3%, в июне – 1%. Определить, какова реальная доходность в виде годовой простой ставки ссудных процентов.
Решение:
n = 6 месяцев = 0,5 года.
Iигод =(1+0,005)*(1+0,02)*(1+0,01)*(1+0,005)*(1+0,03)*(1+0,01)=1,0825, т.е. уровень инфляции за рассматриваемый период α =0,0825. Тогда реальная доходность в виде годовой простой ставки ссудных процентов
i = 
Ответ: 7,9% годовых.
Задача №18
Период начисления составляет 2 года, ожидаемый ежегодный уровень инфляции 12%. Определить, под какую ставку ссудных процентов нужно положить первоначальную сумму, чтобы обеспечить реальную доходность i = 6% годовых (проценты сложные).
Решение:
Iи=(1+iα)n =(1+0,12)2=1,2544, т.е. α=0,2544
=(1+0,06)* 
- 1=0,1872
Ответ: 0,1872 или 18,72% годовых.
Задача № 19
Первоначальная сумма внесена на счёт в банке на срок 2 года под сложную ставку ссудных процентов iα = 15% годовых. Уровень инфляции за первый год составил 12%, за второй год – 14%. Определить, какова реальная доходность в виде сложной годовой ставки ссудных процентов.
Решение:
Iи = (1+0,12)*(1+0,14)=1,2768, т.е. уровень инфляции α за рассматриваемый период составил 0,2768. Следовательно, реальная доходность в виде сложной годовой процентной ставки ссудных процентов будет равна:
i= 
= 
- 1=0,0177 или 1,77% годовых.
Ответ: 1,77% годовых.
Задача № 20
Определить, какой вариант инвестирования первоначальной суммы на срок 0,5 года лучше: под простую процентную ставку 18% годовых или под простую учётную ставку 16% годовых.
Решение:
(или 17,4% годовых), т.к. 17,4% ˂18%, то лучше вариант с постой процентной ставкой.
Ответ: лучше вариант с простой процентной ставкой.
Задача № 21
Определить, какой вариант инвестирования первоначальной суммы на срок 2 года лучше: под простую процентную ставку 17% годовых или под сложную процентную ставку 15,5% годовых.
Решение:
i= 
=((1+0,155)2-1)/2= 0,167 или 16,7% годовых, т.к. 16,7%˂17%, то лучше вариант с простой процентной ставкой.
Ответ: лучше вариант с простой процентной ставкой.
Задача № 22
Определить, какой вариант инвестирования первоначальной суммы на срок 2 года лучше: под простую процентную ставку 19% годовых или под номинальную сложную процентную ставку 14% годовых с ежемесячным начислением.
Решение:
=((1+0,14/12)2*12-1)/2=0,1605 или 16,5% годовых, т.к. 16,5%˂19%, то лучше вариант с простой процентной ставкой.
Ответ: лучше вариант с простой процентной ставкой.
Задача № 23
Найти эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке 12% годовых с ежемесячным начислением.
Решение:
12 -1=0,1268 или 12,68% годовых
Ответ: 12,68% годовых
Задача № 24
Найти годовую номинальную сложную процентную ставку (проценты начисляются каждые полгода), эквивалентную сложной процентной ставке 20% годовых.
Решение:
, т.е. 19,09% годовых.
Ответ: 19,09% годовых
Задача № 25
Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Найти будущую сумму ренты постнумерандо.
Решение:
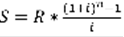= 4127,52 руб.
Ответ: 4127,52 руб.
Задача № 26
Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Найти будущую сумму ренты пренумерандо.
Решение:
= 4705,37 руб.
Ответ: 4705,37 руб.
Задача № 27
Вкладчик в течение 3 лет вносит в банк сумму 1200 руб. Проценты на вклад начисляются по сложной процентной ставке 14% годовых. Определить современную стоимость простой ренты постнумерандо.
Решение:
= 2785,96 руб.
Ответ: 2785,96 руб.
Задача № 28
Определить размер ежегодных платежей в конце года по сложной процентной ставке 14% годовых для накопления через 4 года суммы 70000 руб. (простая рента постнумерандо).
Решение:
=14224,33 руб.
Ответ: 14224,33 руб.
Задача № 29
Определить размер ежегодных платежей в начале года по сложной процентной ставке 14% годовых для накопления через 4 года суммы 70000 руб. (простая рента пренумерандо).
Решение:
=12477,49 руб.
Ответ: 12477,49 руб.
Задача № 30
Взят кредит на сумму 60000 руб. сроком на 4 года под 15% годовых. Определить размер ежегодных погасительных платежей в конце года.
Решение:
= 21015,92 руб.
Ответ: 21015,92 руб.
Задача № 31
Взят кредит на сумму 60000 руб. сроком на 4 года под 15% годовых. Определить размер ежегодных погасительных платежей в начале года.
Решение:
= 18274,71 руб.
Ответ: 18274,71руб.
Задача № 32
Найти наращенную сумму общей ренты сроком (n) 2 года с выплатами (W) по 7000 руб. в конце каждого квартала (p) и начислением процентов по ставке (i) 11% годовых ежемесячно (m).
Решение:
7000* 
Ответ: 61640,85 руб.
Задача № 33
Выдан кредит на сумму 50000 руб. на 3 года по ставке 16% годовых ежеквартально. Определить размер полугодовых платежей.
Решение:
Здесь р = 2, m = 4, i = 
, n = 3*m = 3*4 = 12.
= 
=5327,61* 
=10868,32 руб.
Ответ: 10868,32 руб.
Задача № 34
Найти современную стоимость общей бессрочной ренты с выплатами по 9000 руб. в начале каждого полугодия и процентной ставкой 12% годовых ежеквартально.
Решение:
Здесь р = 2, m = 4, i = 
.
= 
Тогда А= 
Ответ: 147783,33 руб.
Задача № 35
10 августа заёмщик обратился за получением ломбардного кредита и предоставил в залог ценности на сумму 90000 руб. Сумма ломбардного кредита составила 75% от стоимости залога, процентная ставка 14% го