В итоге сводок и группировок статистических данных получают обобщающие показатели, в которых отражаются результаты познания количественной и качественной стороны изучаемого явления. Эти явления можно выразить конкретными статистическими величинами: абсолютными, относительными и средними.
Первичные статистические данные, как правило, представлены абсолютными статистическими показателями, которые выражают размеры (объемы, масштабы, уровни) изучаемых процессов и явлений в следующих единицах измерения:
- натуральных (тонны, штуки, метры, литры и т.п.);
- условно-натуральных (условное топливо с теплотой сгорания 29,3 МДж/кг (7000 ккал/кг), условные консервные банки и т.п.);
- стоимостных (рубли, доллары США, евро и т.п.);
- трудовых (человеко-час, человеко-днях и т.п.).
В отдельных случаях для характеристики какого-либо явления или процесса одной единицы измерения недостаточно, поэтому используется произведение двух единиц. Например, грузооборот и пассажирооборот оцениваются соответственно в тонно-километрах и пассажиро-километрах; производство электроэнергии, измеряемое в киловатт-часах и т.д.
Абсолютные статистические величины представляют собой именованные числа, т.е. имеют какую-либо единицу измерения. Различают два вида абсолютных статистических величин:
- индивидуальные (как результат замера, взвешивания, подсчета и оценки интересующего количественного признака);
- сводные (суммарные, характеризующие объем признака или объем совокупности как в целом по изучаемому объекту, так и по какой-либо его части). К таким показателям относится общая численность занятых в секторе экономике, совокупные активы коммерческих банков региона и т.д.
В процессе выявления ряда важнейших для социально-экономической жизни вопросов возникает необходимость в изучении структуры явления, соотношения между отдельными частями, развития во времени. Поэтому применяются относительные величины, представляющие собой результат деления одного абсолютного показателя на другой, что выражает соотношение между количественными характеристиками социально-экономических процессов и явлений (это производные или вторичные измерители).
Основным условием правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми показателями.
В зависимости от выбора базы сравнения относительный показатель может измеряться в долях единицы с различными единицами измерения:
- разах или коэффициентах (десятых);
- процентах (% - сотых);
- промиллях (о/оо - тысячных);
- продецимиллях (о/ооо - десятитысячных);
- разноименные (руб./чел., ц/га, руб./кв.м и т.п.).
По своему содержанию относительные величины подразделяются на виды: сравнения, характеризующие разные объекты (домашние хозяйства, предприятия, регионы, страны и т.д.); структуры (часть к совокупности в долях единицы или в процентах); динамики (изменение уровня какого-либо явления во времени, текущего периода к предшествующему или к базисному в темпах роста); выполнения программ (программное задание и его фактическая реализация); интенсивности (степень распространения или уровень развития явления в определенной среде, например плотность населения, обеспеченность населения врачами на 10000 человек, число родившихся в среднем за год на 1000 женщин по возрастным группам и т.д.), разновидностью относительных величин интенсивности являются показатели уровня экономического развития (например, уровень ВВП России на душу населения); координации (соотношение отдельных частей целого между собой; например, доля произведенных товаров и услуг в ВВП); эффективности (производительность труда, капиталоотдача и т.д.).
Средней величиной называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
Средняя - это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает. Она отражает типичный, характерный, реальный уровень изучаемых явлений и их изменения во времени и в пространстве.
Однако для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является главным условием научно обоснованного использования средних.
На практике используются различные виды средних чисел. В первую очередь «средние арифметические» величины. Это частное от деления суммы всех результатов измерения на объем измерения. Среднее удобно вычислять после того, как составлена таблица распределения.
Например 3.1, на праздничном вечере среди учеников 11-А и 11-Б классов провели лотерею. Каждый из 50 школьников произвольно задумал одну цифру от 0 до 9 и записал её и на левой и на правой половинках своего лотерейного билета. Правые половинки билетов остались у их владельцев, а левые половинки передали организаторам лотереи. Требовалось определить «самый популярный» ответ и средний? Информацию о результатах лотереи организаторы завели в таблицу, и общая картина распределения полученных данных стала абсолютно ясна:
| Ответ | |||||||||||
| Количество ответов |
Оказалось, что «самым популярным» был ответ 5, который указывался в билетах 10 раз, средний:
0∙2 +1∙5 +2∙3 + 3∙9 + 4∙4 + 5∙10 + 6∙3 +7∙5 + 8∙3 + 9∙5 + 10∙1 = 236:50 = 4,72.
В статистике, как правило, исчисляется система средних показателей:
Средняя арифметическая 
, (3.1)
Средняя гармоническая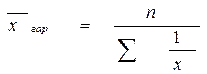 
, (3.2)
Средняя геометрическая 
, (3.3)
Средняя квадратическая 
, (3.4)
Средняя кубическая 
, (3.5)
Существует взаимосвязь средних величин.
Средние величины применяются в форме простой средней и взвешенной средней. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).
Особым видом средних величин являются структурные средние, которые применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Модальным называется интервал с наибольшей частотой. Внутри этого интервала находится значение признака, которому соответствует максимальная плотность распределения. Напомним, что плотность распределения характеризует число единиц совокупности, приходящееся на единицу измерения варьирующего признака.
Мода (Мо) - значение случайной, встречающееся с наибольшей вероятностью, в дискретном вариационном ряду – вариант, имеющий наибольшую частоту. Модой называется такая структурная средняя, у которой возможное значение случайной величины, при котором плотность распределения Р(x) в непрерывном случае, или вероятность Р(X = x) в дискретном случае, достигает максимального значения.
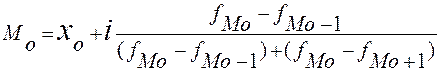, (3.6)
где хо – нижняя граница модального интервал,
i – величина модального интервала,
f мо – частота модального интервала,
f мо - 1 – частота интервала, предшествующего модальному,
f мо + 1 – частота интервала, следующего за модальным.
Например 3.2, на уроке физкультуры 14 школьников прыгали в высоту, а учитель записывал их результаты. Получился такой ряд данных (в сантиметрах):
125, 110, 130, 125, 120, 130, 140, 125, 110, 130, 120, 1125, 120, 125.
Требуется найти размах, моду и медиану измерений?
Решение. Сгруппируем данные в порядке возрастания, разделяя пробелами группы одинаковых результатов:
110,110, 120,120,120, 125,125,125,125,125 130,130,130, 140.
Получился сгруппированный ряд данных. Размах измерения равен 140 – 110 = 30. Вариант 140 встречается однажды, кратность 1. Вариант 110 встречается дважды, кратность равна 2. Вариант 125 встречается наибольшее число раз, её кратность равна 5; это мода измерения. Составим таблицу распределения:
| Варианты | Сумма | |||||
| Кратность |
Если двигаясь по сгруппированному ряду слева направо отсчитать половину (7) результатов, то мы остановимся на результате 125. Следующая половина результатов начинается также со значения 125. Значит 125 – медиана измерения.
Рассчитаем моду для интервального ряда распределения по данным таблицы 3.1.
Таблица 3.1.