1. Цепь переменного тока, содержащая активное сопротивление. При прохождении переменного тока через активное сопротивление, или как иногда говорят, просто через сопротивление (рис. 3.8), около которого не образуется магнитного потока и который не обладает индуктивностью, в любой момент между током и напряжением у клемм этого сопротивления имеет место следующее соотношение:
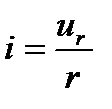или 
.
Если ток изменяется по закону синуса 
, то и напряжение будет меняться по такому же закону
.
Ток и напряжения имеют постоянно одну и ту же фазу, и могут быть представлены двумя совпадающими по направлению векторами (рис. 3.8). Так как амплитуды и действующие значения отличаются лишь множителем 
, то безразлично, что откладывать в векторной диаграмме – амплитуды или действующие значения, они могут быть представлены одним и тем же вектором, но в разных масштабах.
Амплитуда тока равняется амплитуде э.д.с, деленной на сопротивление. В таком же соотношении находятся и действующие значения этих величин:
.
Мощность переменного тока является также величиной, периодически меняющейся. Если в момент t за бесконечно-малый промежуток времени dt через сопротивление проходит dq кулонов электричества и в этот момент напряжение у концов сопротивления равно u, то работа за этот промежуток будет равна 
, а мощность в этот момент, представляющая работу, отнесенную к единице времени, так называемая мгновенная мощность, выразится через
.
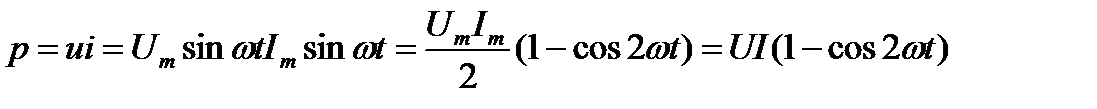Мгновенная мощность, оставаясь все время положительной, меняется в пределах от нуля до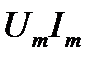 
, совершая в течение одного периода переменного тока два полных цикла (рис. 3.8).
Если говорят про мощность переменного тока, то под этим всегда подразумевают среднюю мощность, которая для любого периода при установившемся режиме есть величина неизменная. Средняя мощность или просто мощность переменного тока, проходящего через омическое сопротивление, равна полу произведению амплитуд.
|
|
Заменяя амплитуды действующими значениями, мы получаем, что
,
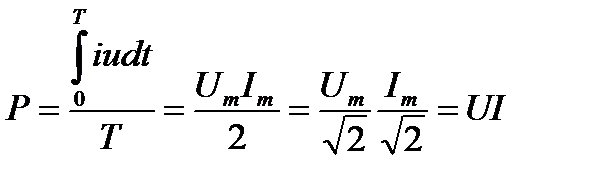т.е. мощность переменного тока, если в цепи имеется одно омическое сопротивление, равна произведению действующих значений напряжения и тока.
Цепь переменного тока, содержащая индуктивность. Когда электрический ток проходит через какой-нибудь проводник или катушку, то вокруг проводника образуется магнитное поле, и поэтому если ток в катушке будет меняться во времени, то меняющийся магнитный поток будет наводить в катушке электродвижущую силу. Явление электромагнитной индукции или индуктивности играет первенствующую роль при прохождении переменного тока через какую-нибудь катушку. С количественной стороны это явление учитывается так называемым коэффициентом индуктивности (самоиндукции) или просто индуктивностью, обозначаемой буквой L.
Индуктивность (или коэффициент индуктивности) L какой-нибудь катушки в абсолютных единицах измеряется как произведение магнитного потока, проходящего через катушку, на число витков w, когда ток в катушке равен единице:
или 
.
Так как магнитный поток при одном и том же токе пропорционален числу витков, то индуктивность катушки пропорциональна квадрату числа витков.
Электродвижущая сила, которая наводится в катушке при изменении тока за время dt на di, будет:
,
.
Причем 
и 
, тогда 
, поэтому один генри можно определить, как индуктивность такой катушки, в которой при равномерном изменении тока на 1А в одну секунду наводится э.д.с., равная 1В.
|
|
Рис. 3.9. Синусоидальный процесс в цепи с L
|
Положим, что нам дана катушка (рис. 3.9), сопротивление которой настолько мало, что им можно пренебречь и положить 
. При прохождении через катушку переменного тока 
в катушке создается переменный по величине и направлению магнитный поток
,
который в любой момент совпадает по фазе с током и который поэтому в линейной диаграмме представляется синусоидой, отличающейся от синусоиды тока только масштабом, а в векторной диаграмме вектором, имеющим то же направление, что и вектор тока.
Изменение тока за время dt на величину di будет сопровождаться наведением в катушке магнитным потоком э.д.с.,
,
которая по фазе отстает от тока на четверть периода или на 
. Поэтому в линейной диаграмме синусоида индуктивной э.д.с., сдвинута вправо на четверть волны, а в векторной диаграмме (рис. 3.9) соответствующий вектор OEL повернут по отношению к вектору тока на 90 
в сторону, обратную движению векторов. Так как индуктивная электродвижущая сила имеет всегда такое направление, что она препятствует всякому изменению тока, то, для того чтобы через индуктивную катушку проходил переменный ток 
, к клеммам индуктивной катушки должно быть приложено напряжение u, которое в любой момент должно быть равно и противоположно и индуктивной электродвижущей силе:
|
|
.
Таким образом, напряжение у клемм представляется синусоидой или вектором, равнопротивоположным(т. е. имеющим значение равное по модулю и противоположное по направлению) синусоиде или вектору индуктивной электродвижущей силы, другими словами, при одной только индуктивности вектор напряжения опережает вектор тока на 90 :
,
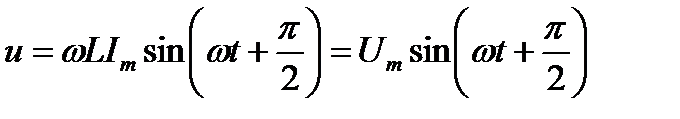и величина этого вектора, представляющего амплитуду напряжения, равна
.
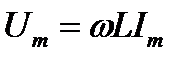Из сказанного вытекает, что если у клемм индуктивной катушки, сопротивление которой равно нулю, действует синусоидальное напряжение
,
то ток будет изменяться также по синусоиде
,
вектор, который будет отставать от вектора напряжения на 90 или четверть периода. Амплитуда тока равна
.
Она прямо пропорциональна амплитуде напряжения и обратно пропорциональна (коэффициенту) индуктивности и числу периодов. В таком же соотношении будут находиться и действующие значения тока и напряжения:
.
Из этого соотношения следует, что величина 
должна измеряться в таких же единицах, как и сопротивление, т.е. в Омах. Величину 
будем называть реактивным сопротивлением индуктивности или реакцией индуктивности и обозначать через х L: 
.
Мгновенная мощность переменного тока в индуктивной катушке
представляется синусоидой с двойным числом периодов, ось симметрии которой совпадает с осью абсцисс (рис. 3.9).
Как видно из рисунка, промежутки времени, в течение которых энергия извне сообщается индуктивной катушке, чередуется с такими промежутками, когда эта энергия возвращается обратно.
В момент, когда ток равен нулю, в катушке не имеется магнитного потока, и нет накопленной энергии. По мере возрастания тока увеличивается потенциальная энергия магнитного поля, которая ввиду отсутствия потерь (r=0) должна равняться работе, получаемой извне. За четверть периода, когда ток от нуля возрастает до своей максимальной величины, эта работа будет равна
.
В следующую четверть периода ток уменьшается от Im до 0, и вместе с этим накопленная энергия будет постепенно возвращаться, пока при i =0 она не будет возвращена полностью. В дальнейшем ток изменит свое направление, и процессы намагничивания с накоплением энергии и размагничивания с отдачей энергии будут чередоваться каждую четверть периода.
Так как в катушке отсутствуют потери, то происходит лишь периодический переход энергии извне к катушке и обратно, и средняя мощность равна нулю:
.
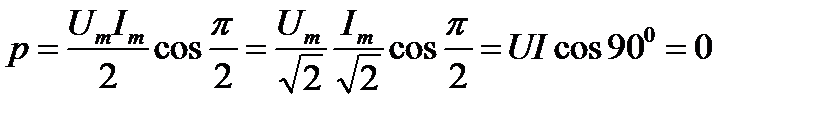Цепь переменного тока, содержащая емкость. Если между двумя изолированными друг от друга проводниками действует какое-нибудь напряжение (или разность потенциалов), то на поверхности проводников появляются равные и противоположные количества электричества, пропорциональные напряжению. Это явление называется явлением емкости, а два проводника, разделенные диэлектриком, - конденсатором.
Емкость измеряется зарядом, соответствующим единице напряжения.
Конденсатор, присоединенный к переменному напряжению 
,мгновенно получает заряд, пропорциональный напряжению, 
(С – емкость конденсатора). Если в проводах, соединяющих конденсатор с источником тока, не происходит падение напряжения, и тогда напряжение у клемм конденсатора постоянно равно и противоположно внешнему напряжению.
В связи с изменением напряжения меняется и количество электричества на обкладках конденсатора. Если напряжение источника тока за промежуток dt возрастает на du, то за этот промежуток времени увеличивается смещение в диэлектрике конденсатора, в результате заряд на обкладках конденсатора увеличивается на
.
Такое же количество электричества должно пройти через провода, а потому ток в проводах (который в диэлектрике переходит в ток смещения) будет равен
.
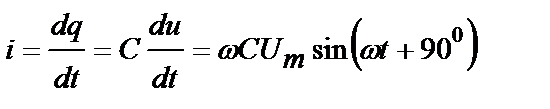При этом мы предполагаем, что сопротивление диэлектрика настолько велико, что так называемая активная проводимость между обкладками равна нулю и мы имеем дело только с токами смещения).
Так как
, то 
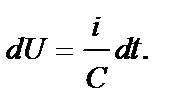
и напряжение у конденсатора в зависимости от тока может представлено следующим образом:
.
На рис. 3.10 представлены значения u и i в зависимости от времени. Когда напряжение увеличивается, 
, ток положителен, перемещение электричества происходит в одном направлении.
Когда достигает своей максимальной величины, 
, заряд прекращается, и ток равен нулю.
При уменьшении напряжения на обкладках конденсаторов получается избыток электричества, конденсатор разряжается, и происходит перемещение электричества в обратном направлении – ток отрицателен. Когда u =0, ток имеет отрицательный максимум. При дальнейшем изменении напряжения, u <0, будет происходить заряд конденсатора в обратном направлении. Синусоида тока опережает синусоиду напряжения на четверть периода, в векторной диаграмме вектор тока OI опережает вектор напряжения OU на 90 .
Рис. 3.10. Синусоидальный процесс в цепи с С
При заданном напряжении 
амплитуда тока
.
Она пропорциональна величине емкости конденсатора и числу периодов. Из последнего соотношения видно, что 
должна измеряться в Омах. Величину 
будем называть реакцией емкости и обозначать через xc. Разделив обе части вышеуказанного соотношения на 
, мы находим зависимость между действующими значениями тока и напряжения:
.
Мгновенная мощность переменного тока в цепи, в которой имеется одна емкость,
представляется также синусоидой с двойной числом периодов, ось симметрии которой совпадает с осью абсцисс. Во время заряда, в промежуток времени четверти периода, в течение которого u меняется от 0 до Um, происходит накопление энергии
.
Эта энергия электростатического заряда освобождается в следующую четверть периода. Заряд и разряд конденсатора в совокупности не требует затраты энергии, и средняя мощность равна нулю:
.
Сравнивая индуктивность и емкость, видим, что при одном и том же напряжении ток в первом случае обратно пропорционален числу периодов и индуктивности, а во втором – прямо пропорционален числу периодов и величине емкости. В случае индуктивности вектор тока отстает от вектора напряжения, в случае емкости опережает вектор напряжения на 90 . В обоих случаях (средняя) мощность равна нулю.