Основные определения в области переменных токов

 

Теория линейных электрических цепей охватывает все многообразие форм изменения тока во времени, встречающихся при использовании электрической энергии. Однако основное внимание уделяется синусоидальному переменному току, т.е. току, являющемуся синусоидальной функцией времени. Это объясняется тем, что в значительном числе случаев практики форма тока мало отличается от синусоиды, и для расчета цепей можно пользоваться методами, разработанными для синусоидальных токов.

Рис. 3.1. Периодическая кривая тока

t

i

T

t1

t3

t2

Кроме того, и это очень важно, во всех случаях передачи сообщений, когда ток явно несинусоидален и представляет собой периодическую или даже непериодическую функцию времени, расчеты линейных электрических цепей могут быть также произведены на основе методов, справедливых при синусоидальных переменных токах. Дело в том, что электрический сигнал в виде напряжения или тока сложной формы может быть разложен на ряд простейших. А одной из простейших форм составляющих сложного сигнала является синусоидальная функция времени. В последующих же главах будет показано, что токи при напряжениях сложной формы могут быть определены как алгебраические суммы токов, создаваемых каждой из синусоидальных составляющих напряжения отдельно.

Таким образом, синусоидальное напряжение должно рассматриваться в качестве основной формы напряжения питания электрических цепей, служащих для передачи сообщений и для передачи и распределения электромагнитной энергии технических частот.

Прежде чем перейти к описанию генератора синусоидального напряжения, введем термины, относящиеся к синусоидальным функциям времени. Определения этих терминов будем связывать с электрическим током в качестве функции времени, хотя эти определения могут быть отнесены и к переменному напряжению или э.д.с.

В том случае, если мгновенные значения тока повторяются через равные промежутки времени, переменный ток называется периодическим переменным током.

Периодом переменного тока называют наименьший промежуток времени, по истечении которого мгновенные значения периодического электрического тока повторяются.

На рис. 3.1 приведена кривая изменения периодического переменного тока. По оси абсцисс отложено время, измеряемое от момента времени, принятого за начало отсчета, а по оси ординат — мгновенные значения тока.

Как следует из определения, для периодического переменного тока всегда справедливо равенство

,

где 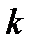— любое целое число; 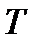— период переменного тока.

В случае периодической кривой тока, изображенной на рис. 3.1, в течение некоторой части периода ток положителен, а в течение другой - отрицателен.

Это означает, что одну часть периода направление тока в двухполюснике совпадает с направлением, принятом нами за положительное направление двухполюснике, а другую часть периода направление тока ему проти­воположно. Площадь, ограниченная огибающей положительных значений тока и осью абсцисс и определяемая как

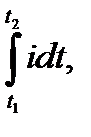
с учетом масштабов тока и времени, в которых строилась кривая, представляет собой заряд, перенесенный в положительном направлении тока за один период. Аналогично, площадь, ограниченная огибающей отрицательных значений тока, представляет собой заряд, перенесенный в обратном направлении за один период.

В узком смысле под периодическим переменным током понимается такой ток, при котором заряд, переносимый током за период, равен нулю. При этом площадь, ограниченная кривой тока и осью абсцисс и вычисленная за период изменения тока, равна

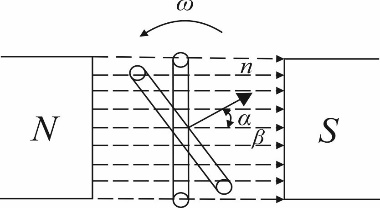
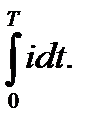
Число периодов тока в одну секунду называется частотой. Таким образом, частота есть величина, обратная периоду

Рис. 3.2. Принцип работы генератора

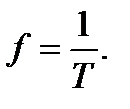
Единица измерения частоты называется герц (1Гц). При частоте в один герц период изменения тока равен одной секунде. Как указано во введении, используемый в современной связи диапазон частот очень широк, поэтому частота часто измеряется в килогерцах (1кГц = 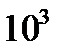Гц), мегагерцах (1МГц = 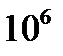Гц) и даже в гигагерцах (1ГГц= Гц).

Условно диапазон частот может быть разделен следующим образом:

1) техническая частота от 50 до 500 Гц,

2) звуковая частота до 10 кГц,

3) высокая частота от 10 кГц и выше.

Верхняя граница радиочастот из года в год отодвигается. В настоящее время верхняя граница может быть принята в 3000 ГГц, Частоты выше 1ГГц обычно называют сверхвысокими частотами.

В качестве генераторов синусоидального напряжения технической частоты чаще всего используются электромашинные генераторы. Источниками звуковых и радиочастот обычно служат ламповые и полупроводниковые генераторы. Принцип и теория работы ламповых и полупроводниковых генераторов излагаются в специальных курсах. Следует отметить только, что любые генераторы могут рассматриваться в качестве генераторов синусоидального напряжения или синусоидального тока.

Принцип работы электромашинного генератора, преобразующего механическую энергию в энергию синусоидального электрического тока, заключается в следующем. Пусть в однородном магнитном поле вращается с постоянной угловой скоростью проволочная рамка (рис. 3.2). Направление магнитных линий на рисунке указано стрелками. Предполагаем, что рамка вращается против направления движения часовой стрелки.

Примем за начало отсчета один из моментов времени, в который нормаль к плоскости рамки совпадает с направлением магнитных линий. При этом магнитный поток, пронизывающий рамку, максимален. Обозначим его Ф _m. В любом другом положении рамки поток, пронизывающий рамку, окажется равным

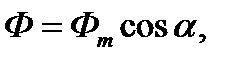
где 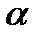— угол между нормалью к плоскости рамки и направлением вектора магнитной индукции 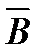(магнитных линий).

Если рамка вращается с постоянной угловой скоростью , то угол поворота рамки может быть записан как функция времени в виде , а поток, пронизывающий рамку,

.

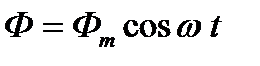При изменении магнитного потока, пронизывающего рамку, в рамке согласно закону электромагнитной индукции индуктируется э.д.с.

,

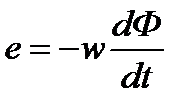где — число витков рамки.

Подставив в последнее равенство выражение магнитного потока, получим

.

Таким образом, э.д.с., возникающая в рамке, изменяется со временем гармонически (по закону синуса), где произведение w – числа витков, ω – угловой частоты и Ф _m – амплитудной величины магнитного потока будет давать амплитудное значение э.д.с., а синусоидальная функция времени – есть гармоническая функция, плавно уменьшающая величину э.д.с., при переходе в противофазу. В течение полуоборота рамки эта э.д.с., имеет одно направление, а в течение другого — обратное. Любое из этих направлений может быть условно принято за положительное. Наибольшее мгновенное значение, равное 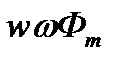, э.д.с., приобретает в момент, когда нормаль к плоскости рамки перпендикулярна линиям магнитной индукции.

Наибольшее значение гармонически изменяющейся величины называется амплитудой. Следовательно, амплитуда э.д.с., возникающей в рамке,

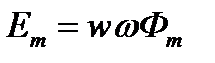. (3.1)

Мгновенное значение э.д.с., записывается в форме уравнения

.

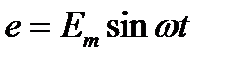В общем случае, если нормаль к плоскости рамки в момент начала отсчета времени составляла с направлением вектора магнитной индукции угол 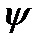, уравнение для мгновенных значений э.д.с., примет вид

. (3.2)

Когда магнитное поле в генераторе создается одной парой полюсов, э.д.с., индуктируемая за один оборот рамки, изменится полностью один раз. В этом случае частота возникающей в рамке э.д.с. равна числу оборотов рамки в секунду, а 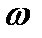— угловой скорости вращения рамки.

Следует заметить, что магнитное поле в генераторе может создаваться не одной парой полюсов, а многими. Более подробно этот материал будет изложен в курсе «Электрические машины».

Необходимость создания генераторов технической частоты с разными числами пар полюсов объясняется тем, что скорости вращения роторов генераторов различны в зависимости от рода первичного двигателя. Если ротор генератора приводится во вращение паровой турбиной, делающей 50 об/сек, то для получения переменной э.д.с., с частотой в 50 Гц необходима одна пара полюсов. Когда же двигателем является тихоходная водяная турбина, для получения той же частоты в 50 Гц необходимо создавать магнитное поле несколькими парами полюсов.

В реальном генераторе рамка-обмотка обычно неподвижна, а вращается система электромагнитов, создающих магнитное поле внутри генератора. Однако эта особенность чисто конструктивного характера и принципиального значения не имеет.

В генераторе с -парами полюсов за один оборот рамки э.д.с., возникающая в ней, изменится полностью раз. Поэтому условимся угловую скорость вращения рамки измерять не в геометрических, а в электрических градусах, приняв за 360 эл. град угол, при повороте на который э.д.с., индуктируемая в рамке, изменится полностью один раз.

Угловая скорость, выражаемая в электрических градусах (или радианах), называется угловой частотой. У генератора с одной парой полюсов значения угловой частоты и угловой скорости одинаковы. У генератора с 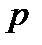-парами полюсов угловая частота в 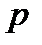раз больше угловой скорости.

Естественно, что если при повороте ротора на 360 эл. град или на 2 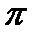рад., э.д.с., претерпевает полное изменение, то продолжительность этого поворота и является периодом изменения э.д.с.

Отсюда ясно, что угловая частота

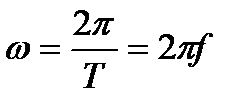(3.3)

равна частоте, умноженной на 2 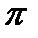, независимо от конструкции и типа генератора.

Если в выражении (3.2) считать 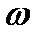угловой частотой, то при иссле­довании электрической цепи, находящейся под воздействием перио­дически изменяющейся э.д.с., выяснение числа пар полюсов генератора, числа оборотов его ротора в секунду и вообще принципа работы генератора не является существенным. Фазой называют значение аргумента гармонической функции, если эта функция выражена в виде синуса*. 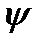Таким образом, аргумент есть фаза э.д.с., Угол , отсчитываемый в градусах или радианах, называется начальной фазой. Он представляет собой значение фазы синусоидально изменяющейся э.д.с. в момент начала отсчета времени.

На рис. 3.3 изображены кривые изменения потока, пронизывающего рамку и э.д.с., индуктируемой в рамке. Если по оси абсцисс откладывать время наблюдения t, отсчитываемое от произвольно выбранного начала отсчета времени, то отрезок, равный расстоянию между двумя точками кривой с одинаковыми фазами, в масштабе времени будет равен периоду Т. Если же по оси абсцисс откладывать произведение 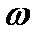t, то тот же отрезок окажется равным 360°, или 2 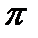рад.

Выбор начала отсчета времени и положительных направлений магнитного потока и э.д.с., произволен.

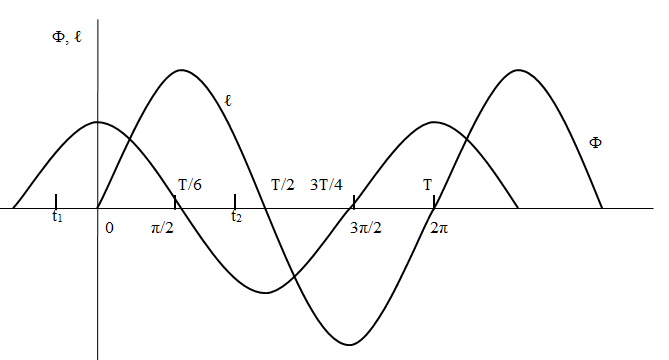Рис. 3.3. Кривые мгновенных значений e и Ф

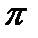На рис. 3.3 начальная фаза магнитного потока равна /2, а

начальная фаза э.д.с. равна нулю. Уравнение магнитного потока и э.д.с. в этом случае должны быть записаны в следующем виде:

,

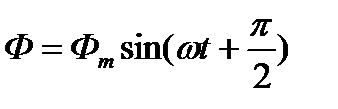Если за начало отсчета времени выбрать момент, отмеченный на рис. 3.3 точкой t₁, то предыдущие уравнения примут несколько другой вид:

,

,

где 0 < < .

Если за начало отсчета времени принять момент t₂, то начальная - фаза потока окажется отрицательной:

,

,

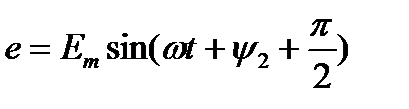где - 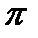< < 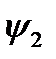0.

Из уравнений и соответствующих им кривых видно, что магнитный поток и индуктируемая им э.д.с. изменяются с одинаковой частотой, но при этом магнитный поток опережает по фазе э.д.с. на 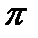/2 или по времени на четверть периода T/4.

Следует отметить, что изображение генератора на схеме не обязательно. В качестве условного источника питания можно пользоваться изображением двух зажимов генератора, находящегося за пределами рисунка. Если в качестве генератора предполагается генератор напряжения, то подключенная к зажимам цепь находится под напряжением

.

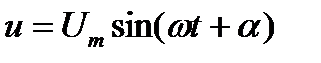Если в качестве генератора предполагается генератор тока, то ток в цепи, подключенной к этим зажимам, будет изменяться согласно уравнению

.

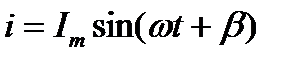Начальные фазы напряжения или тока зависят от выбора начала отсчета времени. Если этот выбор не имеет принципиального значения, то начальную фазу 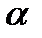или 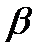можно считать равной нулю.