Изображение мгновенных значений синусоидальных функций времени с помощью кривых дает наглядное представление об амплитудах синусоид, их начальных фазах и разностях фаз между ними. Однако при расчетах электрических цепей необходимо производить простые математические операции над этими функциями.
Можно убедиться в том, что даже сложение двух синусоидальных функций графическим путем с помощью изображающих их синусоид или аналитическим путем с помощью уравнений этих кривых, операция достаточно громоздкая. Например, требуется определить суммарную э.д.с., двух генераторов, включенных последовательно. Напряжения генераторов заданы уравнениями:
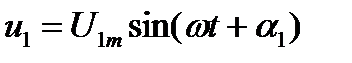 ,
,
 .
.
Задача сложения двух синусоидальных функций заключается в определении формы результирующей функции, ее максимального значения и начальной фазы. Суммарное напряжение обоих генераторов

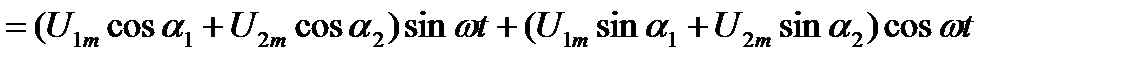 .
.
Обозначая коэффициент при sin  t через А и коэффициент при cos
t через А и коэффициент при cos  t через В, получим
t через В, получим
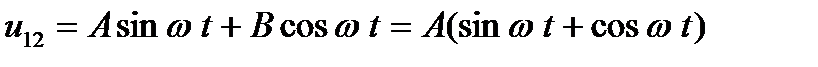 .
.
Отношение  заменим тангенсом некоторого угла
заменим тангенсом некоторого угла  :
:  = tg
= tg 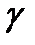 . Тогда
. Тогда

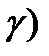 .
.
Таким образом, сумма двух синусоидальных функций одинаковой частоты есть синусоидальная функция той же частоты. Начальная фаза этой синусоиды

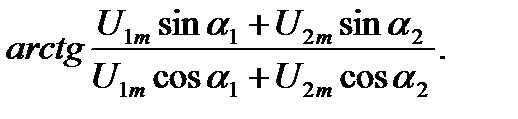
Амплитуда же полученной синусоиды

Расчет упростится и операция сложения получит большую наглядность, если воспользоваться изображением синусоидальных функций с помощью векторов, т. е. так называемой векторной диаграммой.
 Рис. 3.4. Построение синусоиды по вращающемуся вектору
Рис. 3.4. Построение синусоиды по вращающемуся вектору
|
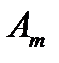 синусоидальной функции. Пусть этот вектор вращается с угловой скоростью
синусоидальной функции. Пусть этот вектор вращается с угловой скоростью 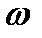 против движения часовой стрелки вокруг начала координат (рис. 3.4). Предполагаем, что в момент начала отсчета вектор был расположен под углом
против движения часовой стрелки вокруг начала координат (рис. 3.4). Предполагаем, что в момент начала отсчета вектор был расположен под углом 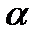 к горизонтальной оси.
к горизонтальной оси.
Тогда при вращении вектора его проекция на вертикальную ось будет изменяться по закону синуса, а мгновенное значение проекции в выбранном масштабе 
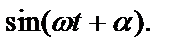
В дальнейшем вместо того, чтобы иллюстрировать работу той или иной электрической цепи с помощью синусоид токов, напряжений и э.д.с., т. е. с помощью так называемой временной диаграммы, можно строить векторы, равные амплитудам этих токов, напряжений и э.д.с., и располагать их таким образом, чтобы проекции векторов на вертикальную ось были равны мгновенным значениям отображаемых ими синусоидальных величин в момент начала отсчета. На рис. 3.4 представлен график синусоидальной функции (временная диаграмма) и вектор, отображающий эту функцию, равный ее амплитуде. Вектор направлен так, что проекция его на вертикальную ось равна мгновенному значению функции в момент начала отсчета времени.
 Рис. 3.5. Векторные диаграммы
Рис. 3.5. Векторные диаграммы
|
 и
и 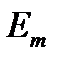 будет соответствовать векторной диаграмме рис. 3.5,б.
будет соответствовать векторной диаграмме рис. 3.5,б.
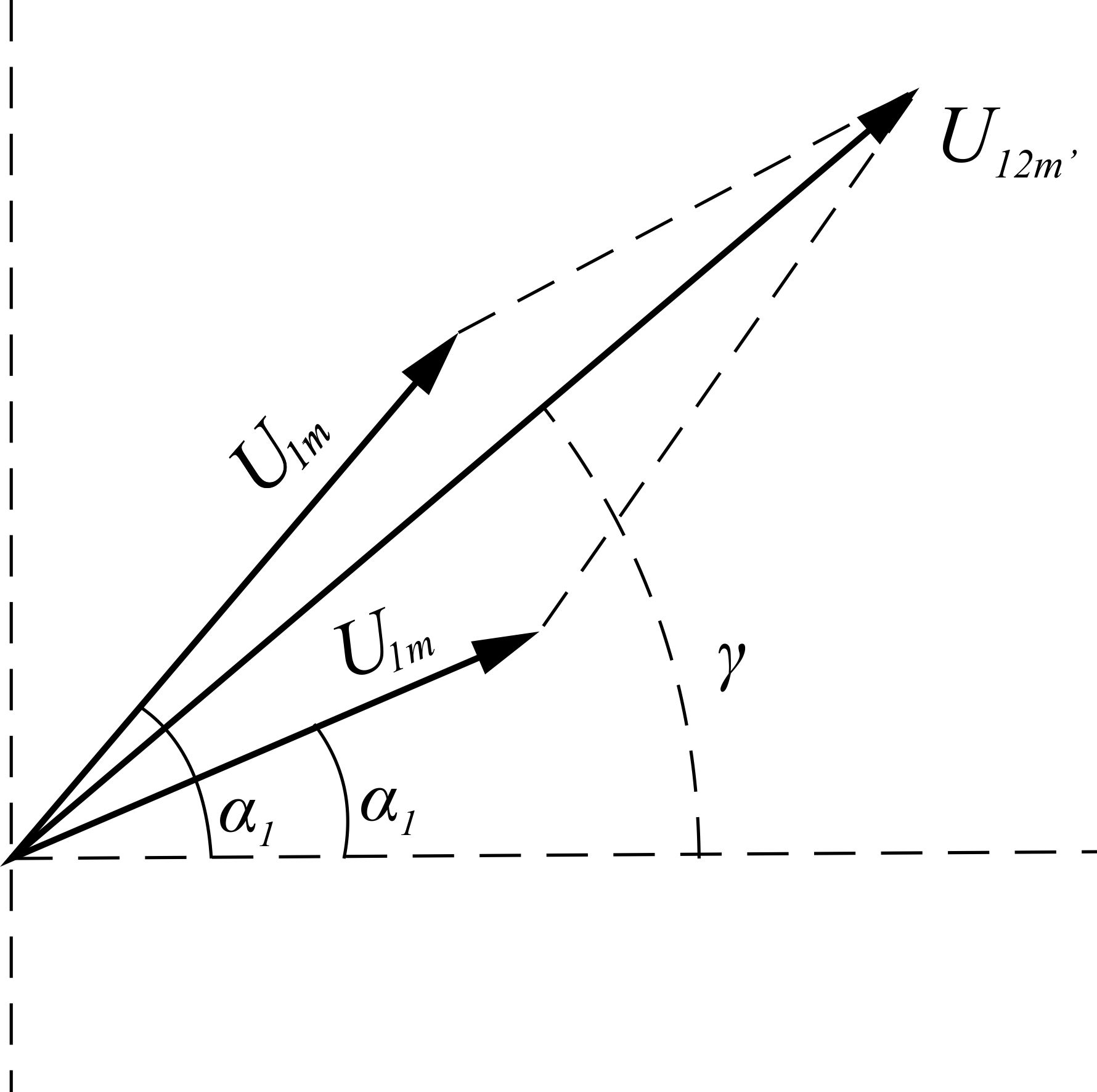 Рис. 3.6. Сложение векторов
Рис. 3.6. Сложение векторов
|
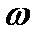 . Если момент наблюдения вращающихся векторов принять за начало отсчета, то углы, составляемые векторами с осью абсцисс, будут представлять начальные фазы отображаемых синусоидальных функций времени.
. Если момент наблюдения вращающихся векторов принять за начало отсчета, то углы, составляемые векторами с осью абсцисс, будут представлять начальные фазы отображаемых синусоидальных функций времени.
Начальные фазы могут быть положительными и отрицательными. Для определения мгновенного значения синусоидальной функции в тот или иной момент времени достаточно найти проекцию соответствующим образом расположенного в этот момент времени вектора на вертикальную ось. Кстати говоря, проекция вектора на горизонтальную ось при вращении вектора будет также изменяться по синусоидальному закону:


 .
. 
Следует отметить, что изображенные с помощью векторов токи и напряжения не являются векторными величинами в обычном смысле слова. Это не пространственные векторы, направление которых указывает на направление действия данной физической величины (например, силы, напряженности поля и т. п.), а условные вращающиеся векторы, направление которых в тот или иной момент времени указывает значение фазы отображаемой синусоидальной функции в момент ее наблюдения.
С помощью векторной диаграммы рассмотренная ранее задача о величине и начальной фазе суммарного напряжения двух генераторов, включаемых последовательно, решается очень просто. Действительно, изобразим с помощью двух векторов амплитуды напряжений обоих генераторов (рис. 3.6), предположив  . Суммарное напряжение, как уже доказано, будет также изменяться по синусоиде, причем ее мгновенные значения должны равняться алгебраической сумме мгновенных значений напряжений обоих генераторов. Так как мгновенные значения определяются проекциями вращающихся векторов на неподвижную ось, а проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на ту же ось, то, сложив геометрически вектор
. Суммарное напряжение, как уже доказано, будет также изменяться по синусоиде, причем ее мгновенные значения должны равняться алгебраической сумме мгновенных значений напряжений обоих генераторов. Так как мгновенные значения определяются проекциями вращающихся векторов на неподвижную ось, а проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на ту же ось, то, сложив геометрически вектор  с вектором
с вектором  , получим новый вектор
, получим новый вектор  , изображающий амплитуду суммарного напряжения. Проекции вектора
, изображающий амплитуду суммарного напряжения. Проекции вектора 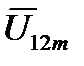 на ту же неподвижную ось равны мгновенным значениям суммарного напряжения обоих генераторов.
на ту же неподвижную ось равны мгновенным значениям суммарного напряжения обоих генераторов.
Рассматривая треугольник, составленный из амплитуд  ,
, 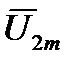 и
и  , можно определить выражение амплитуды
, можно определить выражение амплитуды 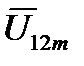 , полученное ранее более сложным путем. Начальная фаза
, полученное ранее более сложным путем. Начальная фаза  может быть также определена из рисунка. Таким образом, сложение двух (или нескольких) синусоидальных функций (токов, э.д.с., напряжений и т.п.) может быть осуществлено путем геометрического сложения отображающих их векторов. Вектор, равный геометрической сумме отображающих векторов, будет отображать суммарную синусоидальную функцию. Его проекция на выбранную неподвижную ось будет представлять собой синусоидальную функцию, равную алгебраической сумме складываемых синусоидальных функций.
может быть также определена из рисунка. Таким образом, сложение двух (или нескольких) синусоидальных функций (токов, э.д.с., напряжений и т.п.) может быть осуществлено путем геометрического сложения отображающих их векторов. Вектор, равный геометрической сумме отображающих векторов, будет отображать суммарную синусоидальную функцию. Его проекция на выбранную неподвижную ось будет представлять собой синусоидальную функцию, равную алгебраической сумме складываемых синусоидальных функций.