Параллельное соединение пассивных двухполюсников

 

Рис. 3.20. Синусоидальный процесс в цепи r, L, C (параллельное соединение)

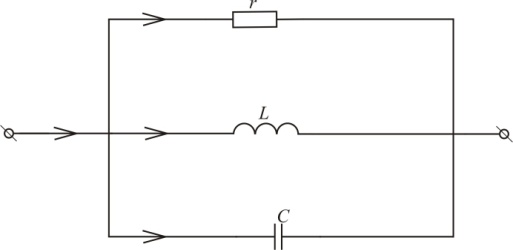Рассмотрим электрическую цепь, содержащую индуктивность, емкость и активное сопротивление в параллельном соединении (рис. 3.20). Если напряжение, приложенное к цепи, u=U_msinωt, то ток в активном сопротивлении

в индуктивности

и в емкости

.

Построение векторной диаграммы для цепи начинаем с вектора, изображающего приложенное к цепи напряжение. Так как это напряжение задано с начальной фазой, равной нулю, изображающий его вектор удобно расположить горизонтально (рис. 3.21). При построении диаграммы пользуемся действующими значениями токов и напряжений. Вектор тока в активном сопротивлении совпадает по направлению с вектором напряжения. Вектор тока в индуктивности отстает от вектора напряжения на π/2, а вектор тока в емкости опережает напряжение на емкости на π/2. Мгновенное значение неразветвленного тока может быть найдено с помощью первого закона Кирхгофа. При выбранных положительных направлениях токов

.

При построении векторной диаграммы вектор тока в индуктивности I_L и вектор тока в емкости I_C строим из конца вектора тока через активное сопротивление I_а. Геометрическая сумма этих трех векторов обозначена буквой I без индекса. Согласно векторной диаграмме

.

Рис. 3.21. Векторная диаграмма для цепи (рис.3.20)

Такое простое соотношение получено потому, что токи в ветвях цепи оказались сдвинутыми между собой на угол, равный π/2 или π.

Прямоугольный треугольник, составленный из векторов токов в ветвях и общего тока, называется треугольником токов. Составляющая вектора общего тока, совпадающая по направлению с вектором напряжения, называется активной составляющей тока или активным током I_а. Составляющая вектора общего тока, перпендикулярная к вектору напряжения и равная 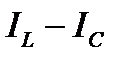, называется реактивной составляющей тока или реактивным током:

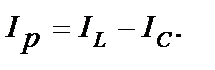
Полной проводимостью цепи называют величину, равную отно­шению общего тока в цепи к напряжению на ее зажимах:

Активной проводимостью цепи называют отношение средней мощности, расходуемой в цепи, к квадрату действующего значения напряжения, приложенного к цепи: =P/U₂.

Последнее выражение можно привести к виду

.

Рис. 3.22. Треугольник проводимостей.

Следовательно, активная проводимость цепи может быть определена как отношение активной составляющей тока на входе цепи к напряжению на ее зажимах. Величина, равная отношению реактивной составляющей тока на входе цепи к значению напряжения на ее зажимах, называется реактивной проводимостью цепи:

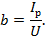
Разделив все стороны треугольника токов на общее напряжение, получим треугольник проводимостей, катетами которого будут b и g и гипотенузой у (рис. 3.22). Определим проводимости каждой из ветвей цепи. В первой ветви ток совпадает по фазе с напряжением.

Следовательно, первая ветвь не содержит реактивной составляющей тока и ее реактивная проводимость равна нулю:

.

Активная проводимость первой ветви

Во второй и третьей ветвях ток и напряжение сдвинуты между собой на угол в 90°, поэтому в них активные составляющие токов и активные проводимости их ветвей равны нулю:

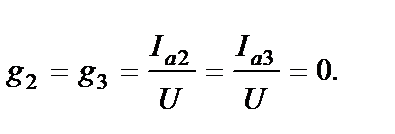
Проводимость второй ветви, содержащей только индуктивность, представляют собой, индуктивную проводимость:

а проводимость ветви, содержащей только емкость, — емкостную проводимость

Подобно тому как в цепи, содержащей L и С в последовательном соединении, под реактивным сопротивлением цепи понималось сопротивление х = х_l-х_C, в цепи с параллельным включением L и С под реактивной проводимостью цепи b понимается разность между проводимостью ветви с индуктивностью и проводимостью ветви с емкостью:

При построении рис. 3.21 и 3.22 предположили b_L>b_C, т. е. что реакция цепи индуктивная. Общий ток в цепи отстает по фазе от приложенного к цепи напряжения. При этом реактивная проводимость b положительна. Из треугольника проводимостей находим

, ,

, . (3.12)

Таким образом, реактивная проводимость цепи может быть величиной и положительной и отрицательной.

Если приемник содержит только индуктивность, то b> 0 и φ> 0, и если только емкость, то b< 0 и φ<0.

Несмотря на то, что проводимости g, b и у не являются векторами, они изображены на диаграмме со стрелками, указывающими направление соответствующих составляющих вектора тока в этих проводимостях.

Если цепь состоит из ряда параллельно включенных активных и реактивных сопротивлений, то для нахождения общего тока нужно геометрически сложить все токи в ветвях. Так как токи во всех активных сопротивлениях совпадают по фазе с напряжением на зажимах цепи, а в реактивных сопротивлениях в зависимости от характера сопротивления сдвинуты по фазе на угол ±π/2 относительно того же напряжения, общий ток в цепи может быть найден как гипотенуза прямоугольного треугольника токов.

Одним из катетов этого треугольника, или активной составляющей общего тока, будет арифметическая сумма всех активных токов в ветвях ΣI_а, а другим катетом, или реактивной составляющей общего тока, — алгебраическая сумма всех реактивных токов в ветвях ΣI _p: