Рис. 3.37. Изображение
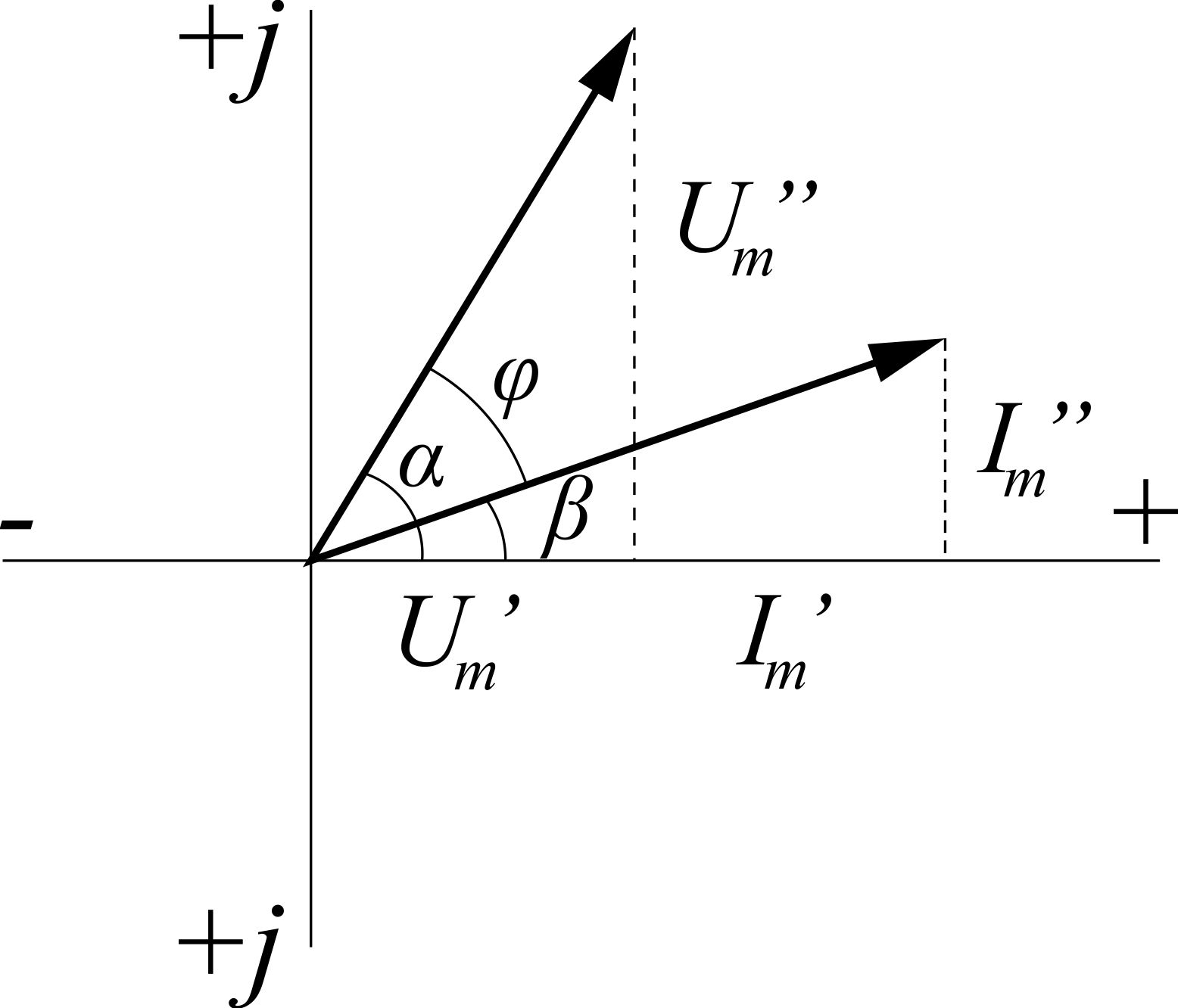
векторов на комплексной плоскости
|
1. Закон Ома. На рис. 3.37 изображены вектор напряжения
Ùm = Umеjα и вектор тока İm =Imеjβ. Здесь 
и β - начальные фазы напряжения и тока, определяемые выбором начала отсчета времени. Так как вектор тока отстает от вектора напряжения на угол φ< 90°, то ясно, что приемник, питаемый этим напряжением, содержит активное сопротивление и индуктивность.
Известно, что величина, равная отношению комплексной амплитуды напряжения, приложенного к приемнику, к комплексной амплитуде тока в приемнике называется комплексным сопротивлением. Обозначим комплексное сопротивление заглавной буквой:
(3.26)
Подставив вместо Ùm и İm их выражения, получим
где z — уже известное полное сопротивление цепи (модуль); а φ — фазовый угол между напряжением и током.
Таким образом, если напряжение на приемнике записать в комплексной форме, то, разделив комплексное выражение напряжения на комплексное сопротивление, получим комплексную величину, модуль которой равен току, а аргумент — фазовому углу между напряжением и током:
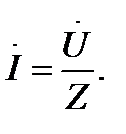(3.27)
Это и есть комплексная форма закона Ома.
2. Уравнения Кирхгофа. Согласно первому закону Кирхгофа алгебраическая сумма мгновенных значений токов в ветвях, связанных общим узлом электрической цепи, равна нулю:
. (3.28)
Мгновенные значения этих токов можно представить в виде вещественных или мнимых частей комплексных выражений İ1mejω, İ2mejω и т. д.
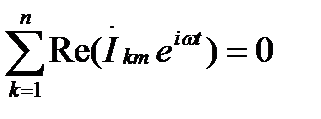(3.29)
. (3.30)
Так как равенство ∑ i = 0 справедливо при подстановке вместо мгновенных значений вещественных или мнимых частей комплексных выражений İkmejω, оно должно быть справедливым и при подстановке вместо мгновенных значений токов самих комплексных выражений İkmejω.
Действительно, умножив обе части равенства (3.30) на j и сложив равенства (3.29) и (3.30) получим
.
Таким образом, если вместо мгновенных значений токов в первое уравнение Кирхгофа подставить выражение İkmejω, равенство не нарушится.
Сократив обе части равенства на оператор вращения еjωt, получим первое уравнение Кирхгофа для амплитудных значений токов в комплексной форме:
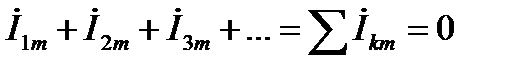. (3.31)
Подобное равенство можно написать и для действующих значений токов.
Таким образом, первый закон Кирхгофа можно сформулировать так: алгебраическая сумма комплексных выражений токов в ветвях, связанных общим узлом, равна нулю.
Для доказательства справедливости второго закона Кирхгофа в комплексной форме запишем для произвольного замкнутого контура уравнение, составленное согласно второму закону Кирхгофа для мгновенных значений э.д.с., и напряжений с учетом заданных и выбранных положительных направлений этих величин:
,
где k — номера ветвей, образующих замкнутый контур.
При синусоидальных э.д.с., генераторов и линейной цепи все мгновенные значения э.д.с., напряжений и токов можно представить в виде вещественных или мнимых частей комплексных величин: Ė1mejωt, Ė2mejωt,…, İ1mejωt, İ2mejωt.
Отметим, что амплитудные значения токов и э.д.с., и их начальные фазы не являются функциями времени и могут быть вынесены за знаки производных и интегралов. После подстановки получим
.
Разделим обе части равенства на оператор вращения
Если комплексное сопротивление каждой ветви контура обозначить буквой Zk, последнее уравнение примет более простой вид:
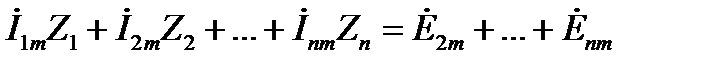
или
Для действующих значений это же уравнение запишется так:
.
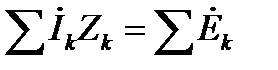Это и есть математическое, выражение второго закона Кирхгофа в комплексной форме.
Во всяком замкнутом контуре алгебраическая сумма комплексных выражений напряжений на отдельных элементах контура равна алгебраической сумме комплексных выражений э.д.с., действующих в этом контуре.