Резонанс в электрической цепи

 

Резонансом называют такой режим, при котором в цепи, содержащей реактивные сопротивления, ток совпадает по фазе с напряжением на зажимах цепи. Если в резонансе находится цепь, содержащая последовательно соединенные участки, имеющие индуктивный и емкостный характер, режим называется резонансом напряжений. Если в резонансе находится разветвленная цепь, содержащая параллельно соединенные участки, имеющие индуктивный и емкостный характер, режим называется резонансом токов.

Режим резонанса в технике электрической связи и автоматике играет чрезвычайно важную роль, поэтому он должен быть подробно исследован.

1. Последовательный колебательный контур. Электрическая цепь, схема которой изображена на рис. 3.38, называется последовательным колебательным контуром или просто последовательным контуром.

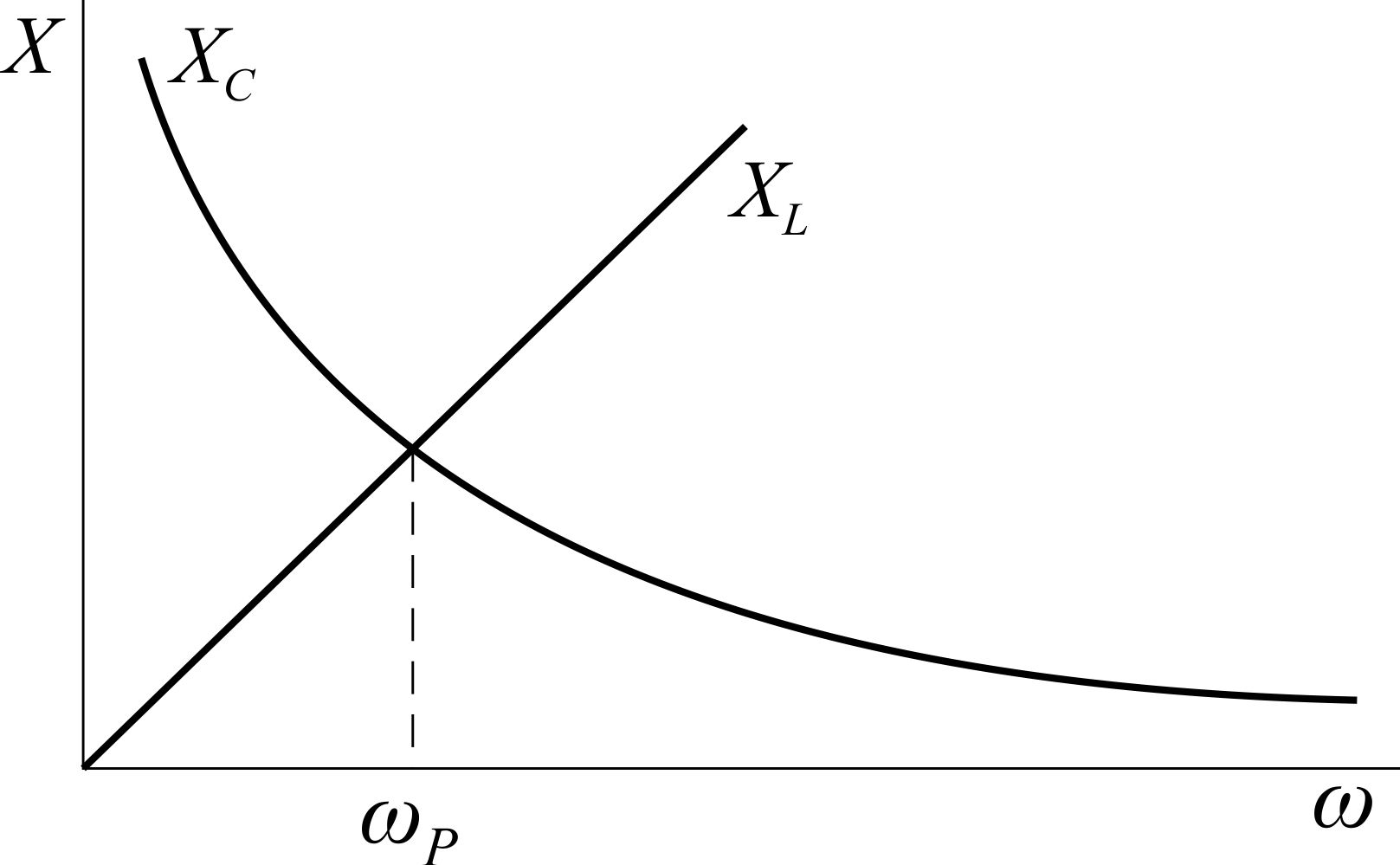Рис. 3.39. Изменение XC и XL

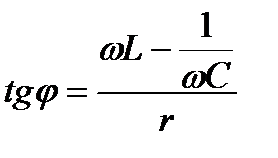Пусть последовательный контур подключен к источнику синусоидального напряжения и работает в режиме резонанса. При этом угол сдвига фаз между током и напряжением, приложенным к контуру, должен быть равен нулю (φ = 0). Из выражения видно, что ток в последовательном контуре может совпадать с напряжением по фазе при условии

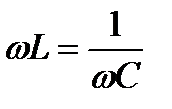. (3.35)

Это равенство, являющееся условием резонанса напряжений, говорит о том, что резонанса напряжений всегда можно добиться изменением в широких пределах индуктивности L, емкости С или частоты f приложенного к контуру напряжения. Если изменять, например, частоту f приложенного к контуру напряжения от 0 до ∞, то индуктивное сопротивление будет увеличиваться от x_L = 0 до x_L =∞ (рис. 3.39). При таком изменении fемкостное сопротивление х_C будет уменьшаться, принимая последовательно все возможные значения от x_C = ∞ до x_C = 0.

При некоторой частоте f_р сопротивления индуктивности и емкости окажутся одинаковыми:

.

Отсюда угловая резонансная частота

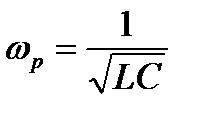(3.36)

и резонансная частота

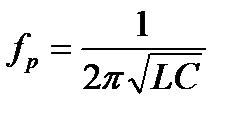. (3.37)

В дальнейшем, если параметры контура подобраны так, что его резонансная частота совпадает с частотой питающего напряжения, будем говорить, что контур настроен в резонанс с частотой питания.

Резонансную угловую частоту в общем случае электрической цепи условимся обозначать через ω_p.

Угловую частоту, равную 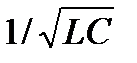, будем обозначать через ω₀:

.

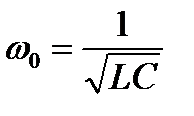Следовательно, угловая резонансная частота последовательного контура ω_p = ω₀. Индуктивному сопротивлению при резонансной частоте можно придать другой вид. Для этого вместо ω_p подставим ее выражение

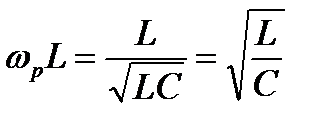. (3.38)

Емкостное сопротивление при резонансе можно представить в той же форме:

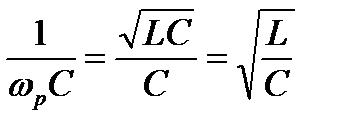. (3.39)

Рис. 3.40. Векторная диаграмма при резонансе напряжения

Эту величину, являющуюся важным параметром контура, называют характеристическим сопротивлением контура и обозначают буквой :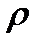

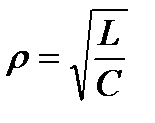. (3.40)

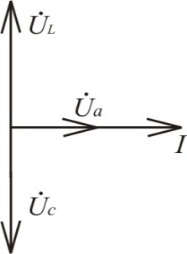
Векторная диаграмма последовательного контура рис. 3.38, работающего в режиме резонанса, изображена на рис. 3.40.

Так как x_L= x_C, то в этом режиме равны и напряжения на индуктивности и емкости. Комплексное сопротивление последовательного контура

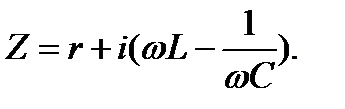
при резонансной частоте становится равным его активному сопротивлению: z=r.

Таким образом, контур при резонансе ведет себя как активное сопротивление.

Вся электромагнитная энергия, поступающая в контур, превращается в тепло и в генератор не возвращается. Мгновенная мощность такой цепи всегда положительна, несмотря на имеющиеся в цепи индуктивность и емкость.

При i=I_msinωt мгновенное значение энергии магнитного поля индуктивности определяется выражением

.

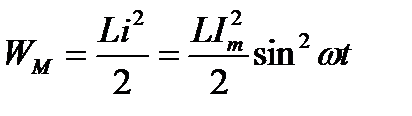Так как

,

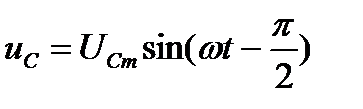мгновенное значение энергии электрического поля

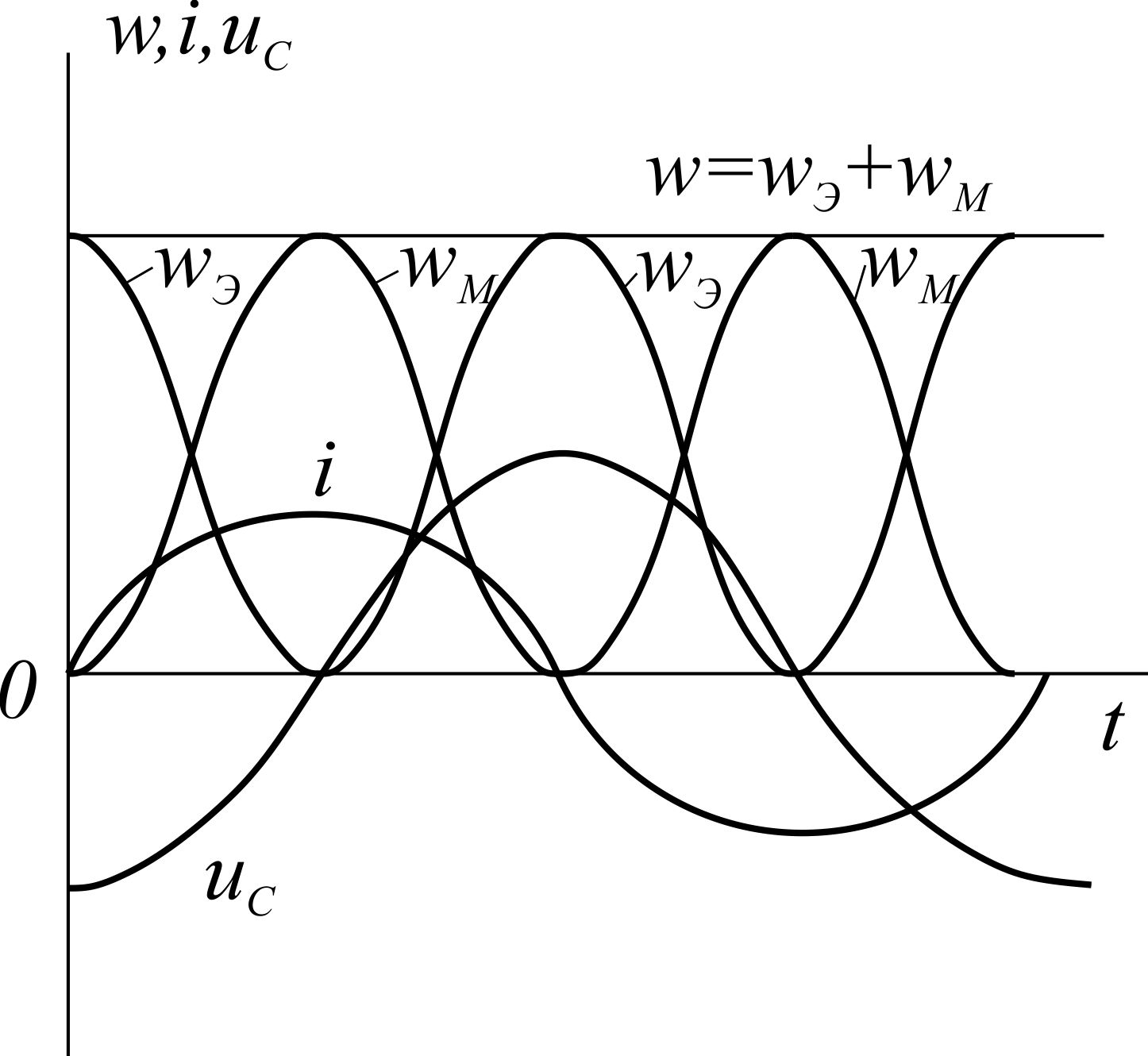Рис. 3.41. Колебание энергии в контуре

.

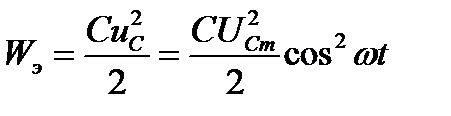Докажем, что при резонансе максимальные значения энергий магнитного и электрического полей одинаковы. Действительно,

.

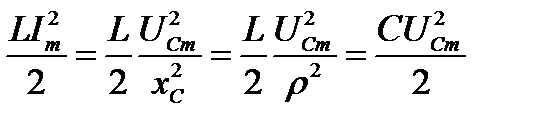Теперь можно доказать, что мгновенное значение общего запаса электромагнитной энергии последовательного контура при резонансе не является функцией времени; а представляет собой постоянную величину:

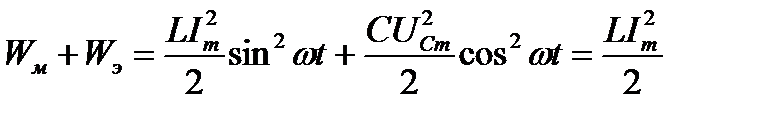. (3.41)

На рис. 3.41 построены кривая мгновенных значений тока в контуре, кривая мгновенных значений напряжения на конденсаторе и кривые Wэ и Wм. Ординаты горизонтальной прямой Wэ+Wм представляют собой мгновенные значения общего запаса электромагнитной энергии контура при резонансе. Этот запас энергии контура называется колебательной энергией контура.

Сравнивая между собой кривые Wэ и Wм видим, что в течение тех промежутков времени, когда Wм уменьшается, Wэ увеличивается и наоборот, а сумма их остается постоянной. Это говорит о том, что при резонансе напряжений происходит периодический обмен энергией между индуктивностью и емкостью. Когда индуктивность возвращает энергию в цепь, емкость ее забирает. Когда емкость отдает энергию, ее забирает индуктивность. У генератора же контур забирает за любой промежуток времени ровно столько энергии, сколько ее за это время превращается в тепло в активном сопротивлении. Колебаний энергии от генератора к приемнику и от приемника к генератору при этом не будет. Реактивная мощность, поступающая в цепь при резонансе, равна нулю.

Следует заметить, что все исследования нами проводятся при установившемся режиме работы цепи. Считаем, что запас электромагнитной энергии цепь получило после ее подключения к генератору, а момент подключения цепи к генератору был столь давно, что режим в цепи можно считать установившимся.

Для удобства дальнейшего исследования введем новые параметры контура, характеризующие его резонансные свойства.

Добротностью контура называют отношение характеристического сопротивления контура к его активному сопротивлению:

. (3.42)

Величина, обратная добротности контура, называется затуханием контура:

. (3.43)

Добротности контуров, используемых в высокочастотной практике, в зависимости от качества деталей колеблются для контуров среднего качества от 50 до 100, хорошего качеству — от 100 до 200, а контуров отличного качества добротность превышает 200. Последние используются главным образом в измерительных схемах.

Легко показать, что добротность контура определяет отношение запаса электромагнитной энергий контура при резонансе к энергии, поглощаемой в этом режиме активным сопротивлением контура за один период изменения тока в контуре. Действительно, колебательная энергия контура

.

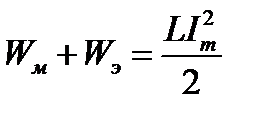Энергия, поглощаемая контуром в течение периода,

.

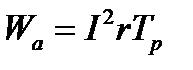Получаем

,

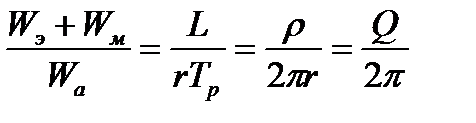откуда добротность контура

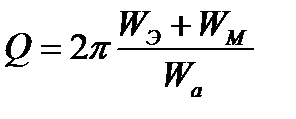. (3.44)

Это выражение является наиболее общим определением добротности колебательного контура любого вида.

2. Параллельный колебательный контур. Резонанс токов, как уже было сказано, может иметь место в цепи, содержащей параллельные ветви, имеющие индуктивный и емкостный характер. Такая цепь называется параллельным колебательным контуром или просто параллельным контуром (рис. 3.42). Так как под резонансом понимается такой режим, при котором общий ток совпадает по фазе с приложенным напряжением, находим условие резонанса токов из равенств φ = 0.

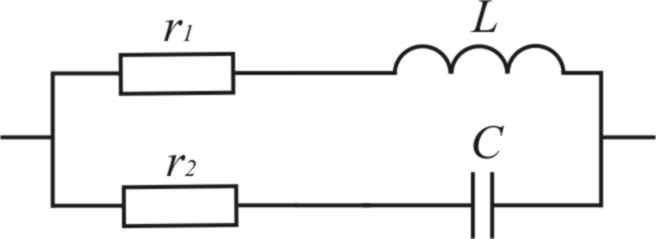Рис. 3.42. Резонанс токов

Для цепи, содержащей приемники в параллельном соединении,

.

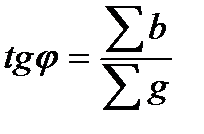В данном случае φ = 0 и поэтому ∑ b должна быть равна нулю. Отсюда условие резонанса токов

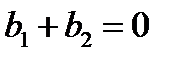,или .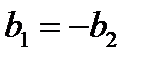

Таким образом, при резонансе токов реактивная проводимость ветви с индуктивной реакцией должна равняться реактивной проводимости ветви с емкостной реакцией с обратным знаком. Из равенства реактивных проводимостей ветвей следует равенство модулей реактивных составляющих токов в этих ветвях и противоположность их фаз

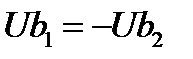или .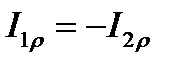

На основании равенства токов можно утверждать, что векторная диаграмма рис. 3.43, где I₁ и I₂ — токи в параллельных ветвях некоторой цепи, свидетельствует о том, что цепь находится в режиме резонанса, несмотря на резкую разницу токов в ветвях. Так как реактивная составляющая общего тока равна нулю, вектор общего тока совпадает по направлению с вектором напряжения.

Воспользовавшись переходными формулами, перепишем условие резонанса для цепи рис. 3.42. Так как

, ,

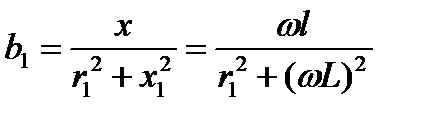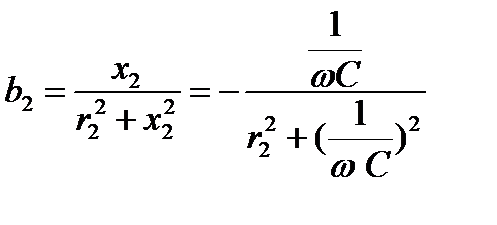то

.

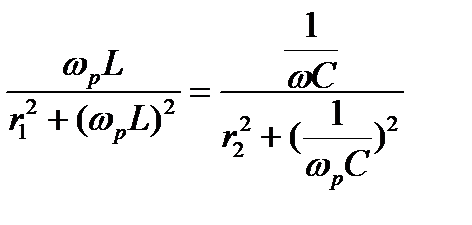Решаем это равенство относительно ωр и находим резонансную частоту:

Рис. 3.43. Векторная диаграмма при резонансе токов

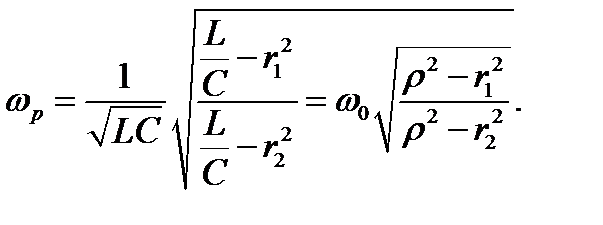(3.45)

Из выражений резонансной частоты следует, что при равенстве активных сопротивлений ветвей r₁ = r₂≠ ρ и при r₁<<ρ и r₂<<ρ резонансная частота

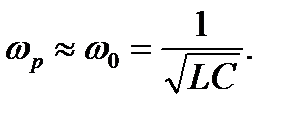(3.46)

В этом случае условие резонанса токов совпадает с условием резонанса напряжений.

При r₁>ρ и одновременно r₂<ρ или при r₁< ρ и r₂>ρ ни при какой частоте резонанс не наступает.

При r₁>ρ и r₂>ρ или при r₁<ρ и r₂<ρ резонанс наступает при частоте, равной ω_р.

В частном случае подобранного равенства r₁ = r₂ = р, резонансная частота является неопределенной, она может иметь любое значение. Это означает, что при любой частоте общий ток и приложенное к цепи напряжение совпадают по фазе. Последний, специальный, случай равенства параметров контура в технике связи не используется, так как в контурах связи r << ρ.