В предыдущем параграфе было показано, что уравнения Кирхгофа в алгебраической форме при выбранных положительных направлениях токов и напряжений справедливы и для цепей синусоидального переменного тока в том случае, если сопротивления всех элементов цепей, все действующие (или амплитудные) значения токов, напряжений и э.д.с., записаны в комплексной форме. Поэтому можно утверждать, что все методы расчета линейных цепей при постоянном токе могут быть использованы при расчетах линейных цепей при синусоидальном переменном токе в том случае, если сопротивления всех элементов цепей, действующие (или амплитудные) значения токов, напряжений и э.д.с., записаны в комплексной форме.
Доказательства справедливости этих методов расчета и выводов расчетных формул здесь не приводятся. Это было бы повторением изложенного выше материала с той только разницей, что вместо r, g и Е, U, I для цепей постоянного тока при расчете линейных цепей при синусоидальном переменном токе символическим методом следует писать Z, Y и Ė, Ù, İ соответственно.
Таким образом, введя вместо векторов отображающие их комплексные выражения, получаем возможность расчета цепей переменного тока всеми методами расчета сложных цепей, рассмотренными выше. Все заданные э.д.с., напряжения или токи должны быть записаны в комплексной форме с учетом выбранных и нанесенных на схему их положительных направлений. Положительное направление напряжения на любом двухполюснике, как правило, выбирается совпадающим с положительным направлением тока. Одна из заданных функций времени может быть записана с начальной фазой, равной нулю, т. е. в виде вещественного числа.
|
|
1. Метод контурных токов. Рассчитывая сложную цепь методом контурных токов, уравнения Кирхгофа для контурных токов в общем случае n-контурной схемы необходимо записать в следующей форме:
, (3.32)
здесь İkk - контурный ток k-го контура; Zkk = rkk + jxkk - комплексное сопротивление k-го контура и Znk = Zkn = rnk + jxnk — сопротивление, общее для k-го и п-го контуров. Сопротивление Znk в уравнение следует записать со своим знаком, если контурные токи İпп и İkk направлены через это сопротивление согласно. При встречных положительных направлениях смежных токов через общие сопротивления Znk эти сопротивления в уравнения следует записывать с обратными знаками. Ekk - сумма действующих в k-м контуре э.д.с., записанных в комплексной форме. В сумму входят со знаком плюс э.д.с., положительные направления, которых совпадают с выбранным направлением обхода контура.
Следует повторить, что перед расчетом цепи любым методом необходимо на схему нанести заданные или выбранные положительные направления э.д.с., и токов.
2. Метод узловых напряжений. При расчете цепи методом узловых напряжений уравнения для узловых напряжений относительно опорного узла с потенциалом φо = 0 для цепи, содержащей n + 1 узел, имеют вид:
, (3.33)
| Рис. 3.38. Ветвь сложной электрической цепи |
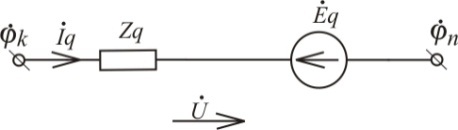здесь Ykk - сумма полных проводимостей ветвей, сходящихся в узле k; Ynk = Ykn — сумма полных проводимостей ветвей, непосредственно связывающих узлы п и k, взятая со знаком минус; ∑kĖqYq—сумма произведений э.д.с., на проводимости соответствующих ветвей, сходящихся в узле k. Отдельные слагаемые этой суммы записываются со знаком плюс, если положительное направление э.д.с., в ветви задано к узлу k, и со знаком минус, если положительное направление э.д.с., задано от узла k независимо от выбранного положительного направления тока в ветви. Напряжения узлов относительно опорного можно найти с помощью формул, подобных формуле (2.9,а). Ток в ветви q,связывающей узлы k и n (рис. 3.38), определяется из уравнения|
|
,
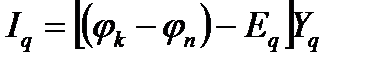где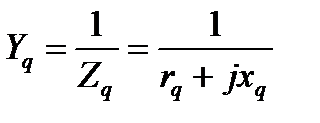 
- полная проводимость ветви.
Знаки в выражении İq написаны в соответствии с положительными направлениями İq, 
, и Ėq на рис. 3.38, где изображена одна из ветвей сложной электрической цепи. В частном случае потенциал одного из узлов k или п может быть принят равным нулю.
Для цепи, содержащей всего два узла и n ветвей, напряжение первого узла относительно второго (опорного), потенциал которого принят равным нулю, определяется из равенства:
.
3. Преобразование треугольника в эквивалентную звезду. Формулы преобразования сторон треугольника в лучи эквивалентной звезды в комплексной форме подобны при постоянном токе. Например, для узла а (см. рис.2.24)
.
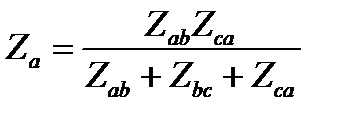Следует отметить, что вещественная часть Za может оказаться отрицательной. Такое сопротивление в пассивной линейной электрической цепи создать невозможно. При расчете цепей любым другим методом отрицательная вещественная часть сопротивления или проводимости могла быть получена только в результате ошибки в расчете. При расчете же методом преобразования треугольника в эквивалентную звезду отрицательная вещественная часть свидетельствует лишь о том, что замена реального треугольника эквивалентной реальной звездой физически невозможна. С расчетной же точки зрения это преобразование возможно и расчет может быть продолжен.
|
|
4. Метод эквивалентного генератора. Метод наложения. При расчете сложной электрической цепи методом эквивалентного генератора напряжения искомый ток в ветви определяется согласно закону Ома:
,
где э.д.с., эквивалентного генератора Ėэ.г и его внутреннее сопротивление Zэ.г определяются так же, как и при расчете цепей при постоянном токе.
Расчет цепей методом эквивалентного генератора тока, методом наложения и другим любым методом принципиально не отличается от расчета подобных цепей постоянного тока. Для расчета сложной цепи любым из перечисленных методов все сопротивления ветвей следует записывать в комплексной форме. Все э.д.с., генераторов или их задающие токи необходимо записывать в комплексной форме с учетом начальных фаз этих синусоидальных функций времени. В каждой ветви нужно указывать положительные направления заданных токов, э.д.с., выбранные положительные направления искомых токов и напряжений.
Для исследования цепей может быть использован принцип дуальности.
При преобразованиях исходных цепей в дуальные, при замене всех величин дуальными сопротивления ряда последовательных элементов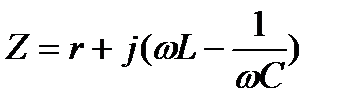 
преобразуются в проводимость параллельного соединения: 
.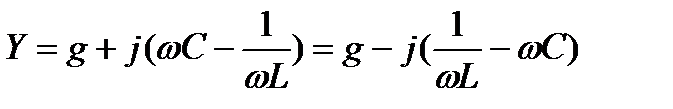