Последовательное соединение r, L и С

При синусоидальном токе

 

1. Временная и векторная диаграммы. Треугольники напряжений и сопротивлений. После исследования цепи, содержащей только активное сопротивление, или индуктивность, или емкость, рассмотрим цепь, содержащую активное сопротивление, индуктивность и емкость в последовательном соединении.

На основании второго уравнения Кирхгофа для цепи, содержащей r, L и С в последовательном соединении (рис. 3.11), можно записать

Рис. 3.11. Последовательное соединение r, L, C

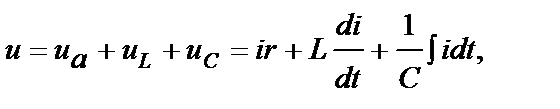(3.5)

где - мгновенное значение напряжения на активном сопротивлении; - мгновенное значение напряжения на индуктивности; - мгновенное значение напряжения на емкости; и - мгновенное значение приложенного к цепи напряжения.

Второе уравнение Кирхгофа в виде уравнения (3.5) справедливо при токе любой формы и, в частности, при синусоидальном токе.

Рис. 3.12. Синусоиды мгновенных значений тока и напряжений

В этом случае напряжения на активном сопротивлении, индуктивности и емкости как было показано, также будут синусоидальными функциями времени. А так как алгебраическая сумма синусоидальных функций одинаковой частоты есть синусоидальная функция той же частоты (см. § 3.2), следует заключить, что синусоидальный ток в линейной цепи, содержащей r, L и С, может быть в том случае, если к цепи приложено синусоидальное напряжение.

Полагая ток в цепи , найдем амплитуду U_m и начальную фазу φ приложенного к цепи напряжения . Для этого можно построить синусоиду тока в цепи и синусоиды напряжения на отдельных приемниках .

На рис. 3.12 построены синусоида тока в рассматриваемой цепи, синусоида напряжения на активном сопротивлении 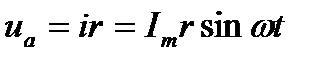, синусоида напряжения на индуктивности и синусоида напряжения на емкости

Для получения кривой приложенного ко всей цепи напряжения следовало бы для каждого момента времени сложить ординаты кривых U _a, U _L и U _C. Кривая, ординаты которой в любой момент времени равны алгебраической сумме ординат U _a + U _L+ U _C, будет кривой приложенного напряжения.

Так как напряжение на индуктивности опережает ток по фазе на Т/4, а напряжение на емкости отстает от тока по фазе на Т/4, напряжения на индуктивности и на емкости сдвинуты между собой на полпериода и находятся в противофазе. Суммарное напряжение на индуктивности и емкости при их последовательном соединении называется реактивным напряжением и обозначается Up:

или

Рис. 3.13. Синусоиды составляющих мгновенных напряжений

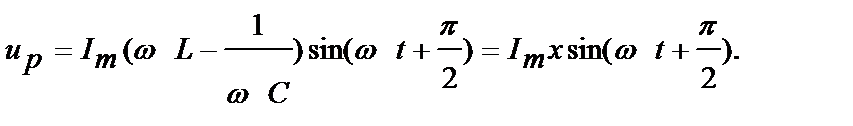
Таким образом, I_mx есть амплитуда реактивного напряжения, а реактивное сопротивление цепи, содержащей L и С в последовательном соединении. На рис. 3.13 построены кривые тока i, активного Ua, реактивного иp и приложенного ко всей цепи напряжений u = u_а + u_р. Задачу определения и φ проще решить графическим путем помощью векторной диаграммы. Для получения мгновенного значения приложенного к цепи напряжения, мгновенные значения напряжения на отдельных последовательно соединенных участках цепи должны быть сложены алгебраически. Для получения амплитуды приложенного напряжения амплитудные значения напряжений на этих участках необходимо сложить геометрически.

Рис. 3.14. Треугольник напряжений (первый вид)

ULm Um φ Uрm 0 Uam Im UCm

Необходимость геометрического сложения амплитудных значений напряжений на отдельных участках цепи обусловлена тем, что напряжения на различных участках при одном и том же токе в них достигают амплитудных значений разновременно. Сдвиг во времени между синусоидально изменяющимися величинами соответствует повороту векторов, отображающих эти синусоидально изменяющиеся величины, на векторной диаграмме одного относительно другого на углы, равные разностям фаз между отображаемыми ими синусоидами. Построим векторную диаграмму для цепи, содержащей в последовательном соединении r, L и С, откладывая в виде векторов амплитудные значения тока и напряжений. Последовательное соединение характеризуется одним и тем же током в приемниках, поэтому построение начнем с вектора тока, общего для всех приемников. Отложим из произвольной точки вектор, равный в масштабе тока амплитудному значению тока в цепи (рис. 3.14). Начальную фазу одной из синусоидальных функций времени — тока, напряжения или э.д.с., - можно выбрать произвольно.

При этом начальные фазы остальных синусоидальных функций будут определяться фазовым сдвигом этих функций относительно первой. Уравнение тока написано с начальной фазой тока, равной нулю, поэтому вектор тока I_m откладываем в направлении горизонтальной оси. Напомним, что мгновенное значение синусоидальных функций времени условились определять как проекции вращающихся векторов на ось ординат.

Уже указывалось, что при построении векторных диаграмм отсчет углов в положительном направлении производится против движения часовой стрелки, так как за положительное направление вращения векторов принято направление, противоположное направлению вращения часовой стрелки.

Вектор U_am=I_тr, изображающий напряжение на активном сопротивлении, должен совпадать по направлению с вектором тока. Вектор U_Lm=I_mx_L, изображающий напряжение на индуктивности, строим из начала координат (точки 0) вертикально вверх, так как напряжение на индуктивности опережает ток по фазе на π/2. Вектор, равный напряжению на емкости U_Сm = I_mx_C, строим также из начала координат, но вертикально вниз. Он отстает от вектора тока на π/2, так как на этот угол напряжение на емкости отстает по фазе от тока через емкость. Таким образом, вектор U_Lm и вектор U_Cm оказались сдвинутыми между собой на угол в 180°. Уже отмечалось, что напряжения на индуктивности и на емкости при последовательном их включении находятся в противофазе.

Вектор суммарного напряжения на индуктивности и емкости может быть найден как геометрическая сумма векторов:

.

При построении диаграммы амплитуда напряжения на индуктивности U_Lт выбрана большей, чем амплитуда напряжения на емкости U_Cm. Это соответствует тому, что в исследуемой цепи х_L>х_C. Сложив геометрически вектор U_аm с вектором U_pm, получим вектор, изображающий амплитуду приложенного к цепи напряжения. Получившийся прямоугольный треугольник с катетами U_am и U_pm получил название треугольника напряжений.

ULm Um Uрm φ Uam Im UCm   Рис. 3.15. Треугольник напряжений (второй вид)

Для исключения из векторной диаграммы вспомогательных построений векторы U_Lm и U_Cm можно строить не из начала координат, а из конца вектора U_am как показано на топографической диаграмме рис. 3.15. Топографическими векторными диаграммами называют такие, в которых расположение векторов напряжений на элементах цепи соответствует расположению самих элементов цепи в схеме. При этом каждая точка диаграммы отображает определенную точку схемы. Рассматривая снова треугольник напряжений, находим амплитуду напряжения, проложенного ко всей цепи:

здесь U_am —амплитуда активной составляющей напряжения, или активного напряжения; U_pm — амплитуда реактивной составляющей напряжения, или реактивного напряжения. Подставляя в последнее равенство значения U_аm и U_pm, получим

где x = 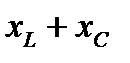— реактивное сопротивление цепи.

Полное сопротивление цепи, определяемое как Um/Im или U/I,обозначается буквой z:

(3.6)

Разделив все стороны треугольника напряжений на ток, получим треугольник сопротивлений (рис. 3.16). Катетами треугольника сопротивлений являются активное r и реактивное х сопротивления цепи, а гипотенузой — полное сопротивление цепи z. Стороны треугольника сопротивлений не являются векторами, однако, обозначаем их со стрелками, указывающими положительные направления напряжений на этих сопротивлениях.

Um z x φ r Im

Рис. 3.16. Треугольник сопротивлений

Из треугольника сопротивлений следуют соотношения, позво­ляющие определить угол сдвига фаз φ между напряжением, прило­женным к цепи, и током в цепи:

(3.7)

Из этих формул очевидно, что угол сдвига между напряжением на зажимах последовательной цепи и током в этой цепи зависит только от соотношения между сопротивлениями отдельных элементов этой цепи.

При изменении частоты приложенного напряжения индуктивное x_L= ωL и емкостное x_C = 1/ωС сопротивления также изменяются, а вместе с ними изменится и угол φ.

Независимо от величин ωL и 1/ωС под реактивным сопротивлением х условились понимать разность между индуктивным и емкостным сопротивлениями:

Поэтому, когда x_L>x_C, положительны х и φ, цепь носит индук­тивный характер, т. е. обладает индуктивной реакцией. При этом ток отстает по фазе от приложенного напряжения. Если же x_L<x_C, то реактивное сопротивление цепи х и угол φ отрицательны, характер цепи емкостный, т. е. цепь обладает емкостной реакцией. В такой цепи ток опережает по фазе напряжение, приложенное ко всей цепи.

 

 

Рис. 3.17. Режимы блоков электрической цепи

 

Следует подчеркнуть, что активное сопротивление r, индуктивное сопротивление x_L и емкостное x_C — величины положительные. Реактивное же сопротивление х может быть и положительным, и отрицательным. Например, реактивное сопротивление ветви, содержащей только конденсатор, отрицательно: х = - x_С.

Из условия х = x_L-x_C вытекает, что если уравнение напряжения написано в виде , а уравнение тока

,

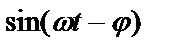то в любом конкретном случае последовательной цепи вместо φ следует подставлять фазовый угол со своим знаком. Так, для цепи рис. 3.17 напряжение на первом приемнике опережает ток по фазе (φ₁> 0), на втором приемнике напряжение отстает от тока по фазе (φ₂< 0) и

φ₃>0 для третьего приемника (напряжение опережает ток по фазе). Судя по топографической векторной диаграмме (рис. 3.18), напряжение, приложенное ко всей цепи, опережает ток по фазе.

Следовательно,

и

Знак фазового угла между напряжением и током можно определить, если его отсчитывать от вектора тока. В случае индуктивной нагрузки, когда вектор напряжения опережает вектор тока, этот угол отсчитывается в направлении отсчета положительных углов, т. е. против движения часовой стрелки. При емкостной нагрузке, когда ток опережает по фазе напряжение, угол φ от вектора тока отсчитывается в направлении движения часовой стрелки, и он окажется отрицательным.

Рис. 3.18. Топографическая диаграмма

2. Схема замещения катушки и конденсатора. Схема замещения реальной катушки в тех случаях, когда емкостью обмотки можно пренебречь, может быть представлена в виде индуктивности и активного сопротивления, соединенных последовательно. Отношение индуктивного сопротивления катушки к ее активному сопротивлению ωL/r называется добротностью катушки . Как видно из формулы, добротность катушки зависит от частоты. С увеличением частоты добротность катушки возрастает. Однако возрастание добротности с переходом частоты в область высоких частот становится незначительным из-за роста эквивалентного активного сопротивления катушки.

Схема замещения реального конденсатора обычно представляет собой емкость и активное сопротивление, соединенные параллельно. В такой схеме замещения добротность конденсатора