1. Сопротивления. Отношение комплексного напряжения к комплексному току называется комплексным сопротивлением

 (3.17)
(3.17)
где  - отношение действующего или амплитудного напряжения соответственно к действующему или амплитудному току называется полным сопротивлением. Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т.е.
- отношение действующего или амплитудного напряжения соответственно к действующему или амплитудному току называется полным сопротивлением. Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т.е. 
Комплексное сопротивление можно представить в виде
 ,
,
где  - вещественная часть комплексного сопротивления, называется активным сопротивлением;
- вещественная часть комплексного сопротивления, называется активным сопротивлением;
 - значение мнимой части комплексного сопротивления, называется реактивным сопротивлением.
- значение мнимой части комплексного сопротивления, называется реактивным сопротивлением.
Очевидно, что

 ,
, 
 .
.
В технической литературе встречаются также следующие наименования для сопротивлений: вместо полного сопротивления – кажущееся сопротивление, импеданс; вместо комплексного сопротивления – комплексный импеданс, вместо реактивного сопротивления – реактанс.
Для схемы, представленной на рис. 3.11, комплексное сопротивление

Напомним, что реактивное сопротивление

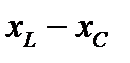 , (3.18)
, (3.18)
где  являются соответственно индуктивным и емкостным сопротивлениями.
являются соответственно индуктивным и емкостным сопротивлениями.
В свою очередь индуктивное сопротивление связывает между собой амплитуды напряжения на индуктивности и тока:
 ;
;  .
.
Индуктивное сопротивление прямо пропорционально частоте тока. Это объясняется тем, что напряжение на индуктивности пропорционально скорости изменения тока: 

Емкостное сопротивление связывает между собой амплитуды напряжения на емкости и тока:
 ;
;  .
.
Емкостное сопротивление обратно пропорционально частоте тока. Эту зависимость от частоты легко пояснить, а искомой величиной ток:  Ток прямо пропорционален скорости изменения напряжения на зажимах емкости и, следовательно, емкостное сопротивление обратно пропорционально частоте напряжения.
Ток прямо пропорционален скорости изменения напряжения на зажимах емкости и, следовательно, емкостное сопротивление обратно пропорционально частоте напряжения.
Напряжения на последовательно соединенных индуктивности и емкости противоположны по фазе; поэтому в выражение (3.18) для реактивного сопротивления x сопротивления 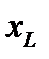 и
и 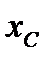 входят с различными знаками. Напряжения на индуктивности и на емкости сдвинуты по фазе относительно напряжения на сопротивлении соответственно на p/2 и -p/2. Поэтому эти сопротивления входят в Z как
входят с различными знаками. Напряжения на индуктивности и на емкости сдвинуты по фазе относительно напряжения на сопротивлении соответственно на p/2 и -p/2. Поэтому эти сопротивления входят в Z как 

 и
и  при переходе от дифференциальной формы, параметризованной временем, к символической, представленной положением вектора на комплексной плоскости при фиксированном значении времени.
при переходе от дифференциальной формы, параметризованной временем, к символической, представленной положением вектора на комплексной плоскости при фиксированном значении времени.
Напомним, что индуктивное и емкостное сопротивления являются величинами арифметическими – положительными, а реактивное сопротивление  - величина алгебраическая и может быть как больше, так и меньше нуля.
- величина алгебраическая и может быть как больше, так и меньше нуля.
Для ветви, содержащей только индуктивность, реактивное сопротивление x равно индуктивному сопротивлению  , а реактивное сопротивление x ветви, содержащей только емкость, равно емкостному сопротивлению, взятому со знаком минус, т.е.
, а реактивное сопротивление x ветви, содержащей только емкость, равно емкостному сопротивлению, взятому со знаком минус, т.е.  .
.
Заметим также, что для ветвей, каждая из которых содержит только сопротивление r, только индуктивность L или только емкость C, комплексные сопротивления соответственно равны:

2. Разность фаз напряжения и тока. Условимся под разностью фаз j напряжения и тока понимать разность начальных фаз напряжения 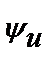 и тока
и тока 
 (3.19)
(3.19)
Поэтому на векторной диаграмме угол j отсчитывается в направлении от вектора  к вектору
к вектору 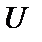 (рис. 3.16). Именно при таком определении разности фаз угол j равен аргументу комплексного сопротивления. Угол j положителен при отстающем токе (
(рис. 3.16). Именно при таком определении разности фаз угол j равен аргументу комплексного сопротивления. Угол j положителен при отстающем токе (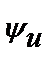 >
> 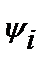 ) и отрицателен при опережающем токе (
) и отрицателен при опережающем токе ( <
<  ).
).
Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При  >
> 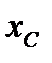 имеем
имеем  >0 и ток отстает по фазе от напряжения,
>0 и ток отстает по фазе от напряжения,  .При
.При  имеем
имеем  ,
, 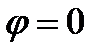 ,
,  ток совпадает по фазе с напряжением. В целом проявляет себя как активное сопротивление. Это случай так называемого резонанса, который подробно рассматривается в § 3.14. Наконец, при
ток совпадает по фазе с напряжением. В целом проявляет себя как активное сопротивление. Это случай так называемого резонанса, который подробно рассматривается в § 3.14. Наконец, при 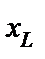 <
<  имеем x<0, j<0, ток опережает по фазе напряжения.
имеем x<0, j<0, ток опережает по фазе напряжения.
Векторные диаграммы для трех возможных соотношений 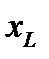 и
и  даны на рис. 3.33. При построении этих диаграмм начальная фаза тока yi принята равной нулю. Поэтому j и yu равны друг другу.
даны на рис. 3.33. При построении этих диаграмм начальная фаза тока yi принята равной нулю. Поэтому j и yu равны друг другу.
Рассматривая при заданной частоте цепь по рис. 3.11 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при  как последовательное соединение сопротивления и индуктивности (r и
как последовательное соединение сопротивления и индуктивности (r и  ), при
), при  как сопротивление r и при
как сопротивление r и при  <
<  как последовательное соединение сопротивления и емкости (r и
как последовательное соединение сопротивления и емкости (r и  ). При заданных L и C соотношение между
). При заданных L и C соотношение между 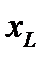 и
и  зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
 Рис. 3.33. Векторные диаграммы (последовательное соединение)
Рис. 3.33. Векторные диаграммы (последовательное соединение)
|
 . Тогда, как следует из (3.19), начальная фаза тока yiравна и противоположна по знаку разность фаз j, т.е.
. Тогда, как следует из (3.19), начальная фаза тока yiравна и противоположна по знаку разность фаз j, т.е. 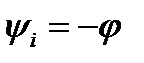 .
.
3. Проводимости. Отношение комплексного тока к комплексному напряжению называется комплексной проводимостью
 (3.20)
(3.20)
где  - величина, обратная полному сопротивлению, называется полной проводимостью.
- величина, обратная полному сопротивлению, называется полной проводимостью.
Комплексная проводимость и комплексное сопротивление взаимообратные. Комплексную проводимость можно представить в виде
 (3.21)
(3.21)
где  - вещественная часть комплексной проводимости, называется активной проводимостью;
- вещественная часть комплексной проводимости, называется активной проводимостью;
 - значение мнимой части комплексной проводимости, называется реактивной проводимостью;
- значение мнимой части комплексной проводимости, называется реактивной проводимостью;
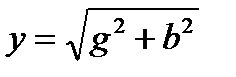 ;
; 
В технической литературе встречаются также следующие наименования для проводимостей: вместо полной проводимости – кажущаяся проводимость, адмиттанс; вместо комплексной проводимости – комплексный адмиттанс.
Для схемы, представленной на рис. 3.20, комплексная проводимость
 ,
,
где
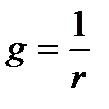 ,
,  ,
, 
и являются соответственно активной, индуктивной и емкостной проводимостями.
Реактивная проводимость
 . (3.22)
. (3.22)
Индуктивная  и емкостная
и емкостная  проводимости – арифметические величины, а реактивная проводимость (b) – алгебраическая величина и может быть как больше, так и меньше нуля. Реактивная проводимость b ветви, содержащей только индуктивность, равна индуктивной проводимости
проводимости – арифметические величины, а реактивная проводимость (b) – алгебраическая величина и может быть как больше, так и меньше нуля. Реактивная проводимость b ветви, содержащей только индуктивность, равна индуктивной проводимости  , а реактивная проводимость bветви, содержащей только емкость, равна емкостной проводимости с обратным знаком, т.е.
, а реактивная проводимость bветви, содержащей только емкость, равна емкостной проводимости с обратным знаком, т.е. 
 Рис. 3.34. Векторные диаграммы (параллельное соединение)
Рис. 3.34. Векторные диаграммы (параллельное соединение)
|
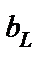 >
> 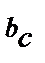 ,
,  =
= 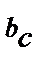 и
и 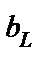 <
< 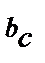 . При построении этих диаграмм начальная фаза напряжений принята равной нулю, поэтому j и
. При построении этих диаграмм начальная фаза напряжений принята равной нулю, поэтому j и  как это следует из (3.19), равны и противоположны по знаку
как это следует из (3.19), равны и противоположны по знаку 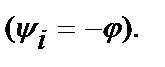
Рассматривая схему по рис. 3.20 в целом как пассивный двухполюсник, можно заметить, что при заданной частоте она эквивалентна в первом случае параллельному соединению проводимости и индуктивности. Во втором – проводимости и в третьем – параллельному соединению проводимости и емкости. Второй случай называется резонансом и рассматривается в § 3.14. При заданных L и C соотношение между  и
и  зависит от частоты, а поэтому от частоты зависит и вид эквивалентной схемы.
зависит от частоты, а поэтому от частоты зависит и вид эквивалентной схемы.
Обратим внимание на то, что в схеме рис. 3.20 каждая из параллельных ветвей содержит по одному элементу. Поэтому получилось такое простое выражение для Y, в которое проводимости элементов входят как отдельные слагаемые.
В общем случае
 (3.23)
(3.23)
откуда

 (3.24)
(3.24)
и, наоборот,

 (3.25)
(3.25)
Из полученных соотношений видно, что b и x всегда имеют одинаковый знак.
Наоборот, для схемы на рис. 3.20, состоящей из параллельного соединения элементов, получаются простые выражения для проводимостей, но относительно сложные выражения для сопротивлений, причем и эквивалентное и активное сопротивление зависит от частоты:


Переход от сопротивления  к проводимости
к проводимости  и обратно соответствует замене схемы цепи с последовательным соединением элементов r и x эквивалентной схемой с параллельным соединением элементов g и b и обратно.
и обратно соответствует замене схемы цепи с последовательным соединением элементов r и x эквивалентной схемой с параллельным соединением элементов g и b и обратно.
Заметим, что обозначения Z, Y, r,  ,
,  ,
,  , g, b,
, g, b,  и
и  применяются не только для сопротивлений и проводимостей, но и для элементов схемы, характеризуемых этими величинами. В таких случаях элементам схемы дают те же самые наименования, какие присвоены величинам, которые обозначаются этими буквами.
применяются не только для сопротивлений и проводимостей, но и для элементов схемы, характеризуемых этими величинами. В таких случаях элементам схемы дают те же самые наименования, какие присвоены величинам, которые обозначаются этими буквами.
Комплексные сопротивления или проводимости как элементы схемы имеют условное обозначение в виде прямоугольника (рис. 3.16, рис. 3.22).
4. Пассивный двухполюсник. Ток и напряжение на входе любого пассивного двухполюсника (рис. 3.35) связаны законом Ома
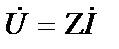 и
и 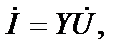
 Рис. 3.35. Пассивный двухполюсник
Рис. 3.35. Пассивный двухполюсник
|
Входному комплексному сопротивлению  соответствует эквивалентная схема двухполюсника, состоящая из последовательного соединения активного сопротивления r и реактивного сопротивления x.
соответствует эквивалентная схема двухполюсника, состоящая из последовательного соединения активного сопротивления r и реактивного сопротивления x.
Последнее в зависимости от знака следует рассматривать либо как индуктивное, либо как емкостное сопротивление.
Напряжение  можно разложить на составляющие:
можно разложить на составляющие:

где  - составляющая, совпадающая по фазе с током, является активной составляющей напряжения;
- составляющая, совпадающая по фазе с током, является активной составляющей напряжения;
 - составляющая, сдвинутая по фазе относительно тока на угол p/2, является реактивной составляющей напряжения.
- составляющая, сдвинутая по фазе относительно тока на угол p/2, является реактивной составляющей напряжения.
Составляющие  и
и  можно рассматривать как напряжения на элементах r и x эквивалентной схемы.
можно рассматривать как напряжения на элементах r и x эквивалентной схемы.
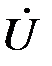 ,
, 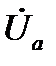 и
и 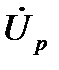 со сторонами, пропорциональными z, r и
со сторонами, пропорциональными z, r и 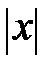 , является треугольником напряжений. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны сопротивлениям z, r и
, является треугольником напряжений. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны сопротивлениям z, r и 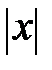 , очевидно будет треугольником сопротивлений. Из треугольника напряжений следует, что
, очевидно будет треугольником сопротивлений. Из треугольника напряжений следует, что
 ,
,  ,
,  .
.
Входной комплексной проводимости  соответствует эквивалентная схема двухполюсника, состоящего из параллельного соединения проводимостей g и b. Последняя в зависимости от знака либо индуктивная, либо емкостная.
соответствует эквивалентная схема двухполюсника, состоящего из параллельного соединения проводимостей g и b. Последняя в зависимости от знака либо индуктивная, либо емкостная.
Ток на входе двухполюсника можно разложить на составляющие:
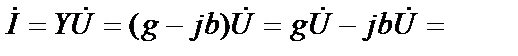
 ,
,
где  - составляющая, совпадающая по фазе с напряжением, является активной составляющей тока;
- составляющая, совпадающая по фазе с напряжением, является активной составляющей тока;
 - составляющая, сдвинутая по фазе относительно напряжения на угол p/2, является реактивной составляющей тока.
- составляющая, сдвинутая по фазе относительно напряжения на угол p/2, является реактивной составляющей тока.
Составляющие 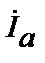 и
и  можно рассматривать как токи в элементах g и b эквивалентной схемы.
можно рассматривать как токи в элементах g и b эквивалентной схемы.
Треугольник, образованный векторами  ,
,  , и
, и  (рис. 3.36), со сторонами, пропорциональными y, g,
(рис. 3.36), со сторонами, пропорциональными y, g,  , будет треугольником токов.
, будет треугольником токов.
Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны проводимостям y, g и  , следует считать треугольником проводимостей.
, следует считать треугольником проводимостей.
Из треугольника токов имеем:

 ;
; 
 ;
; 
5. Комплексная мощность. Если известны напряжение и ток в двухполюснике в комплексной форме, можно определить мощность, поступающую в него. При этом напрашивается мысль, что для этого следует комплексное напряжение Ù = Uejα умножить на комплексный ток İ = Iеjβ. Однако такое произведение не имеет никакого смысла. Оно будет содержать сумму начальных фаз  +β и, следовательно, окажется зависимым от начальных фаз напряжения и тока, т. е. от момента наблюдения.
+β и, следовательно, окажется зависимым от начальных фаз напряжения и тока, т. е. от момента наблюдения.
При известных напряжении и токе в двухполюснике, заданных в комплексной форме, мощность, поступающая в двухполюсник, может быть определена на основании следующих соображений.
Пусть заданы векторы Ù = Uejα и İ = Iеjβ. Выражение активной мощности преобразуем следующим образом:
 .
.
Но UI cos ( - β) есть вещественная часть комплексного выражения
- β) есть вещественная часть комплексного выражения  .
.
Аналогично реактивную мощность

можно представить в виде мнимой части того же комплексного выражения.
Таким образом, если комплексное напряжение Ù=Uejα умножить на комплексную величину, сопряженную с комплексным выражением тока  , то вещественная часть полученного произведения будет представлять собой активную мощность, поступающую в двухполюсник, а мнимая—реактивную. (Звездочкой над
, то вещественная часть полученного произведения будет представлять собой активную мощность, поступающую в двухполюсник, а мнимая—реактивную. (Звездочкой над 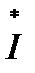 будем обозначать комплексную величину, сопряженную с комплексной величиной İ)
будем обозначать комплексную величину, сопряженную с комплексной величиной İ)
Комплексная полная мощность
 . (3.34)
. (3.34)
Если мнимая часть комплексного выражения полной мощности положительна, то двухполюсник обладает индуктивной реакцией. Если же она отрицательна, реакция двухполюсника - емкостная.
Если комплексные выражения напряжения  и тока
и тока  написаны в алгебраической форме, то комплексная полная мощность
написаны в алгебраической форме, то комплексная полная мощность
 .
.
(вещественная и мнимая части этого выражения  имеют тот же смысл активной и реактивной мощностей соответственно).
имеют тот же смысл активной и реактивной мощностей соответственно).
При работе любой электрической цепи должен иметь место баланс мощностей, иными словами, алгебраические суммы активных и реактивных мощностей, развиваемых генераторами, должны равняться, соответственно, алгебраическим суммам активных и реактивных мощностей, поступающих во все пассивные элементы цепи, включая и внутренние сопротивления генераторов.
Полная мощность, развиваемая генератором, есть произведение э.д.с. генератора, записанной в комплексной форме, на комплексную величину, сопряженную с комплексным выражением тока через генератор:
 .
.
Полная мощность, поступающая в любой пассивный элемент цепи
 ,
,
где  — напряжение на этом пассивном элементе.
— напряжение на этом пассивном элементе.
Полную мощность, поступающую во внутреннее сопротивление генератора, удобней записать в другой форме:
 .
.
Уравнение баланса мощностей
 .
.
Полная мощность, отдаваемая генератором во внешнюю цепь:
 .
.
Если активная мощность, развиваемая генератором или отдаваемая генератором во внешнюю цепь, окажется отрицательной, то данный генератор не отдает, а поглощает энергию, т. е. является приемником.
Когда в цепи работает один генератор напряжения, мощность, отдаваемая им во внешнюю цепь, будет наибольшей, если эквивалентное реактивное сопротивление внешней цепи будет равно и противоположно по знаку внутреннему реактивному сопротивлению генератора, а активные сопротивления генератора и внешней цепи равны между собой. Действительно, ток в такой цепи
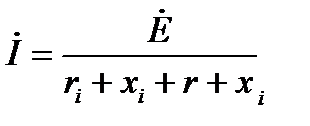 ,
,
где ri и xi - внутренние сопротивления генератора; r и х - сопротивления внешней цепи.
Ток будет максимальным при заданных активных сопротивлениях, если подобрать х = - хi. В этом режиме
 или
или 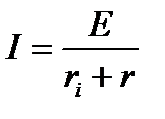 .
.
Мощность Р = I2r, расходуемая во внешней цепи, будет максимальной, если, кроме того, активное сопротивление внешней цепи подобрать равным активному сопротивлению генератора.
Таким образом, мощность, отдаваемая приемнику, максимальна, если полное сопротивление приемника и полное внутреннее сопротивление генератора — сопряженные комплексы.