Магнитосвязанные электрические цепи

 

В предыдущих главах были рассмотрены электрические цепи, в которых электромагнитная энергия из одного контура цепи в другой передавалась с помощью проводов. В электрических устройствах связи передача энергии и связь между контурами часто осуществляется путем взаимоиндукции.

Если магнитный поток, создаваемый током в одном контуре, пронизывает другой какой-либо контур, то эти два контура называют магнитосвязанными. Магнитная связь между контурами может быть специально создана, и в этом случае она полезна, а может быть и паразитной, т. е. существующей между контурами или эле­ментами цепи вопреки желанию конструктора.

1. Взаимная индуктивность. На рис. 3.44, изображены два магнитосвязанных контура. В контуре 1 протекает ток i₁. Магнитный поток Ф₁, создаваемый этим контуром, пропорционален току в контуре, так как никаких ферромагнитных материалов ни сами контуры, ни окружающая их среда не содержат. Если контур состоит из нескольких витков , то потокосцепление этого контура ψ₁, т. е. сумма магнитных потоков, сцепленных с отдельными витками контура, тоже пропорциональна току в контуре i₁.

Коэффициент пропорциональности, связывающий потокосцепление контура с создающим его током в контуре, как уже упоминалось в гл. 1, есть индуктивность контура L: ψ₁= L₁i₁.

Примем за положительное направление магнитного потока, пронизывающего контур, направление потока, связанное с направлением тока в контуре правилом буравчика. При этом условии индуктивность контура — величина положительная.

Часть магнитного потока, создаваемого током i₁, пронизывает витки второго контура. Потокосцепление со вторым контуром также пропорционально току i₁:

,

где ψ₁ — потокосцепление со вторым контуром, создаваемое током в первом контуре.

Коэффициент пропорциональности называется взаимной индуктивностью. (Условимся при обозначении величин буквой с двойным индексом второй цифрой индекса считать номер контура, создавшего эту физическую величину.)

Взаимная индуктивность представляет собой отношение потокосцепления с одним контуром к создающему его току в другом кон­туре. Один из контуров считается первым, другой - вторым. При этом совершенно безразлично, какой из контуров считать первым. Можно показать, что взаимная индуктивность, определяемая как ψ₂₁ /i₁ когда магнитный поток создается током в первом контуре, или как ψ₁₂/i₂ когда поток создается током во втором контуре и ψ₁₂ - поток сцепления с первым контуром, — есть одна и та же величина.

Определим взаимную индуктивность между двумя обмотками, намотанными равномерно на один и тот же кольцевой сердечник по всей его окружности, предполагая, что магнитный поток, создаваемый любой из обмоток, замыкается внутри сердечника. Пусть число витков первой обмотки , второй – . Площадь сечения сердечника s и средняя длина окружности сердечника l.

Тогда индуктивность первой обмотки согласно формуле (1.1)

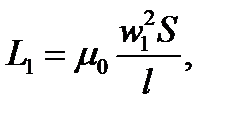
и индуктивность второй

.

Здесь μ₀ - магнитная постоянная.

Предположим далее, что в первой обмотке ток i₁ и что весь создаваемый первой обмоткой магнитный поток Ф₁ пронизывает полностью все витки и второй обмотки. Поток, создаваемый током i₁:

Ф .

Тогда потокосцепление со второй обмоткой

.

Взаимная индуктивность М между обмотками

симметрична относительно и 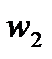, если ее определить как отношение потоков сцепления с первой обмоткой к создающему его току во второй обмотке, то выражение М осталось бы прежним.

Перемножим выражения индуктивностей обеих обмоток и сравним произведение с выражением взаимной индуктивности. Получим равенство:

.

Это равенство обязано своим существованием предположению о том, что весь магнитный поток, создаваемый первой обмоткой, полностью пронизывает и вторую. В действительности это те так, Часть магнитного потока, создаваемого обмоткой, охватывает только эту обмотку и не связана с другой (см. рис. 3.44). Эта часть магнитного потока называется потоком рассеяния. Поэтому Неравенство можно заменить равенством, введя коэффициент k, именуемый коэффициентом связи между обмотками:

или .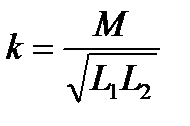

Коэффициент k всегда меньше единицы и выражается обычно в процентах.

Если бы обе обмотки были абсолютно одинаковы, коэффициент связи между обмотками представлял бы собой отношение потока, пронизывающего вторую обмотку, к потоку, создаваемому первой:

.

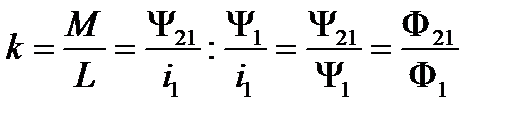Например, если считать, что каждая силовая линия на рис. 3.44 изображает некоторый определенный поток, то коэффициент связи между контурами равен 64%. Когда же L₁ ≠ L₂, коэффициент связи определяет отношение взаимной индуктивности к среднему геометрическому из индуктивностей обеих обмоток.

2. Э.д.с. взаимной индукции. Допустим, что взаимная индуктивность между контурами равна М. Если в одном из этих двух контуров ток с течением времени будет изменяться, будет изменяться и создаваемый им магнитный поток. Следовательно, магнитный поток, пронизывающий второй контур, окажется также переменным. Переменный магнитный поток, пронизывающий второй контур, вызовет в этом контуре появление индуктированной э.д.с.

Э.д.с., взаимной индукции

.

Знак «минус» в этом выражении определяет направление индуктированной э.д.с. e₂. Оно таково, что вызываемый ею ток i₂ стремится сохранить поток, пронизывающий второй контур неизменным. Так, при увеличении тока i₁ во втором контуре возник бы ток i₂ такого направления, при котором создаваемый им магнитный поток сквозь этот контур был бы направлен навстречу увеличивающемуся потоку, создаваемому током в первом контуре. Этот закон был открыт и сформулирован русским академиком Ленцем (1804—1865 гг.).

Рис.3.45. Согласное включение

Если ток в первом контуре изменяется по закону синуса: i₁=I_1msinωt, то э.д.с. e₂, индуктируемая во втором контуре, также изменяется синусоидально, отставая по фазе от тока i₁ на π/2, если положительные направления i₁ и e₂ выбраны в соответствии с выражением

.

Синусоидально изменяющиеся i₁ и e₂ можно представить в форме вещественных или мнимых частей комплексных выражений:

или .

Поэтому равенство остается справедливым и при подстановке самих комплексных выражений:

,

откуда

или .

Произведение jωM обозначается через Z_м или Z₁₂ и представляет собой сопротивление связи:

Сопротивление связи измеряется в Омах, M – в генри.

3. Согласная и встречная работа катушек. Пусть в двух магнитосвязанных катушках протекают синусоидальные токи одинаковой частоты. Создаваемые ими магнитные потоки будут также синусоидальными функциями времени. Каждая из катушек при этом пронизывается двумя магнитными потоками.

Один из них есть поток самоиндукции катушки Ф_L. Это поток, созданный током той же катушки. За положительное направление этого магнитного потока принято направление потока, создаваемого током в катушке. При этом предполагается, что направление тока в катушке совпадает с выбранным его положительным направлением.

Рис. 3.46. Встречное включение

Для того чтобы определить при этом условии направление потока, необходимо знать также и направление намотки витков катушки. На рис.3.45 указаны положительные направления токов в обмотках катушек и видны направления намотки витков. На основании этих данных легко определить положительные направления потоков самоиндукции катушек с помощью правила буравчика. Общий поток, пронизывающий первую катушку,

,

где Ф₁₂ — поток взаимоиндукции, посылаемый второй катушкой в первую.

Поток самоиндукции Ф_L1 состоит из потока взаимоиндукции, посылаемого первой катушкой во вторую Ф₂₁, и потока рассеяния первой катушки Ф_S1:

.

Аналогичное можно сказать и о второй катушке. На рис. 3.45 магнитные потоки складываются, образуя поток связи Ф_M

.

На рис. 3.46 изображены те же катушки, но направление тока во второй катушке изменено на обратное. Теперь

и

.

Здесь, как и всюду, под направлением мгновенных значений токов и потоков понимаются их положительные направления, указанные на рисунках стрелками. Следует отметить, что при определении результирующих потоков мы пользовались сложением потоков в соответствии с принципом наложения. Это оказалось возможным потому, что рассматриваемая система не содержала ферромагнитных элементов, и поэтому связь между потоками и создающими их то­ками линейна.

На рис. 3.45 поток самоиндукции каждой катушки и поток взаимной индукции, создаваемый другой катушкой, внутри катушки совпадают по направлению. В этом случае говорят, что катушки работают согласно. На рис. 3.46 потоки самоиндукции катушек и потоки взаимной индукции противоположны по направлению. Катушки работают встречно.

При изменении токов в катушках магнитные потоки, пронизывающие эти катушки, изменяются, и в катушках наводятся э.д.с.:

,

.

При согласной работе катушек э.д.с., самоиндукции и э.д.с., взаимоиндукции, наводимые в каждой из катушек, складываются, а при встречной — вычитаются.

Напряжения, возникающие на катушках, равные наводимым э.д.с., но противоположные им по направлению, при одинаковых положительных направлениях напряжений и э.д.с., будут равны:

и .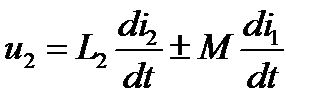

При синусоидальных токах и напряжениях эти напряжения можно записать в комплексной форме:

и .

При этом знак «плюс» между слагаемыми должен быть поставлен при согласном включении катушек, а знак «минус» — при встречном.

Если конструкция системы не известна, то определить характер (согласный или встречный) работы катушек на схеме невозможно, и автор схемы обязан снабдить изображения катушек особыми метками, которые позволили бы читателю определить характер работы катушек при выбранных читателем положительных направлениях токов. Таким образом, знание конструкции магнитопровода и направления намоток необходимо для расчета цепей с взаимной индукцией, но до выбора положительных направлений токов характер работы катушек еще не может быть определен.

4. Последовательное и параллельное соединение катушек. Предположим, что две реальные катушки, магнитосвязанные между собой, соединены последовательно и подключены к источнику синусоидального напряжения (рис. 3.47).

Напишем второе уравнение Кирхгофа для рассматриваемого контура, учитывая согласную работу катушек

.

Первое слагаемое ir₁ — падение напряжения в первой катушке благодаря ее активному сопротивлению. Второе слагаемое - падение напряжения в первой катушке, вызванное э.д.с., самоиндукции этой катушки. Третье слагаемое — падение напряжения в первой катушке, вызванное э.д.с., взаимоиндукции, созданной током второй катушки, и т. д. Перепишем уравнение для последовательного включения катушек в комплексной форме:

Рис. 3.47. Последовательное включение

Слагаемые jωMİ взяты со знаком «плюс», так как согласно маркировке при одном и том же направлении тока через катушки они работают согласно.

При встречной работе катушек уравнение имело бы такой вид:

.

Эквивалентная индуктивность последовательного соединения

L _э= L ₁+ L ₂± 2M, (3.47)

эквивалентная индуктивность каждой из катушек

L _1э = L ₁± M и L _2э = L _э ± M.

Рассмотрим подробней последние выражения для последовательного встречного включения катушек. Если бы две магнитосвязанные катушки мы решили бы заменить двумя катушками, не связанными магнитно между собой, но так, чтобы общий ток и падения напряжения на катушках оставались прежними, то индуктивности катушек следовало бы взять равными

L _1э = L ₁ – M и L _2э = L ₂ - M.

Предположим, что при одном и том же токе магнитный поток, создаваемый первой катушкой, больше, чем второй, и что, следовательно, L ₁> L ₂. Первую катушку назовем большей, а вторую — меньшей. Допустим, что катушки сблизили настолько, что взаимная индуктивность М оказалась равной индуктивности меньшей катушки М =L₂.

При этом эквивалентная индуктивность меньшей катушки равна нулю и, следовательно, равен нулю суммарный поток, пронизывающий эту катушку. При дальнейшем сближении катушек эквивалентная индуктивность меньшей катушки окажется отрицательной: М>L₂ и L₂ — М < 0.

Рис. 3.48. Параллельное включение

Напряжение на меньшей катушке будет отставать от тока по фазе как при емкостной нагрузке. Если r₁ и r₂ относительно малы, напряжение на большей катушке окажется больше напряжения, приложенного ко всей цепи. Изменение фазы напряжения на меньшей катушке при увеличении М объясняется тем, что поток взаимоиндукции, посылаемый большей катушкой в меньшую, оказался больше потока самоиндукции меньшей катушки. Фаза э.д.с., между зажимами катушки теперь определяется уже не собственным магнитным истоком, а потоком большей катушки, а при встречном включении катушек эти потоки находятся в противофазе.

Прежде чем перейти к анализу работы магнитосвязанных катушeк, соединенных параллельно, определим связь между напряжением, приложенным к катушке, и магнитным потоком, пронизывающим витки этой катушки. Для простоты анализа предположим, что активным сопротивлением катушки можно пренебречь.

Если идеальную катушку подключить к сети с синусоидальным напряжением, связь между амплитудными значениями напряжения, приложенного к катушке, и магнитного потока, ею создаваемого, определится отношением:

.

Отсюда следует, что при заданном напряжении, при заданной частоте этого напряжения и определенных витках катушки магнитный поток, пронизывающий катушку, есть величина строго определенная, не зависящая ни от каких других причин. При этом нужно отметить, что с увеличением числа витков обмотки и частоты приложенного напряжения магнитный поток, пронизывающий катушку, уменьшается, как это видно из приведенного соотношения. Объясняется это тем, что с увеличением числа витков магнитный поток должен упасть настолько, чтобы, пронизывая большее число витков, вызвать в них индуктированную э.д.с., равную приложенному напряжению. С ростом частоты скорость изменения потока увеличивается, и для создания прежней э.д.с., нужен меньший поток.

Пусть две реальные катушки, магнитносвязанные между собой, включены параллельно (рис. 3.48). Известны приложенное напряжение и параметры катушек. Требуется найти токи в ветвях и неразветвленный ток. Особенность расчета заключается в том, что несмотря на известные напряжения на катушках, раздельно определять токи в этих катушках нельзя, так как токи связаны между собой, и возможно только их совместное определение. Задачу решаем с помощью уравнений Кирхгофа:

,

,

или

,

,

здесь İ₂Z₁₂ — падение напряжения в первой катушке, создан­ное током İ₂. Знак «плюс» должен быть оставлен при согласной работе катушек, а знак «минус» — при встречном. Определяем ток İ₁:

.

Эквивалентное сопротивление первой ветви

.

Решая уравнения относительно İ₂, получим

.

Полученные выражения представляют собой эквивалентные сопротивления уже не связанных магнитно между собой ветвей, которыми можно заменить заданные магнитносвязанные ветви так, чтобы токи в ветвях остались прежними.

В выражениях Z_1Э и Z_2Э верхний знак в знаменателе получен при согласном включении катушек, а нижний — при встречном.

Так как Z_1Э и Z_2Э — сопротивления двух параллельных ветвей, уже не связанных магнитно между собой, общее эквивалентное сопротивление цепи может быть получено с помощью известной формулы

.

Для простоты анализа полученных выражений положим, что активными сопротивлениями ветвей можно пренебречь. Сократив обе части равенства на jω, сократив числитель и знаменатель правой части равенства еще раз на jω, получим

и .

Предположим, что число витков первой катушки много больше числа второй и поэтому L₁>L₂. Так как к катушкам приложено одно и то же напряжение, магнитный поток, создаваемый большей катушкой, меньше магнитного потока, создаваемого меньшей катушкой.

При встречном включении нет никаких особенностей. При согласном включении катушек следует отметить режим, при котором часть магнитного потока, создаваемого меньшей катушкой, пронизывающая большую, окажется равной тому потоку самоиндукции большей катушки, который создавала бы эта катушка при отсутствии меньшей катушки, т. е. при М = 0. Но при заданном синусоидальном напряжении магнитный поток, пронизывающий катушку, строго фиксирован и не может быть изменен. Поэтому появление в катушке потока взаимоиндукции того же направления, что и собственный поток, заставит уменьшиться поток самоиндукции, а, следовательно, и ток большей катушки. При сближении катушек поток самоиндукции исчезнет, и ток İ₁ упадет до нуля. При этом М =L₂ и L_1Э= ∞. При дальнейшем сближении катушек поток взаимо­индукции, пронизывающий большую катушку, окажется больше потока, необходимого для создания в этой катушке э.д.с., равной приложенному напряжению. Ток в обмотке большей катушки изменит фазу на 180°, и создаваемый им поток сохранит общий поток, пронизывающий эту катушку, неизменным. В этом режиме М>L₂ и L_1Э< 0. В большей катушке ток будет опережать напряжение по фазе, как в случае емкости, а не отставать от него, как это следовало бы в случае индуктивности.

Таким образом, в схемах замещения катушек, магнитносвязанных между собой, могут появиться эквивалентные отрицательные индуктивности (ложные емкости). Нельзя создать катушку с отрицательной индуктивностью, но использование в расчетах эквивалентной отрицательной индуктивности вполне допустимо.

5. Расчет сложных цепей, содержащих взаимную индуктивность. Расчет сложных цепей, содержащих магнитносвязанные катушки, можно производить с помощью уравнений Кирхгофа, учитывая при этом дополнительные напряжения, вызываемые наводимыми в катушках э.д.с., взаимоиндукций.

Методика составления уравнений не отличается от той, которой мы пользовались при расчете сложных цепей. Для уменьшения числа необходимых уравнений можно пользоваться методом контурных токов.

Однако составление контурных уравнений несколько сложнее, чем составление уравнений при непосредственном использовании уравнений Кирхгофа. Рассмотрим цепь рис. 3.49, а.

Все три катушки магнитно связаны между собой.

Сопротивления связей – x₁₂, x₂₃ и x₃₁. Конструкция магнитопровода с надетыми на него катушками неизвестна. Вместо нее на схеме указаны маркировочные метки. Выбранные направления токов показаны на рисунке. Расчет токов ветвей производим с помощью уравнений Кирхгофа. Для узла

.

Для контура x₁r₁x₃:

.

Для контура x₁r₁x₂x₄:

Рис.3.49. Расчет цепей: а – с помощью уравнений Кирхгофа б – методом контурных токов

В этих уравнениях слагаемые типа İ_kjx_nk представляют собой напряжения, создаваемые на n-й катушке током в k-й катушке. Например, — İ₁jx₃₁ есть напряжение на третьей катушке, создаваемое током впервой. Знаки подобных слагаемых зависят от харак­тера работы катушек п и k (согласного или встречного). Катушки x₃ и x₁ работают встречно, так как ток İ₁ направлен через катушку от звездочки, а ток İ₃ — через катушку х₃ направлен к звездочке. Поэтому слагаемое İ₁jx₃₁ следует писать со знаком «минус». Знак «минус» перед скобкой в последнем уравнении написан потому, что при обходе этого контура движение во второй ветви происходит против положительного направления тока İ₂.

Решим ту же задачу методом контурных токов.

Выбираем два независимых контура и положительные направления контурных токов согласно рис. 3.49,б и составляем уравнения Кирхгофа:

.

Или после приведения подобных слагаемых

.

Эти уравнения перепишем в общей форме уравнений для контурных токов

Откуда

.

Все элементы определителя можно написать для заданной цепи, не составляя предварительно уравнений Кирхгофа.

Сопротивление Z₁₁ есть собственное сопротивление первого контура. При определении этого сопротивления удобно считать, что в цепи существует только контурный ток İ₁₁, а тока İ₂₂ нет. С позиций тока İ₁₁ катушки х₁ и х₂ включены последовательно и встречно. Подобным, же образом следует составить выражение сопротивления Z₂₂.

При составлении выражения сопротивления связи между контурами необходимо учесть, что катушку х₂ следует рассматривать и как катушку, принадлежащую первому контуру, связанную согласно с катушкой x₃ второго контура, и как катушку второго контура, также связанную согласно с катушкой x₁ первого контура. Кроме того, оба контура связаны сопротивлением х₁₃ = x₃₁ и общей ветвью с –jx₂ и –jx₄.

6. Расчет мощностей. Средняя мощность, поступающая в катушку индуктивности без потерь, равна нулю. Если же катушка магнитно связана с другой катушкой, то средняя мощность, поступающая в каждую из катушек, в общем случае не равна нулю. Предположим, что цепь собрана по схеме рис. 3.48. Мощность, поступающая в одну из катушек с помощью проводов, может передаваться путем взаимной индукции в другую катушку. Первая катушка окажется потребителем энергии, и мощность, в нее поступающая, будет положительна. Вторая катушка будет играть роль генератора, так как энергию, поступающую в нее путем взаимной индукции, она будет передавать обратно в цепь с помощью проводов. Средняя мощность, поступающая во вторую катушку, окажется отрицательной. Следует отметить, что алгебраическая сумма средних мощностей всех катушек, магнитносвязанных между собой, принадлежащих цепи, равна нулю, если потерями в катушках пренебречь.

Мощность, передаваемую путем взаимной индукции, следует определять как произведение напряжения на катушке, создаваемого наведенной в ней э.д.с., взаимной индукции, на комплексное выражение, сопряженное с комплексным выражением тока через катушку. Например, средняя мощность, передаваемая путем взаимной индукции из k-и катушки в п-ю,

,

а из n-й катушки в k-ю

.

Сравнивая выражения Р_nk и P_kn можно показать, что .

Метод круговых диаграмм

1. Построение круговых диаграмм на основании векторных уравнений. Построение круговых диаграмм для разного рода схем замещения может быть проведено, если связь между напряжениями и токами, с одной стороны, и постоянными цепи, с другой, выражать через векторные уравнения и на основании таких векторных уравнений нахо­дить соответствующие геометрические места. Прежде чем применять этот метод, рассмотрим векторные уравнения простейших геометрических мест: прямой и окруж­ности.

Если

 

(3.50)

представляет собой некоторый постоянный вектор, занимающий на рисунке (рис. 3.50) определенное положение, то уравнение

 

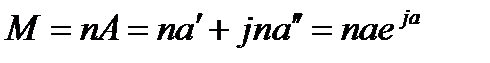(3.51)

(где n — множитель, меняющийся от — ∞ до + ∞) соответ­ствует прямой линии, проходящей через начало координат. В зависимости от значения n вектор М будет иметь ту или другую длину, но его направление остается постоянным. Уравнение

Рис. 3.50 Рис. 3.51

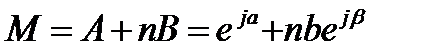(3.52)

представляет собой уравнение прямой, проведенной через конец вектора A и составляющей с осью действительных значений постоянный угол β (рис. 3.51).

При каком-нибудь значении n вектор M складывается из постоянного вектора A и переменного nВ. Таким образом, начало вектора М совпадает с точкой О, а конец лежит на прямой cd.

Уравнение

,

где A — заданный постоянный вектор, ψ — постоянный угол, а n — произвольный числовой множитель, соответствует век­торам, проходящим через начало координат, концы которых лежат на некоторой окружности. Напишем последнее уравнение в следующем виде:

(3.53)

Рис. 3.53

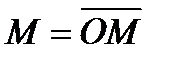При всех значениях n сумма искомого вектора и другого вектора 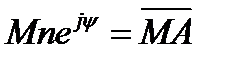, по длине в n раз большего, чем М, и составляющего с ним неизменный угол ψ, должна всегда равняться заданному вектору 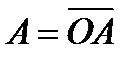. Если угол ψ положителен, то вектор 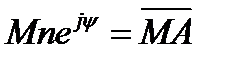должен быть повернут относительно 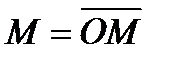против часовой стрелки (рис. 3.52). Наоборот, если угол отрицателен, то вектор 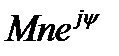поворачивается относительно 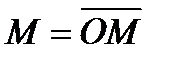по часовой стрелке (риc. 3.53).

Рис. 3.53

Рис. 3.52

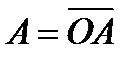Так как угол у вершины треугольника, образуемый сторонами ОМ и МА, имеет всегда одну и ту же величину π - ψ и он опирается на один и тот же отрезок ОА, то конец искомого вектора при изменении n будет перемещаться по окружности, которая может быть построена по заданному вектору и по углу ψ. Для этого мы продолжаем вектор 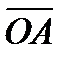и у его конца А откладываем угол ψ против стрелки часов, когда ψ положительно, и по часовой стрелке, когда ψ имеет отрицательное значение. Сторона AN угла ψ должна совпадать с направлением касательной к искомой окружности. По хорде и касательной нетрудно построить окружность.

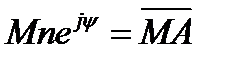Когда n=0, вектор совпадает с вектором , а будет равен нулю, т. е. точки М и A сольются, и направление вектора будет совпадать направлением касательной в точке А. По мере увеличения л конец вектора будет перемещаться по дуге АМО. При n =∞ точка M совпадает с точкой О, вектор будет равен нулю, а вектор , будет совпадать с заданным вектором .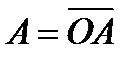

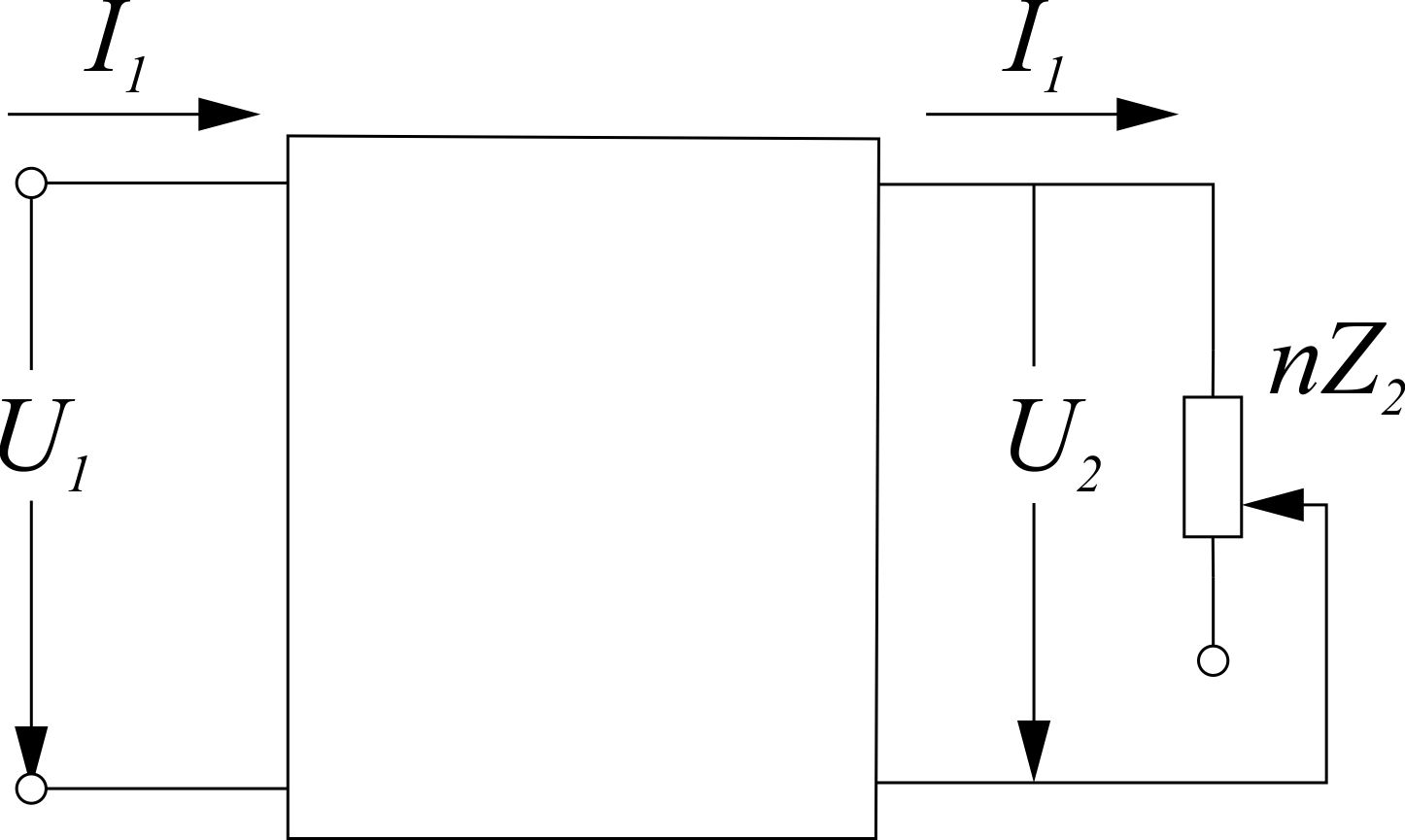Рис. 3.54

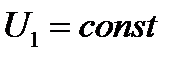Покажем, что для любого четырехполюсника при постоян­ном первичном напряжении и при однородном изменении сопротивления во вторичной цепи (cosφ₂=const) концы вектора первичного тока перемещаются по окружности независимо от того, какова внутренняя схема четырехполюсника (рис. 3.54).

При однородном из­менении сопротивления во внешней цепи отно­шение между вторичным напряжением и током может быть представлено в виде

 

 

,

где n — числовой множитель, меняющийся в пределах от 0 до ∞; очевидно, что n =0 соответствует короткому замыканию, а n =∞ холостому ходу, когда вторичная цепь разомкнута.

Если в уравнения, связывающие первичные и вторичные напряжения и токи, подставить вместо ,

,

,

и исключить к то мы получим зависимость первичного тока А от нагрузки :

; (3.54)

Когда n =∞, получим в первичной цепи ток холостого хода

;

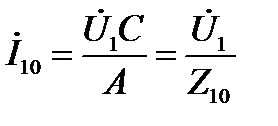Когда n =0, мы будем иметь первичный ток при том же напряжении , соответствующий короткому замыканию вторичной цепи

.

Зная токи холостого тока и короткого замыкания, мы можем определить .

Кроме того, представляет собой импеданс со стороны вторичных зажимов при кротком замыкании первичных зажимов.

Подставляя полученные выражения в уравнения для , мы находим, что

; (3.55)

Последнее уравнение представляет собой уравнение некоторой окружности, которую можно построить следующим образом (рис. 3.55): под соответствующими углами φ₁₀ и φ_1k к вектору первичного напряжения откла­дываются токи холостого хода и короткого замыкания . Соединяют концы векторов 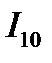и 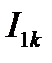линией и у конца 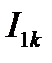этой линии под углом φ₂ - φ_2k приводят линию и затем по заданной хорде и касательной строят 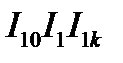окружность, которая является геометрическим местом концов вектора первичного тока.

На рис. 3.55 и 3.56 построены окружности для двух случаев: когда ток при холостом ходе отстает и когда он опережает первичное напряжение.

Рис. 3.55

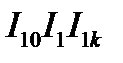При разных значениях нагрузки (но при постоянном значении cosφ₂) конец вектора первичного тока будет перемещаться по дуге от точки 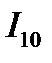, соответствующей холостому ходу, до точки 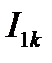, соответствующей короткому замыканию.

На тех же диаграммах мы можем отсчитать и вторичный ток I₂. Из уравнений следует:

.

Разность вектора на чертеже представляется отрезком .

,

поэтому длина отрезка , может служить мерой значения вторичного тока (но не его фазы). Если числовое значение комплекса А будет равно а, то числовое значение вторичного тока I₂ может быть выражено через

. (3.56)

Вторичное напряжение U₂ измеряется отрезком так как из построения окружности следует, что

,

 

или

,

откуда, мы получаем, ч<