Эквивалентные двухполюсники. Переходные формулы

 

Рис. 3.23. Измерение величин в двухполюснике

При заданной частоте активное и реактивное сопротивления, активная и реактивная проводимости являются параметрами двухполюсника. Для их определения опытным путем необходимо знать напряжение на двухполюснике, через него и угол сдвига между напряжением и током. Для измерения этих величин нужны вольтметр, амперметр и фазометр. Фазометр может быть заменен ваттметром. Ваттметр, включенный в цепь двухполюсника (рис. 3.23), покажет активную мощность, поглощаемую двухполюсником. 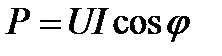Но характер (тип) реактивного сопротивления с помощью ваттметра определить нельзя, так как мощность положительна при φ>0. С помощью же фазометра определяется не только величина угла φ, но и знак этого угла. Вольтметр покажет действующее значение напряжения, а амперметр — действующее значение тока в цепи. Допустим, что измерены U, I и φ. На основании полученных данных можно построить векторную диаграмму. Однако с помощью измерительных приборов при неизменной частоте нельзя определить, содержит ли двухполюсник активное и реактивное сопротивления в последовательном или параллельном соединении.

При последовательном соединении элементов удобными параметрами цепи с точки зрения дальнейших исследований и расчетов являются полное сопротивление z, активное r и реактивное х, а при параллельном соединении полная проводимость у, активная g и реактивная b.

Рис. 3.24. Векторная диаграмма (последовательное соединение)

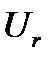Предположив, что двухполюсник состоит из последовательного соединения r и x_L, проектируем вектор напряжения на вектор тока (рис. 3.24). Проекция вектора U на вектор I_в масштабе напряжения равна напряжению на активном сопротивлении , а проекция вектора U на направление, перпендикулярное вектору I, - напряжению на индуктивности .

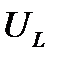Перейдем от треугольника напряжений к треугольнику сопротивлений. Параметры двухполюсника могут быть определены по следующим формулам:

, ,

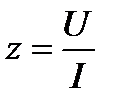; . (3.13)

Рис. 3.25. Векторная диаграмма (параллельное соединение)

Предположив теперь, что двухполюсник состоит из параллельного соединения r и x_L, спроектируем вектор тока на вектор напряжения.

Проекция вектора тока на вектор напряжения в масштабе токов будет представлять собой ток в ветви с активной проводимостью I_r, а проекция вектора I в том же масштабе на направление, перпендикулярное вектору U, — ток в ветви с реактивной проводимостью I_L (рис. 3.25). Перейдем от треугольника токов к треугольнику проводимостей. Параметры двухполюсников могут быть определены по формулам:

(3.14)

Таким образом, в зависимости от характера дальнейших расчетов можно считать двухполюсник последовательным или параллельным соединением. Заданное последовательное соединение допустимо заменить эквивалентным параллельным соединением и наоборот. Эквивалентными двухполюсниками называются такие, у которых при одинаковых напряжениях и частотах общие токи также одинаковы и по величине и по фазовому сдвигу относительно напряжения. Следовательно, для расчета двухполюсника характер соединения его элементов не играет роли. Должны быть известны его параметры r и х или g и b. Сопротивления z, r, х и проводимости у, g, b одного и того же двухполюсника или двух эквивалентных двухполюсников должны быть связаны между собой. Формулы, связывающие сопро­тивления z, r, х последовательного соединения с проводимостями у, g, b эквивалентного параллельного соединения называются переходными формулами.

Переходные формулы легко получить, сравнив между собой соотношения (3.13) и (3.14) для последовательного и параллельного соединения.

Рис. 3.26. Кривые проводимостей

­­Таким облазим, переходными формулами называют следующие равенства:

(3.15)

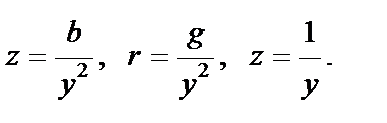(3.16)

Из переходных формул ясно, что реактивное сопротивление двухполюсника и реактивная проводимость двухполюсника—величины одного и того же знака, что в общем случае активное сопротивление двухполюсника и его активная проводимость не являются обратными величинами. То же следует сказать о реактивном сопротивлении и реактивной проводимости.

Последовательное и параллельное, соединения, эквивалентные при одной частоте питания, неэквивалентны при другой частоте.

Если ветвь содержит r и х в последовательном соединении, то при увеличении х от 0 до ∞ проводимости g, b и у этой ветви, как следует из переходных формул, будут изменяться согласно кривым рис. 3.26. Аналогичные кривые можно построить для зависимостей z, r и х от g или b.

 

 

Дуальные цепи

 

Назовем шесть уравнений, связывающих мгновенные значения напряжении и токов для трех элементов электрических цепей r, L и С, исходными уравнениями. Запишем эти уравнения в левый столбец табл. 3.1. В правый столбец табл. 3.1 перепишем эти же уравнения, предварительно заменив в них u на i, i на u, r на g, g на r, L на С, С на L. Полученные уравнения называются дуальными.

Новые уравнения оказались совпадающими с исходными, но записанными в другом порядке.

Это свойство соотношений названо двойственностью или дуальностью, а величины, взаимозаменяемые в этих уравнениях, называются дуальными. Таким образом, напряжение u и ток i — дуальные физические понятия. Дуальными пассивными элементами электрических цепей являются пары r и g, L и С.

Напишем уравнения Кирхгофа для электрической цепи, состоящей из одного контура (рис. 3.27,а):

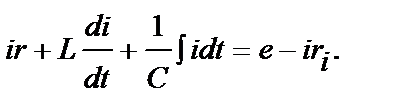
Заменим в этом уравнении все величины и элементы дуальными, считая также дуальными э.д.с., генератора напряжения и задающий ток i_o генератора тока. Получим уравнение, подобное исходному:

 

 

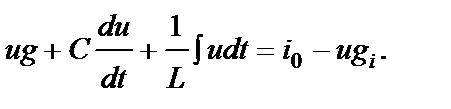
Таблица 3.1

Дуальные уравнения	Дуальные уравнения

 

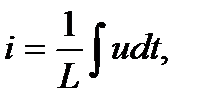
Рис. 3.27. Дуальные цепи

Это уравнение оказалось первым уравнением Кирхгофа для цепи, изображенной на рис. 3.27,б. Схемы рис. 3.27,а и 3.27,б не эквивалентны, и элементы одной из схем численно не связаны с элементами того же рода другой схемы.

Эти схемы дуальны. Обобщая определение дуальных цепей для цепей большей сложности, чем рассмотренные, будем считать дуальными цепями такие, у которых уравнения баланса напряжений для независимых контуров одной цепи при замене всех величин и элементов этой цепи дуальными преобразуются в уравнения баланса токов для независимых узлов другой цепи. В свою очередь уравнения баланса токов для независимых узлов исходной цепи при тех же заменах преобразуются в уравнения баланса напряжений для независимых контуров дуальной цепи. Исходной цепью можно считать любую из двух дуальных цепей. Из подобия уравнений Кирхгофа для дуальных цепей вытекает подобие уравнений контурных токов для исходных цепей и узловых напряжений для дуальных цепей.

Рис. 3.28. Векторные диаграммы для исходной дуальной цепи

Сравнивая обе дуальные схемы и продолжая обобщения результатов сравнения, устанавливаем, что генератор напряжения и генератор тока являются дуальными активными элементами электрических цепей. На рис. 3.27 генераторы очерчены пунктирными линиями. Последовательному соединению элементов в исходной цепи соответствует параллельное соединение дуальных элементов в дуальной цепи. Контуры и узлы дуальных цепей следует считать дуальными топологическими элементами, так как при построении дуальных схем независимые контуры исходной цепи преобразуются в независимые узлы дуальных цепей. Поэтому, общее число узлов в дуальной цепи на единицу больше числа независимых контуров исходной цепи. Число элементов, составляющих каждую из дуальных цепей, одинаково.

Из подобия уравнений для токов в исходной цепи и уравнений для напряжений в дуальной следует подобие любых зависимостей и характеристик для токов в одной и напряжений в другой из дуальных цепей. Это подобие справедливо при любых формах напряжений и токов питания в переходных и установившихся режимах работы дуальных цепей.

Очевидно, что использование свойств дуальности позволит вдвое сократить общее число исследований линейных электрических цепей. Например, исследование цепи, питаемой источником синусоидального напряжения, содержащей g и С в параллельном соединении, можно заменить исследованием цепи, с r и L, соединенными последовательно и питаемыми генератором тока. Векторные и временные диаграммы обеих цепей будут подобны, если обозначения векторов и кривых заменить на дуальные. Эти замены ясны из сравнения векторных диаграмм, построенных для исходной и дуальной цепей (рис. 3.28, а,б). Частотные характеристики токов в исходной цепи и напряжений в дуальной должны быть также подобны. Интересно отметить, что емкостный характер нагрузки исходной цепи превращается в индуктивный характер нагрузки дуальной.