Пусть вещественная функция 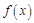 удовлетворяет условиям Дирихле на промежутке [– L, L ]. Запишем ее разложение в тригонометрический ряд Фурье:
удовлетворяет условиям Дирихле на промежутке [– L, L ]. Запишем ее разложение в тригонометрический ряд Фурье:
 , (10.1)
, (10.1)
где
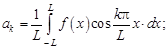
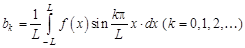 . (10.2)
. (10.2)
Если в (10.1) выразить 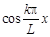 и
и  через показательную функцию от мнимого аргумента:
через показательную функцию от мнимого аргумента:


то получим ряд
 , (10.3)
, (10.3)
где в силу (10.2)
 ;
;
 ;
;
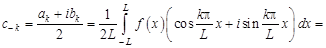
= 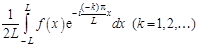
Последние три формулы можно объединить:
 . (10.4)
. (10.4)
Ряд (10.3) с коэффициентами (10.4) называется тригонометрическим рядом Фурье в комплексной форме.
Пример 1. Разложить функцию  , где
, где 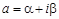 – комплексное число, в ряд Фурье на промежутке
– комплексное число, в ряд Фурье на промежутке  .
.
Решение. Найдем коэффициенты Фурье:
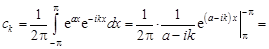
 .
.
Поскольку  , то
, то
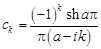 ,
, 

= 
 .
.
Искомое разложение будет иметь вид
 , (10.5)
, (10.5)
где учтено, что
 .
.
Применяя к ряду (10.5) равенство Парсеваля
 , (10.6)
, (10.6)
можно найти сумму еще одного числового ряда. Действительно, в нашем случае
 ;
;
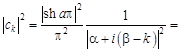
 .
.
Тогда из (10.6) следует
 .
.
Упражнение 1. Доказать, что
 ;
;  .
.
Указание. Положить в (10.5) х = 0 и х = p.
Упражнение 2. Доказать, что при 
 ;
;  .
.
Глава 2. ИНТЕГРАЛ ФУРЬЕ
Сходимость интеграла Фурье
Пусть функция  определена на всей числовой оси. Считая, что на произвольном конечном промежутке [– L, L ] заданная функция удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в комплексной форме:
определена на всей числовой оси. Считая, что на произвольном конечном промежутке [– L, L ] заданная функция удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в комплексной форме:
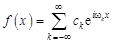 , (11.1)
, (11.1)
где
 ; (11.2)
; (11.2)
 – частота k -й гармоники;
– частота k -й гармоники; 
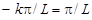 .
.
Введя в (11.1) выражения (11.2), получим
 . (11.3)
. (11.3)
При  величина
величина  . Правая часть формулы (11.3) аналогична интегральной сумме для функции
. Правая часть формулы (11.3) аналогична интегральной сумме для функции 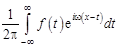 по переменной w в промежутке
по переменной w в промежутке  . Поэтому можно ожидать, что после перехода в (11.3) к пределу при
. Поэтому можно ожидать, что после перехода в (11.3) к пределу при  вместо ряда получим интеграл
вместо ряда получим интеграл
 . (11.4)
. (11.4)
Формула (11.4) называется интегральной формулой Фурье, а ее правая часть – интегралом Фурье.
Рассуждения, с помощью которых получена формула (11.4), не являются строгими и имеют лишь наводящий характер. Условия, при которых справедлива интегральная формула Фурье, устанавливает теорема, принимаемая нами без доказательства.
Теорема. Пусть функция  , во-первых, абсолютно интегрируема на промежутке
, во-первых, абсолютно интегрируема на промежутке  , т.е. интеграл
, т.е. интеграл  сходится, и, во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (– L, L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к
сходится, и, во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (– L, L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к  , т.е. равенство (11.4) выполняется при всех х из промежутка
, т.е. равенство (11.4) выполняется при всех х из промежутка  . Здесь, по-прежнему, предполагается, что в точке разрыва значение функции равно полусумме ее односторонних пределов в этой точке.
. Здесь, по-прежнему, предполагается, что в точке разрыва значение функции равно полусумме ее односторонних пределов в этой точке.
Преобразование Фурье
Интегральную формулу Фурье (11.4) преобразуем следующим образом. Положим
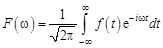 . (12.1)
. (12.1)
Если функция  непрерывна и абсолютно интегрируема на всей оси, то функция
непрерывна и абсолютно интегрируема на всей оси, то функция  непрерывна на промежутке
непрерывна на промежутке  . Действительно, так как
. Действительно, так как 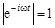 , то
, то
 , (12.2)
, (12.2)
и, поскольку интеграл справа сходится, то сходится интеграл слева. следовательно, интеграл в (12.1) сходится абсолютно. Равенство (12.2) выполняется одновременно для всех  , поэтому интеграл (12.1) сходится равномерно относительно w. Отсюда и следует, что функция
, поэтому интеграл (12.1) сходится равномерно относительно w. Отсюда и следует, что функция 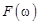 непрерывна (точно так же, как из равномерной сходимости ряда, составленного из непрерывных функций, следует непрерывность его суммы).
непрерывна (точно так же, как из равномерной сходимости ряда, составленного из непрерывных функций, следует непрерывность его суммы).
Из (11.4) получим
 . (12.3)
. (12.3)
Комплексная функция 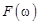 , определяемая формулой (12.1), называется преобразованием Фурье или Фурье-образом функции
, определяемая формулой (12.1), называется преобразованием Фурье или Фурье-образом функции  . В свою очередь, формула (12.3) определяет
. В свою очередь, формула (12.3) определяет  как обратное преобразование Фурье, или прообраз функции
как обратное преобразование Фурье, или прообраз функции 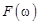 . Равенство (12.3) при заданной функции
. Равенство (12.3) при заданной функции  можно рассматривать, как интегральное уравнение относительно функции
можно рассматривать, как интегральное уравнение относительно функции 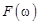 , решение которого дается формулой (12.1). И, наоборот, решение интегрального уравнения (12.1) относительно функции
, решение которого дается формулой (12.1). И, наоборот, решение интегрального уравнения (12.1) относительно функции  при заданной
при заданной 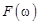 дает формула (12.3).
дает формула (12.3).
В формуле (12.3) выражение 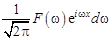 задает, условно говоря, пакет комплексных гармоник с частотами, непрерывно распределенными на промежутке
задает, условно говоря, пакет комплексных гармоник с частотами, непрерывно распределенными на промежутке 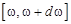 и суммарной комплексной амплитудой
и суммарной комплексной амплитудой  . Функция
. Функция 
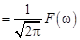 называется спектральной плотностью. Формулу (12.2), записанную в виде
называется спектральной плотностью. Формулу (12.2), записанную в виде
 ,
,
можно трактовать, как разложение функции  в сумму пакетов гармоник, частоты которых образуют сплошной спектр, распределенный на промежутке
в сумму пакетов гармоник, частоты которых образуют сплошной спектр, распределенный на промежутке  .
.
Равенства Парсеваля. Пусть  и
и 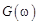 – Фурье-образы вещественных функций
– Фурье-образы вещественных функций  и
и 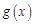 соответственно. Тогда
соответственно. Тогда
 ; (12.4)
; (12.4)
 , (12.5)
, (12.5)
т.е. скалярные произведения и нормы функций являются инвариантами преобразования Фурье. Докажем это утверждение. по определению скалярного произведения имеем 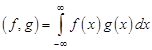 . Заменив функцию
. Заменив функцию  ее выражением (12.3) через Фурье-образ
ее выражением (12.3) через Фурье-образ  , получим
, получим
 .
.
В силу (12.1)
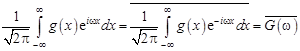 .
.
Поэтому 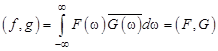 , т.е. формула (12.4) доказана. Формула (12.5) получается из (12.4) при
, т.е. формула (12.4) доказана. Формула (12.5) получается из (12.4) при  .
.
Косинус- и синус-преобразования Фурье. Если вещественная функция  четна, то ее Фурье-образ, который здесь будем обозначать
четна, то ее Фурье-образ, который здесь будем обозначать 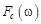 , также является вещественной четной функцией. Действительно,
, также является вещественной четной функцией. Действительно,

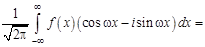
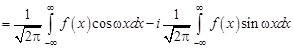 .
.
Последний интеграл, вследствие нечетности подынтегральной функции, обращается в нуль. Таким образом,
 . (12.6)
. (12.6)
Здесь использовано свойство (7.1) четных функций.
Из (12.6) следует, что функция 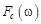 вещественна и четным образом зависит от w, так как w входит в (12.6) только через косинус.
вещественна и четным образом зависит от w, так как w входит в (12.6) только через косинус.
Формула (12.3) обратного преобразования Фурье в этом случае дает

=  .
.
Так как  и
и 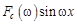 – соответственно четная и нечетная функции переменной w, то
– соответственно четная и нечетная функции переменной w, то
 . (12.7)
. (12.7)
Формулы (12.6) и (12.7) определяют косинус-преобразование Фурье.
Аналогично, если вещественная функция  нечетна, то ее преобразование Фурье
нечетна, то ее преобразование Фурье  , где
, где 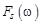 – вещественная нечетная функция от w. При этом
– вещественная нечетная функция от w. При этом
 ; (12.8)
; (12.8)
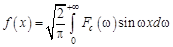 . (12.9)
. (12.9)
Равенства (12.8), (12.9) задают синус-преобразование Фурье.
Заметим, что в формулы (12.6) и (12.8) входят значения функции 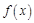 только для
только для  . Поэтому косинус- и синус-преобразования Фурье можно применять и к функции, определенной на полубесконечном промежутке
. Поэтому косинус- и синус-преобразования Фурье можно применять и к функции, определенной на полубесконечном промежутке  . В этом случае при
. В этом случае при  интегралы в формулах (12.7) и (12.9) сходятся к заданной функции, а при
интегралы в формулах (12.7) и (12.9) сходятся к заданной функции, а при  к ее четному и нечетному продолжениям соответственно.
к ее четному и нечетному продолжениям соответственно.
Покажем, как с помощью преобразования Фурье вычисляются некоторые несобственные «неберущиеся» интегралы.
Пример 1. Вычислить интеграл Лапласа 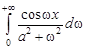 .
.
Решение. Найдем Фурье-образ функции  где
где 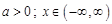 :
:



 .
.
С помощью формулы обратного преобразования Фурье

получим
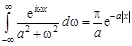
или
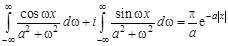 .
.
Здесь первое слагаемое представляет собой удвоенный интеграл Лапласа, а второе равно нулю вследствие нечетности подынтегральной функции. Поэтому
 .
.
Пример 2. Вычислить разрывной множитель Дирихле  , если
, если  .
.
Решение. Применив косинус-преобразование Фурье к четной функции

получим
 ;
;
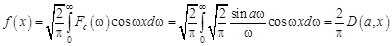 .
.
Таким образом,

В частности интеграл Дирихле
 .
.
Пример 3. Вычислить интеграл Эйлера-Пуассона  .
.
Решение. Сначала вычислим интеграл  , применив к функции
, применив к функции  , где
, где  , преобразование Фурье и введя замену
, преобразование Фурье и введя замену 

=  ;
;

 .
.
Отсюда  , и, следовательно, с заменой
, и, следовательно, с заменой 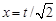 можно записать
можно записать
 .
.
Упражнение 1. Используя равенство Парсеваля, вычислить интегралы
 ;
;  .
.
Упражнение 2. Доказать, что
 ,
,
используя равенство Парсеваля.
Основные сведения