Преобразование Лапласа
Понятие оригинала. Кусочно-непрерывная функция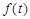 
называется оригиналом, если выполняются следующие условия:
1) 
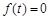для всех отрицательных t;
2) при 
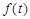растет не быстрее экспоненты, т.е. существуют такие постоянные M > 0 и c > 0, что 
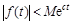для всех t.
Число с называется показателем роста 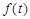. очевидно, что для ограниченных оригиналов показатель роста можно считать равным нулю.
Простейшим оригиналом является единичная функция Хевисайда
Если функция 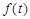удовлетворяет условию 2 и не удовлетворяет 1, то произведение 
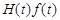будет удовлетворять и условию 1, т.е. будет оригиналом. Для упрощения записи будем, как правило, множитель H (t) опускать, считая, что все рассматриваемые в этой главе функции равны нулю при отрицательных значениях t.
Легко видеть, что оригиналами являются такие функции, как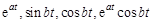 
и т.п.
Можно доказать, что сумма, разность и произведение оригиналов являются оригиналами и что оригиналом является функция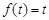 
при 
(доказательства следует найти самостоятельно).
Замечание. Из этих утверждений следует, что многочлены произвольной степени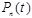 
, а также функции вида 
являются оригиналами.
Интеграл Лапласа. Интегралом Лапласа для оригинала f (t) называется несобственный интеграл вида
, (14.1)
где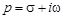 
– комплексный параметр.
Теорема. Интеграл Лапласа абсолютно сходится в полуплоскости П с: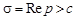 
, где с – показатель роста f (t). В самом деле, по определению оригинала имеем 
. Таким образом, интеграл (14.1) мажорируется сходящимся интегралом 
, и, следовательно, сходится абсолютно в П с.
Замечание. При доказательстве теоремы получено используемое в дальнейшем неравенство:
(14.2)
Преобразование Лапласа. Интеграл Лапласа
(14.3)
представляет собой функцию параметра p, определенную в полуплоскости П с: 
. Функция 
называется Лаплас-образом (изображением по Лапласу) оригинала 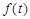. Тот факт, что 
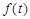есть Лаплас-образ , обозначается 
или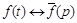 
.
Соотношение (14.3), устанавливающее связь между оригиналом и его Лаплас-образом, называется преобразованием Лапласа.
Свойства преобразования Лапласа следующие:
1. Теорема линейности. При любых постоянных 
и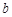 
.
Это утверждение вытекает из определения (14.3) и свойств интегралов.
2. Имеет место 
, что непосредственно следует из неравенства (14.2).
3. Теорема подобия. Для любого 
.
Действительно, полагая 
, получим
.
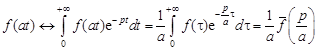4. теорема смещения. Для любого а 
. Действительно,
.
5. теорема запаздывания. Для любого 
. По определению преобразования Лапласа имеем
.
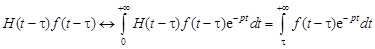Здесь учтено, что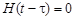 
при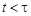 
. Выполнив в последнем интеграле замену 
, получим
.
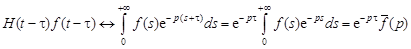Обратное преобразование Лапласа. Установим связь между преобразованиями Лапласа и Фурье. Так как при 
оригинал 
, то
где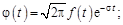 
– показатель роста 
.
Интеграл в правой части последней формулы есть интеграл Фурье для 
. Таким образом, Лаплас-образ функции является Фурье-образом функции 
. Из формулы обратного преобразования Фурье получим, что в точках непрерывности
.
Отсюда
(14.4)
Если в точке t функция терпит разрыв, то значение интеграла в (14.4) равно полусумме односторонних пределов в этой точке.
Формула (14.4) определяет обратное преобразование Лапласа, с помощью которого оригинал однозначно восстанавливается по своему изображению с точностью до значений в точках разрыва.