Свертка оригиналов. Сверткой оригиналов  и
и  называется функция
называется функция
 .
.
Функции f (t) и g (t) называются компонентами свертки.
Найдем для примера свертку произвольного оригинала  и единичной функции
и единичной функции  Имеем
Имеем  . Так как
. Так как  при
при  то
то
 . (16.1)
. (16.1)
Доказать, что свертка оригиналов – оригинал и что свертка коммутативна, т.е.  , следует самостоятельно.
, следует самостоятельно.
Теорема 1. Если  и
и  , то
, то
 .
.
Действительно, по определению (14.3) имеем

 ,
,
где D – треугольная область, задаваемая системой неравенств

Изменив порядок интегрирования в двойном интеграле, получим
 .
.
Введем вместо t новую переменную  . Тогда
. Тогда

 ,
,
что и требовалось доказать.
Пример 1. Найти оригинал  , если его Лаплас-образ
, если его Лаплас-образ  .
.
Решение. Представим данный Лаплас-образ в виде произведения двух изображений, для которых известны оригиналы:
 .
.
Так как
 ,
,
то по теореме 1 имеем

 .
.
Упражнение 1. Доказать, что свертка линейна по каждой компоненте:
 ,
,
где а и b – постоянные.
Упражнение 2. Найти свертку функций  и
и  .
.
Интегрирование и дифференцирование оригиналов. Для интегрирования и дифференцирования оригиналов справедливы следующие теоремы.
Теорема 2. Если 
 то
то  .
.
Для доказательства используем формулу (16.1) и теорему 1. Тогда
 .
.
Теорема 3. Если  и
и  – оригиналы и
– оригиналы и  , то
, то
 . (16.2)
. (16.2)
В самом деле, исходя из формулы Ньютона – Лейбница, в силу (16.1) будем иметь
 .
.
Тогда по теореме 1
 .
.
Отсюда  , что и требовалось доказать.
, что и требовалось доказать.
Применив формулу (16.2) дважды, получим


и т.д. В частности, если  , то
, то  , т.е. в этом случае дифференцирование оригинала сводится к умножению его изображения на p.
, т.е. в этом случае дифференцирование оригинала сводится к умножению его изображения на p.
Дифференцирование и интегрирование изображений. Без доказательства примем следующие свойства преобразования Лапласа:
1. Если  – оригинал с показателем роста
– оригинал с показателем роста  , то его изображение
, то его изображение  имеет в области
имеет в области  производные любых порядков.
производные любых порядков.
2. При том же условии пределы, производные и интегралы от  в области
в области 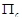 можно находить, выполняя соответствующие операции под знаком интеграла (14.3).
можно находить, выполняя соответствующие операции под знаком интеграла (14.3).
Теорема 4. Если  , то
, то  , т.е. дифференцирование изображения сводится к умножению оригинала на
, т.е. дифференцирование изображения сводится к умножению оригинала на  . Действительно, дифференцируя (14.3) по параметру p, получим
. Действительно, дифференцируя (14.3) по параметру p, получим
 .
.
Справа стоит интеграл Лапласа для функции  , следовательно,
, следовательно,
 ,
,
что и требовалось доказать.
Применив несколько раз теорему 4, получим
 .
.
Теорема 5. Если  – оригиналы и
– оригиналы и  , то
, то
 ,
,
т.е. интегрирование изображения в указанных пределах сводится к делению оригинала на  . Так как в силу (14.3) имеем
. Так как в силу (14.3) имеем  , то
, то
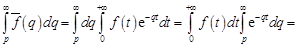
 .
.
Поскольку при  и
и  , то
, то
 .
.
Рассмотрим функции
 .
.
По теореме 4 имеем

 .
.
Так как  , то по теореме 5
, то по теореме 5
 .
.
Точно так же получим
 .
.
Применяя теорему 2, найдем изображение интегрального синуса
 .
.
Следствия из теорем 1-5 приведем с доказательствами.
Следствие 1. Если сходится интеграл
 , (16.3)
, (16.3)
то
 . (16.4)
. (16.4)
Из сходимости интеграла (16.3) следует, что изображение  непрерывно в замкнутой области
непрерывно в замкнутой области  . Переходя к пределу в (14.3) при
. Переходя к пределу в (14.3) при  , приходим к требуемому результату.
, приходим к требуемому результату.
Следствие 2. Если сходится интеграл  , то
, то
 .
.
Так как 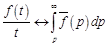 , то в силу (14.4)
, то в силу (14.4)
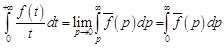 .
.
Для  справедливо равенство
справедливо равенство
 .
.
Следствие 3. Если  – оригиналы, то
– оригиналы, то  . Действительно, по теореме 3
. Действительно, по теореме 3
 . (16.5)
. (16.5)
С другой стороны,  (см. § 14). Переходя к пределу в (16.5) при
(см. § 14). Переходя к пределу в (16.5) при  , получим требуемый результат.
, получим требуемый результат.
Следствие 4. Если  – оригиналы и существует конечный предел
– оригиналы и существует конечный предел  , то
, то
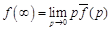 . (16.6)
. (16.6)
Исходим из равенства
 . (16.7)
. (16.7)
В силу (14.4) и теоремы 3
 . (16.8)
. (16.8)
Из (16.7) и (16.8) получаем (16.6).
Формула (16.6) позволяет исследовать поведение оригиналов при 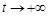 , имея в своем распоряжении только их изображения.
, имея в своем распоряжении только их изображения.
Упражнение. Вычислить несобственный интеграл  , где
, где  .
.