Господариков А.П.
Г723. Ряды Фурье. Интеграл Фурье. Операционное исчисление: Учебно-методическое пособие / А.П. Господариков, Г.А. Колтон, С.А. Хачатрян; Санкт-Петербургский государственный горный институт (технический университет). СПб, 2005. 102 с.
ISBN 5-94211-104-9
УДК 512 + 517.2 (075.80)
ББК 22.161.5
| ISBN 5-94211-104-9 | Ó Санкт-Петербургский горный институт им. Г.В.Плеханова, 2005 г. |
Введение
Из теории Фурье известно, что при некотором воздействии на физические, технические и другие системы, его результат повторяет форму начального входного сигнала, отличаясь только масштабным коэффициентом. Понятно, что на такие сигналы (их называют собственными) система реагирует наиболее простым образом. Если произвольный входной сигнал есть линейная комбинация собственных сигналов, а система линейна, то реакция системы на этот произвольный сигнал есть сумма реакций на собственные сигналы. И поэтому полную информацию о системе можно получить по «кирпичикам» – откликам системы на собственные входные сигналы. Так поступают, например, в электротехнике, когда вводят частотную характеристику системы (передаточную функцию). Для наиболее простых линейных, инвариантных во времени систем (например, описываемых обыкновенными дифференциальными уравнениями с постоянными коэффициентами) в некоторых случаях собственными функциями являются гармоники вида 
. Таким образом можно получить и результат произвольного воздействия на систему, если последний будет представлен в виде линейной комбинации гармоник (в общем случае, в виде ряда Фурье или интеграла Фурье). Вот одна из причин, по которой в теории и приложениях возникает потребность применения понятия тригонометрического ряда (ряда Фурье) или интеграла Фурье.
Глава 1. РЯДЫФУРЬЕ
Векторные пространства
Здесь приведены краткие сведения из векторной алгебры, необходимые для лучшего понимания основных положений теории рядов Фурье.
Рассмотрим множество W геометрических векторов (векторное пространство), для которого обычным образом введены понятие равенства векторов, линейные операции (сложение и вычитание векторов, умножение вектора на число) и операции скалярного умножения векторов.
Введем в пространстве W ортогональный базис, состоящий из трех попарно ортогональных векторов 
, 
и 
. Произвольный вектор 
является линейной комбинацией векторов базиса:
. (1.1)
Коэффициенты l i (i = 1, 2, 3), называемые координатами вектора 
относительно базиса 
, могут быть определены следующим образом. Скалярное произведение вектора и одного из векторов базиса 
.
В силу ортогональности базиса скалярные произведения 
при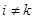 
, следовательно, в правой части последнего равенства отлично от нуля лишь одно слагаемое, соответствующее 
, поэтому 
, откуда
, (1.2)
где 
.
Если векторы 
и 
заданы своими координатами 
и 
, то их скалярное произведение
.
Так как при 
скалярное произведение , то в двойной сумме отличны от нуля лишь слагаемые с равными индексами, поэтому
. (1.3)
В частности при 
из (1.3) следует
. (1.4)
Скалярное произведение и норма функций
Обозначим символом 
множество функций, кусочно-непрерывных на промежутке [ a, b ], т.е. функций, имеющих на промежутке [ a, b ] конечное число точек разрыва первого рода и непрерывных во всех остальных точках этого промежутка.
Скалярным произведением функций 
называется число
.
Свойства скалярного произведения функций полностью совпадают со свойствами скалярного произведения векторов:
1. 
.
2. 
.
3. 
.
4. 
; 
.
Таким образом, скалярное произведение линейно зависит от своих компонентов. Это свойство называется билинейностью скалярного произведения.
Функции 
называются ортогональными 
на [ a, b ], если 
.
Нормой функции 
на промежутке[ a, b ] называется неотрицательное число 
, квадрат которого равен скалярному произведению функции 
на себя:
.
Свойства нормы функции во многом совпадают со свойствами модуля вектора:
1. 
.
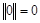2. Если функция 
непрерывна на [ a, b ] и 
, то 
. Так как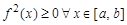 
, то при 
,
откуда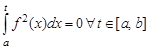 
. Дифференцируя последнее соотно- шение по 
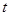и применяя теорему Барроу, получим 
и, сле-довательно, 
.
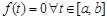3. теорема косинусов 
. 
.
Следствие. Если 
, то 
(теорема Пифагора).
4. Обобщенная теорема Пифагора. Если функции 
(k = = 1, 2, …, n) попарно ортогональны на промежутке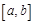 
, то
.
Используя свойство билинейности скалярного произведения, получим
.
В силу ортогональности функций 
скалярные произведения 
при 
, поэтому
.
5. неравенство Коши – Буняковского 
, или, что то же самое,
.
При любых вещественных 
.
Таким образом, квадратный трехчлен в левой части последнего не-равенства сохраняет знак на всейвещественнойоси, следовательно, его дискриминант 
.
Упражнение 1. Доказать свойства скалярного произведе-ния функций 1-3.
Упражнение 2. Показать справедливость следующих ут-верждений:
а) функция 
ортогональна функциям 
и 
на промежутке 
при любых целых k и m;
б) при любых целых k и m функции 
и 
ортогональны на промежутке 
;
в) функции и 
, а также 
и при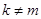 
ортогональны на промежутках 
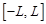и 
;
г) функции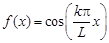 
и не ортогональны на промежутке .
Упражнение 3. Используя свойство нормы 5, доказать неравенство треугольника
.