Приближённое вычисление определённого интеграла. Формулы прямоугольников, трапеций, Симпсона

Пусть на отрезке [ a,b ] задана непрерывная положительная функция y=f(x). Требуется вычислить .

Разделим отрезок [ a,b ] точками на n равных

частей длиной . Обозначим

значения функции y=f(x) в этих точках:

(рисунок 48).

Рисунок 48

Построение интегральных сумм заключается в приближённом вычислении площади «малой трапеции» .

Существует несколько методов приближённого вычисления определённого интеграла в зависимости от способа нахождения . Рассмотрим 3 из них.

Формулы прямоугольников

Заменим каждую полученную «узкую» криволинейную трапецию прямоугольником с основанием, равным длине отрезка, на которые разбит отрезок интегрирования (= h), и высотой, равной значению функции на левом конце отрезка разбиения, т.е. , при этом (рисунок 49).

Тогда получаем формулу

(8.12)

Если при построении прямоугольников в качестве высоты рассматривать значение функции на правом конце частичных отрезков, то , тогда получаем формулу:

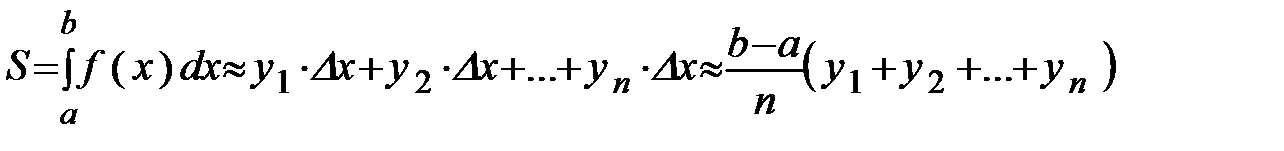(8.13)

Формулы (8.12) и (8.13) называются формулами прямоугольников.

Замечание. В случае возрастающей функции f (х) формулы прямоугольников дают приближённое значение интеграла с недостатком (8.12) и с избытком (8.13). Для убывающей функции всё наоборот.

Формула трапеций

Соединим точки и (рисунок 50) отрезком, тогда - это трапеция и её площадь равна: . Следовательно, площадь всей криволинейной трапеции приближённо равна:

(8.14)

Формула (8.11) носит название формулы трапеции.

Формула Симпсона (формула парабол)

В этом случае части кривой заменяют не прямыми линиями, как это было ранее, а дугами.

Пусть n (число делений отрезка [ a,b ]) – чётное число. На отрезке кривую заменяют параболой , проходящей через три точки , , (рисунок 51). Тогда приближённое значение интеграла вычисляется по формуле Симпсона, которая имеет вид:

. (8.15)

Рисунок 49 Рисунок 50 Рисунок 51

Пример 62. Вычислить определённый интеграл 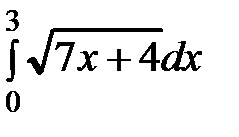по формуле Ньютона-Лейбница, а затем приближённо по формулам прямоугольников, трапеций, Симпсона, разбив отрезок интегрирования на 10 равных частей. Все вычисления производить с округлением до третьего десятичного знака. Сравнить полученные значения интеграла.

Решение. а)Вычислим интеграл по формуле Ньютона-Лейбница:

Для вычисления интеграла по приближённым формулам составим таблицу значений подынтегральной функции:

Таблица 14

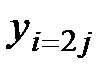
	0,3
	0,6
	0,9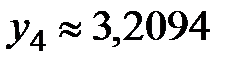
	1,2
	1,5
	1,8
	2,1
	2,4
	2,7
	3,0

б) Для удобства вычислений формулу прямоугольников (8.12) перепишем в виде: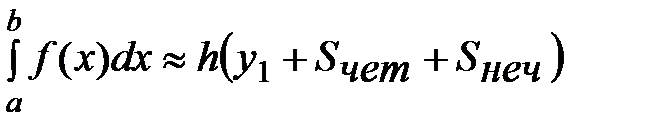

Тогда .

Так как подынтегральная функция возрастает на отрезке , то полученное приближённое значение интеграла даёт его значение с недостатком.

Абсолютная погрешность: .

Относительная погрешность: ,

Формулу прямоугольников (8.13) перепишем в виде:

.

Тогда (с избытком)

Абсолютная погрешность: .

Относительная погрешность :

в) Формулу трапеций (8.14) перепишем в виде:

.

Тогда .

Абсолютная погрешность: .

Относительная погрешность: .

г) Формулу Симпсона (8.15) запишем в виде:

.

Тогда

Абсолютная и относительная погрешности в этом случае равны 0.

Сравнивая полученные результаты, замечаем, что лучшее приближение к точному значению интеграла даёт формула Симпсона.