Пусть  - общее решение ЛОДУ,
- общее решение ЛОДУ,  - частное решение соответствующего ЛНДУ, тогда функция
- частное решение соответствующего ЛНДУ, тогда функция  является общим решением ЛНДУ.
является общим решением ЛНДУ.
1)Для нахождения общего решения ЛОДУ  составляется уравнение
составляется уравнение
 , (9.16)
, (9.16)
которое называется характеристическим. Оно получается заменой в ЛОДУ (9.14) у'' на  , y' на k, y на 1.
, y' на k, y на 1.
Уравнение (9.6), будучи квадратным уравнением, может иметь либо действительные различные корни, либо действительные равные, либо комплексные сопряженные.
Общее решение однородного уравнения зависит от вида корней характеристического уравнения.
Корни характеристического
уравнения 
| Общее решение ЛОДУ 
| |
Действительные различные корни  (D >0, D – дискриминант
характеристического уравнения) (D >0, D – дискриминант
характеристического уравнения)
| 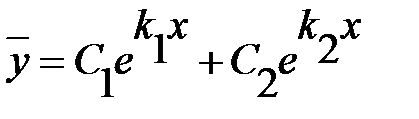
| |
Действительные равные корни  (D =0) (D =0)
| 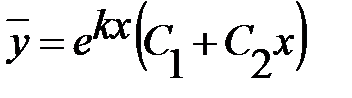
| |
Комплексные сопряженные корни  (D <0) (D <0)
|

|
Пример 74. Найти общее решение уравнения 
Решение. Составляем характеристическое уравнение, заменив у'' на  , y' на k, y на 1:
, y' на k, y на 1:  .
.
Находим его корни 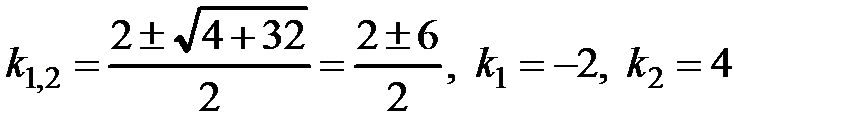 .
.
Корни характеристического уравнения действительные различные,
следовательно, общее решение имеет вид:  .
.
Пример 75. Найти общее решение уравнения: 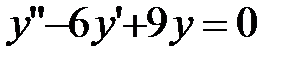 .
.
Решение. Составляем характеристическое уравнение: 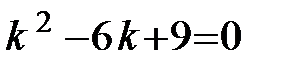 .
.
Решаем его:  .
.
 - корни характеристического уравнения действительные, равные, следовательно, общее решение имеет вид:
- корни характеристического уравнения действительные, равные, следовательно, общее решение имеет вид: 
Пример 76. Найти общее решение уравнения:  .
.
Решение. Составляем характеристическое уравнение:  .
.
Решаем его:  (
(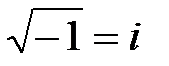 - мнимая единица, поэтому
- мнимая единица, поэтому  ).
).
 - корни характеристического уравнения комплексные сопряженные a=3, b=1, следовательно, общее решение имеет вид:
- корни характеристического уравнения комплексные сопряженные a=3, b=1, следовательно, общее решение имеет вид:
 .
.
2) Перейдем к нахождению частного решения  ЛНДУ.
ЛНДУ.
В случае, когда  - правая часть имеет специальный вид, частное решение такого уравнения может быть найдено по виду
- правая часть имеет специальный вид, частное решение такого уравнения может быть найдено по виду  методом неопределённых коэффициентов.
методом неопределённых коэффициентов.
Рассмотрим этот метод.
а) Правая часть ЛНДУ (9.13) имеет вид:  ,
,
где  - заданный многочлен степени n, a - заданное действительное число. В этом случае имеем уравнение
- заданный многочлен степени n, a - заданное действительное число. В этом случае имеем уравнение  . Его частное решение нужно искать в виде:
. Его частное решение нужно искать в виде:
 ,
,
где  - многочлен степени n с неизвестными коэффициентами, а
- многочлен степени n с неизвестными коэффициентами, а
r – кратность корня a характеристического уравнения(если a - не корень, то r= 0).
Укажем для справки общий вид многочленов нулевой, первой, второй и
третьей степеней:

Пример 77. Найти общее решение уравнения  (*).
(*).
Решение. 1) Находим сначала общее решение соответствующего однородного уравнения:  .
.
Составляем характеристическое уравнение: 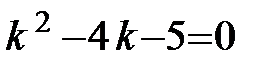 и находим его корни
и находим его корни  . Так как корни действительные и различные, то общее решение однородного уравнения имеет вид:
. Так как корни действительные и различные, то общее решение однородного уравнения имеет вид:  .
.
2) Теперь найдём частное решение  неоднородного уравнения
неоднородного уравнения  . Его правая часть
. Его правая часть  , т.е. имеет вид
, т.е. имеет вид  . Роль многочлена
. Роль многочлена  выполняет (27 х – 39) –многочлен первой степени;
выполняет (27 х – 39) –многочлен первой степени;  не совпадает ни с одним из корней характеристического уравнения, значит,
не совпадает ни с одним из корней характеристического уравнения, значит,  ищем в виде:
ищем в виде:
 . Здесь
. Здесь  - многочлен первой степени с неизвестными коэффициентами А и В, которые требуется найти. Для определения А и В дифференцируем дважды
- многочлен первой степени с неизвестными коэффициентами А и В, которые требуется найти. Для определения А и В дифференцируем дважды  :
:  ;
;
 .
.
Подставляем найденные значения в данное неоднородное уравнение:

Сократив на  , получим равенство двух многочленов:
, получим равенство двух многочленов:
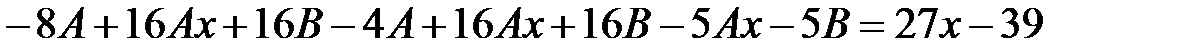 ,
,
 (**)
(**)
Известно, что два многочлена одной и той же степени равны, если они имеют равные коэффициенты при одинаковых степенях х. Приравнивая эти коэффициенты в левой и правой частях равенства (**), получим систему уравнений для определения неизвестных коэффициентов А и В.
При  ; при
; при 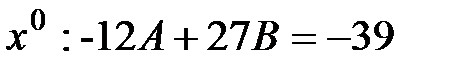 . Подставив во второе уравнение значение А, получим:
. Подставив во второе уравнение значение А, получим: 


Найдя А и В, запишем вид частного решения  :
:  . Тогда общее решение уравнения равно
. Тогда общее решение уравнения равно  .
.
Пример 78. Найти общее решение уравнения:  .
.
Решение. Общее решение данного ЛНДУ ищем в виде:  , где
, где  - общее решение соответствующего ЛОДУ;
- общее решение соответствующего ЛОДУ;  - частное решение ЛНДУ.
- частное решение ЛНДУ.
1)Выпишем соответствующее ЛОДУ:  и находим его общее решение
и находим его общее решение 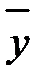 . Характеристическое уравнение:
. Характеристическое уравнение:  имеет корни
имеет корни  , следовательно,
, следовательно,  .
.
2)Находим частное решение  ЛНДУ:
ЛНДУ:  .
.
Его правая часть имеет вид: 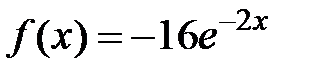 , т.е. представлена в виде произведения числа (-16), являющегося многочленом нулевой степени (
, т.е. представлена в виде произведения числа (-16), являющегося многочленом нулевой степени ( на экспоненту, у которой коэффициент
на экспоненту, у которой коэффициент  в показателе степени является двукратным корнем характеристического многочлена:
в показателе степени является двукратным корнем характеристического многочлена:  . Тогда
. Тогда  ищем в виде:
ищем в виде:  Для определения коэффициента
Для определения коэффициента  необходимо
необходимо 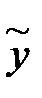 и его производные подставить в левую часть уравнения. Найдём
и его производные подставить в левую часть уравнения. Найдём 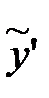 и
и  :
:

Подставим выражение для  ,
, 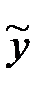 ',
',  '' в данное уравнение:
'' в данное уравнение:

Сократив обе части на  и приведя подобные, получим: 2 А = 16, А = 8. Следовательно, искомое частное решение имеет вид:
и приведя подобные, получим: 2 А = 16, А = 8. Следовательно, искомое частное решение имеет вид:  . Таким образом, общее решение данного уравнения запишется в виде:
. Таким образом, общее решение данного уравнения запишется в виде:  .
.
б) Правая часть ЛНДУ (9.13) имеет вид:  ,
,
где M, N – заданные числа.
В этом случае частное решение нужно искать в виде:
 ,
,
где А и В – неизвестные числа;
r – кратность, с которой комплексная сопряженная пара α ± i β входит в число корней характеристического уравнения.
Пример 79. Найти общее решение уравнения у '' – 2 у ' – 8 у = 17 sin3 х +6cos3 х.
Решение. Соответствующее однородное уравнение у '' + у ' – 2 у = 0. Решаем
его k2 –2 k – 8 = 0, k1 = 4, k2 = – 2.
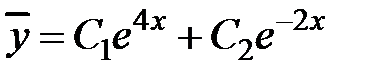 .
.
Правая часть f(х) = 8 sin2х имеет вид 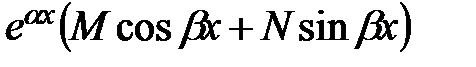 , где α = 0, β = 2, М =0, N = 8. Так как комплексная сопряженная пара α ± i β = ± 2 i не совпадает с корнями характеристического уравнения (r = 0), то частное решение имеет вид:
, где α = 0, β = 2, М =0, N = 8. Так как комплексная сопряженная пара α ± i β = ± 2 i не совпадает с корнями характеристического уравнения (r = 0), то частное решение имеет вид: 
 .
.
Дифференцируем и подставляем это решение в неоднородное уравнение:
 ;
; 



 .
.
Приравниваем коэффициенты при одинаковых тригонометрических функциях в левой и правой частях равенства:
при  :
:  ; при
; при  :
: 
Из этой системы находим А и В: 

В = –1, А = 0. Тогда частное решение равно:  , а общее решение неоднородного уравнения имеет вид:
, а общее решение неоднородного уравнения имеет вид:  .
.
Ряды
Числовые ряды
Пусть задана бесконечная последовательность чисел (действительных или комплексных)  .
.
Определение. Числовым рядом называется выражение вида
 .
.
Сокращённо ряд записывается следующим образом:  . При этом числа
. При этом числа  называются членами ряда, а число
называются членами ряда, а число  - общим членом ряда.
- общим членом ряда.
Определение. Суммы вида 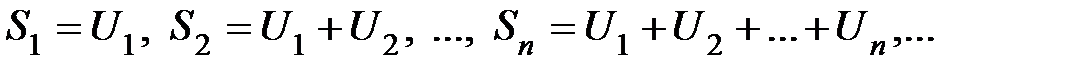 называются частичными суммами ряда.
называются частичными суммами ряда.
Ряд считается заданным, если известен закон составления каждого его члена, т.е.  .
.
Определение. Числовой ряд называется сходящимся, если существует конечный предел последовательности  его частичных сумм:
его частичных сумм:  . В этом случае число S называется суммой ряда. Если
. В этом случае число S называется суммой ряда. Если  не существует или равен бесконечности, то числовой ряд называется расходящимся и суммы не имеет.
не существует или равен бесконечности, то числовой ряд называется расходящимся и суммы не имеет.
Пример 80. Написать формулу общего члена ряда: а)  ;
;
б)  .
.
Решение. а) Если члены ряда – дроби, то для записи закономерностей их получения отдельно рассматривают числители и знаменатели. В данном примере числа 2, 5, 8, 11, …, стоящие в числителях членов ряда, образуют арифметическую прогрессию, так как каждое последующее число отличается от предыдущего на одно и то же число  , называемое разностью прогрессии. Известно, что для арифметической прогрессии
, называемое разностью прогрессии. Известно, что для арифметической прогрессии  n -ый её член может быть найден по формуле:
n -ый её член может быть найден по формуле:  , где
, где  - первый член прогрессии;
- первый член прогрессии;  - разность.
- разность.
Тогда для прогрессии 2, 5, 8, 11, …, имеем  .
.
Знаменатели членов ряда 3, 32, 33, … представляют собой геометрическую прогрессию, так как каждое последующее число получено из предыдущего путем умножения его на одно и тоже число, равное 3, которое называется знаменателем геометрической прогрессии.  Известно, что для геометрической прогрессии
Известно, что для геометрической прогрессии  её общий член
её общий член 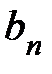 может быть найден по формуле:
может быть найден по формуле:  , где
, где  - первый член прогрессии,
- первый член прогрессии, 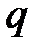 - знаменатель прогрессии.
- знаменатель прогрессии.
В нашем примере имеем  , тогда
, тогда  .
.
Следовательно, общий член ряда  записывается в виде:
записывается в виде:  .
.
б) Числители - 1, 4, 9, 16, … - квадраты последовательных натуральных чисел:  . Знаменатели можно записать так:
. Знаменатели можно записать так:  т.е.
т.е.  Указание. По определению, факториалом числа n называют произведение натуральных чисел от 1 до n, т.е.:
Указание. По определению, факториалом числа n называют произведение натуральных чисел от 1 до n, т.е.:  . При этом полагают по определению, что
. При этом полагают по определению, что  .
.
Чередование знаков у членов ряда можно получить с помощью сомножителя  . Итак,
. Итак,  .
.