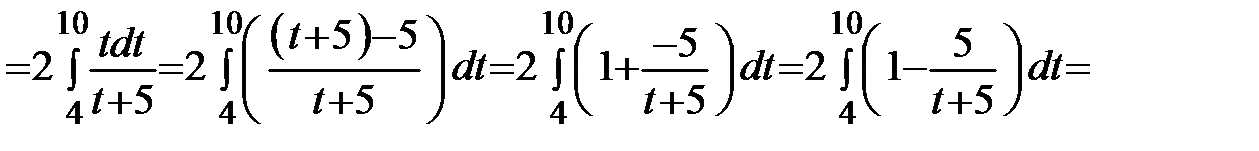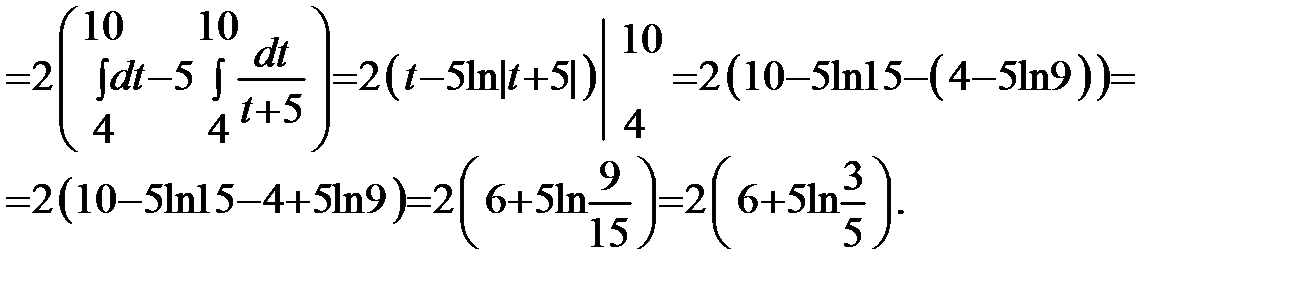Пусть функция 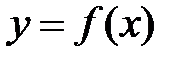 непрерывна на отрезке [ a,b ]. Выполним
непрерывна на отрезке [ a,b ]. Выполним
следующие действия: 1.Разобьём отрезок [ a,b ] на n частей точками
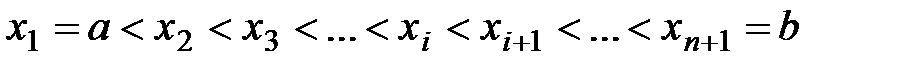 , обозначим длины отрезков:
, обозначим длины отрезков:
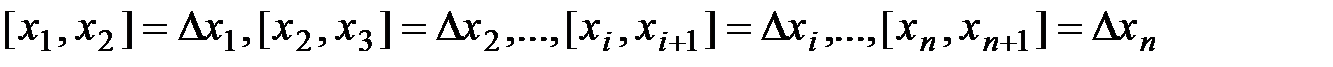 .
.
2.На каждом из этих отрезков выберем соответственно точки 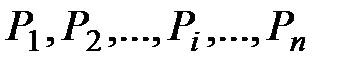 и вычислим значения функции f(x) в каждой из этих точек:
и вычислим значения функции f(x) в каждой из этих точек: 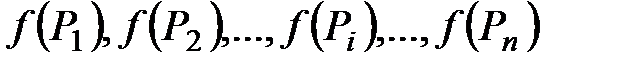 . Составим произведения:
. Составим произведения:
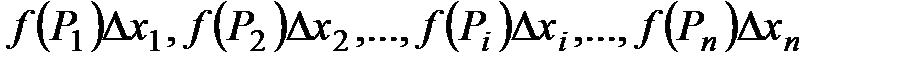 .
.
3.Составим сумму всех таких произведений и обозначим её 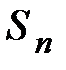 :
:
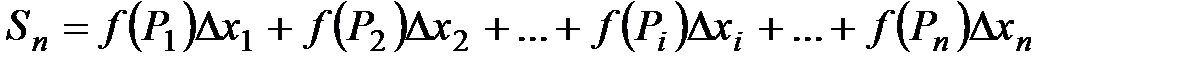 или
или 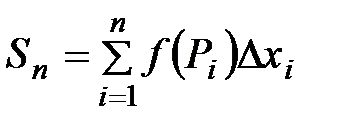
Эта сумма называется интегральной суммой для функции f(x) на отрезке [ a,b ].
4.Назовём наибольшую из длин отрезков 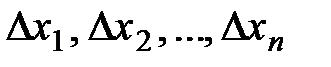 шагом разбиения и обозначим
шагом разбиения и обозначим 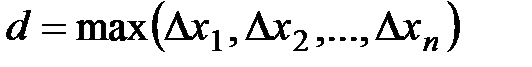 .
.
Пусть число отрезков неограниченно растёт, а шаг разбиения стремится к нулю 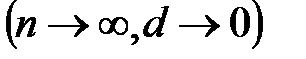 . Если при этом интегральная сумма
. Если при этом интегральная сумма 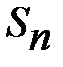 имеет предел, который не зависит ни от способа разбиения отрезка [ a,b ] на отрезки
имеет предел, который не зависит ни от способа разбиения отрезка [ a,b ] на отрезки 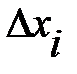 , ни от выбора точек в каждом из них, то это число называется определённым интегралом от функции f(x) на отрезке [ a,b ].
, ни от выбора точек в каждом из них, то это число называется определённым интегралом от функции f(x) на отрезке [ a,b ].
Определение. Определённым интегралом от функции f(x) на отрезке [ a,b ] называется число, равное пределу, к которому стремится интегральная сумма, когда шаг разбиения стремится к нулю, а число отрезков разбиения неограниченно растет.Обозначение: 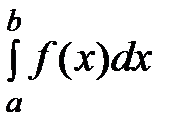 .
.
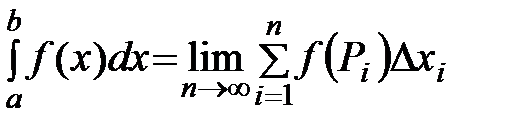 . (8.7)
. (8.7)
Числа a и b называются соответственно нижним и верхним пределамиинтегрирования. Функция f(x), для которой существует интеграл на отрезке [ a,b ], называется интегрируемой на этом отрезке.
Исходя из задачи о площади криволинейной
трапеции, можно сформулировать геометрический
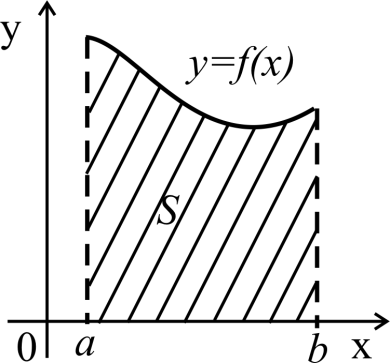 смысл определённого интеграла:
смысл определённого интеграла:
площадь криволинейной трапеции, ограниченной
сверху кривой 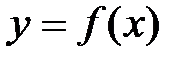
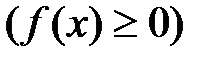 , снизу отрезком
, снизу отрезком
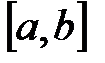 оси
оси 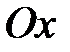 , слева и справа прямыми
, слева и справа прямыми 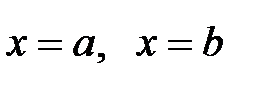 ,
,
численно равна определённому интегралу
от функции 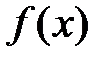 , взятому по отрезку
, взятому по отрезку 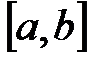
(рисунок 47). Рисунок 47
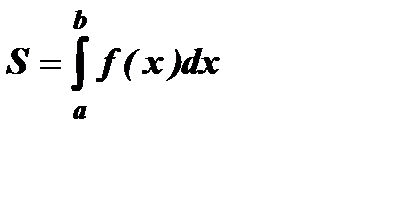 (8.8)
(8.8)
Свойства определённого интеграла. Формула Ньютона-Лейбница
1. Постоянный множитель можно вынести за знак определённого интеграла.
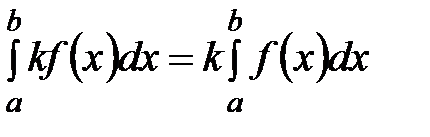 .
.
2. Определённый интеграл от алгебраической суммы нескольких функций равен алгебраической сумме определённых интегралов от этих функций.
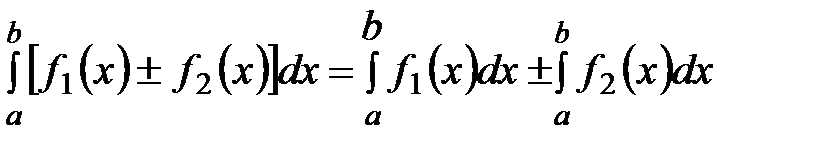 .
.
3. Если функция 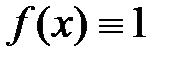 на отрезке [a,b], то интеграл от неё даёт длину этого отрезка:
на отрезке [a,b], то интеграл от неё даёт длину этого отрезка: 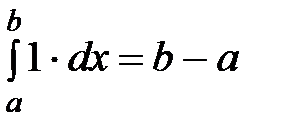 .
.
4. Если пределы интегрирования равны, то 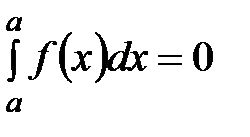 .
.
5. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный: 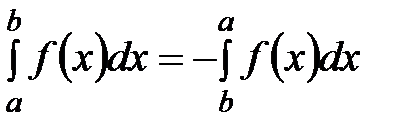 .
.
6. Свойство аддитивности определённого интеграла.
Если отрезок интегрирования [ a,b ] разбить на части [ a,c ] и [ c,b ], то:
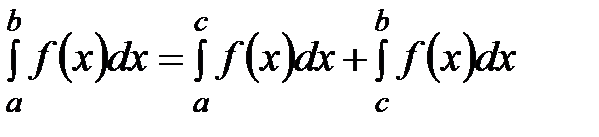 .
.
Формула Ньютона – Лейбница.
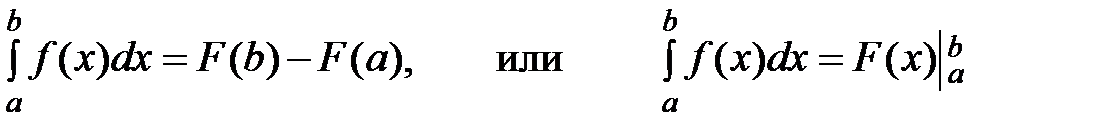 (8.9)
(8.9)
Эта формула является основной в интегральном исчислении и читается так: чтобы вычислить значение определённого интеграла, надо взять любую первообразную F(x) для функции f(x) и составить разность её значений, вычисленных при верхнем и нижнем пределах интегрирования.
Пример 57. 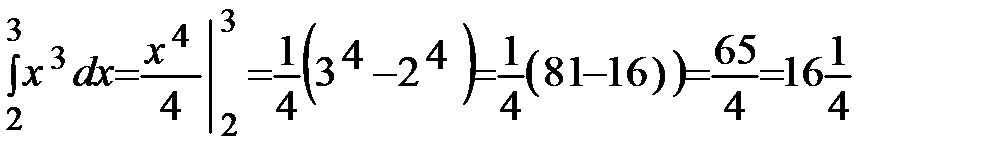 .
.
Пример 58. 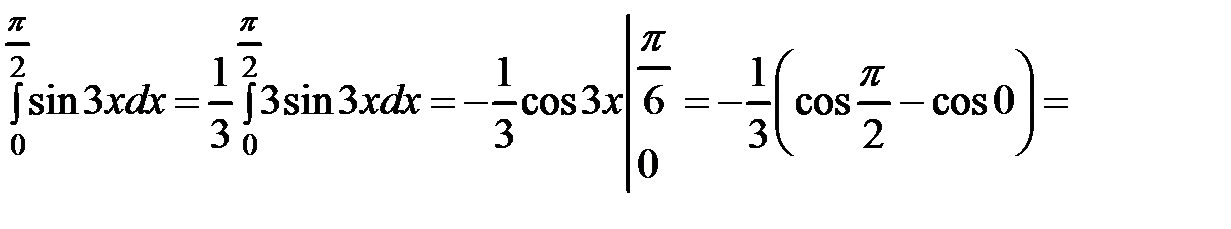 .
.
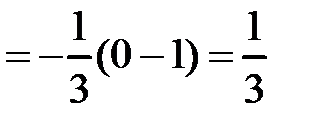 .
.
Пример 59. 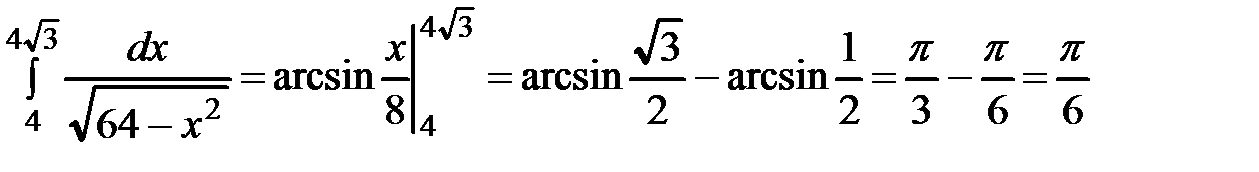 .
.
Методы интегрирования
Примеры на непосредственное интегрирование рассмотрены ранее (57, 58, 59).
Формула интегрирования по частям в определённом интеграле имеет вид: 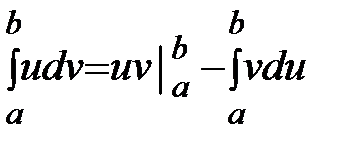 . (8.10)
. (8.10)
При применении формулы (8.10) рекомендации по выбору функций U и dV остаются теми же, что и в неопределённом интеграле.
| Þ |
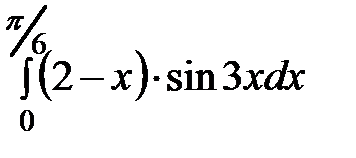
| Þ |
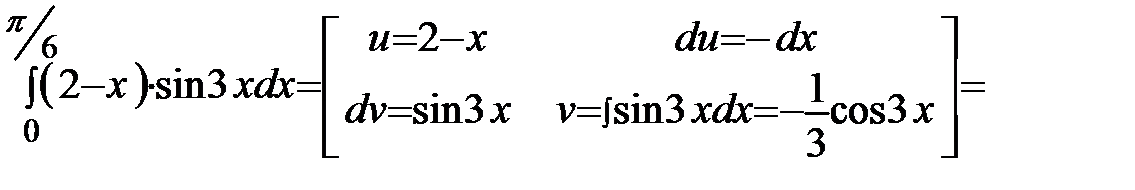
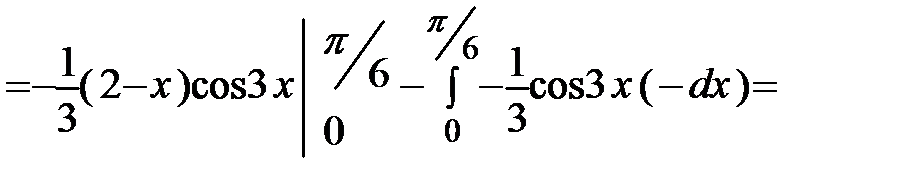
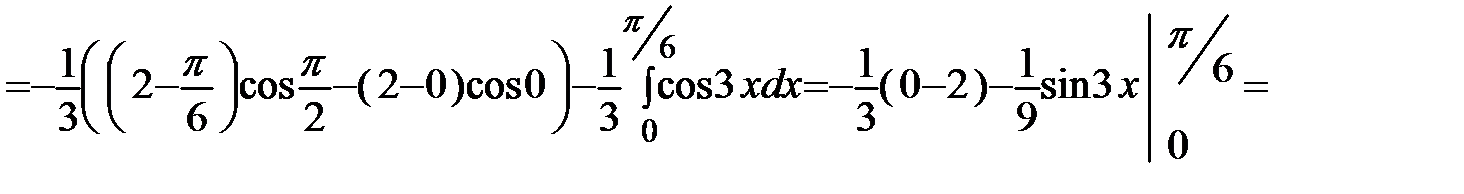
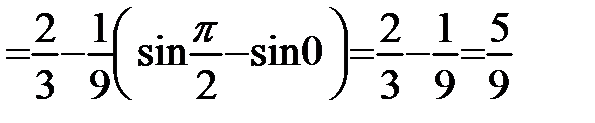 .
.
Формула замены переменной в определённом интеграле имеет вид:
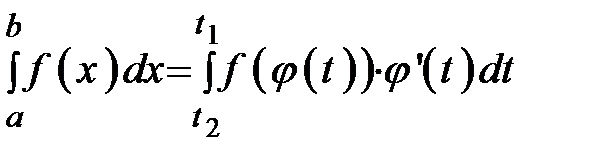 . (8.11)
. (8.11)
Следует отметить особенности формулы (по сравнению с неопределённым интегралом): 1.Необходимо находить новые пределы интегрирования 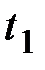 и
и 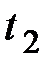 .
.
2.Не надо возвращаться к старой переменной в полученной первообразой.
3. Все рекомендации по выбору замены переменной остаются такими же, что и для неопределённого интеграла.
Пример 61. Вычислить 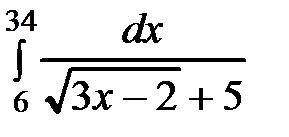 .
.
Решение. 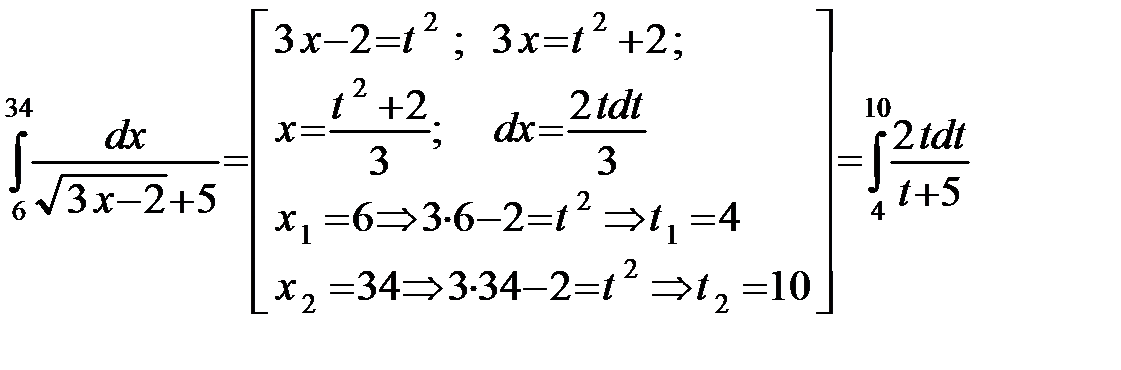 =
=