Основные правила и формулы дифференцирования
Определение. Производной функции  по аргументу
по аргументу  называется предел отношения приращения функции
называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента  при стремлении последнего к нулю (если этот предел существует).
при стремлении последнего к нулю (если этот предел существует).
 .
.
Приведём таблицу 1 правил дифференцирования и формул производных основных элементарных функций.
Пример 38. Применяя формулы и правила дифференцирования, найти
производные следующих функций: а)  ;
;
б)  ; в)
; в)  ; г)
; г)  .
.
Решение.
а) Применяя правила дифференцирования суммы (3), а так же формулы дифференцирования степенной функции (1), независимой переменной х, постояного числа получаем с, плучаем:  .
.
б) Используя правило дифференцирования произведения (4), а затем формулы дифференцирования степенной функции (1) и экспоненты (20), имеем: 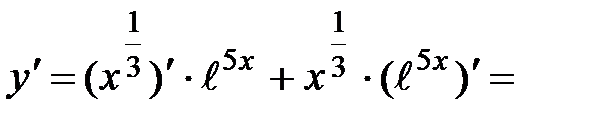


 .
.
в) Применяя правило дифференцирования частного (5), формулы дифференцирования степенной (1), логарифмической (3) функций и синуса (4), получим:



Таблица 1 – Таблица производных
Правила дифференцирования
1. 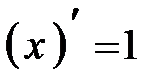 2.
2.  3.
3. 
4.  40.
40. 
5. 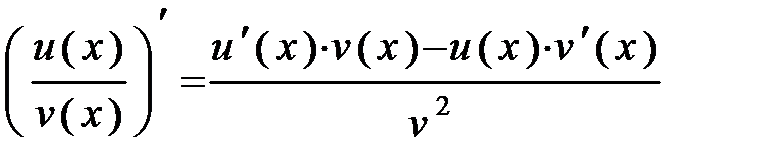 6.
6. 
60.  7.
7.  70.
70. 
Формулы дифференцирования
| Название функции | Простые функции | № п/п | Сложные функции 
|
| Степенная (n - число) | 

| 10 | 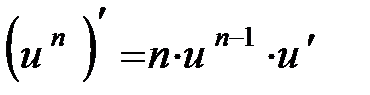
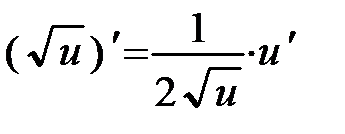
|
| Показательная (а – число) Экспонента | 

| 20 | 

|
| Логарифмическая | 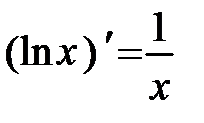

| 30 | 

|
| Тригонометрические: Синус Косинус Тангенс Котангенс |

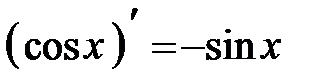


|

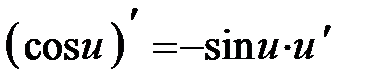


| |
| Обратные тригонометрические: | 



|
 .
.
г) 
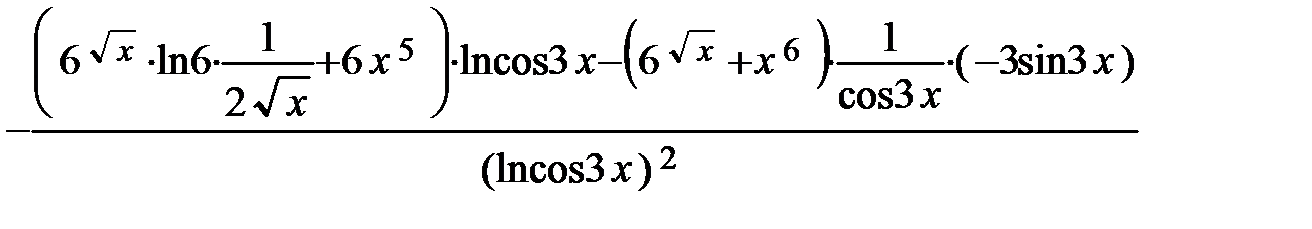
Дифференцирование неявных функций
Если функция  задана уравнением, не разрешённым относительно
задана уравнением, не разрешённым относительно 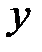 , то для нахождения производной
, то для нахождения производной  надо продифференцировать по х обе части этого уравнения, учитывая, что у есть функция от х, и затем
надо продифференцировать по х обе части этого уравнения, учитывая, что у есть функция от х, и затем
разрешить полученное уравнение относительно  .
.
Пример 39.  . Найти у ' (х).
. Найти у ' (х).
Решение. Дифференцируя по х обе части данного равенства и считая при этом у функцией от х, находим:
 или
или 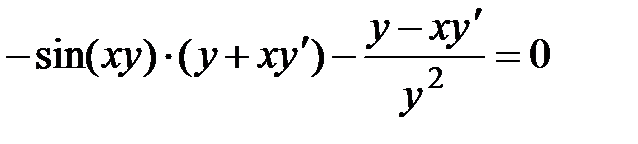 .
.
Раскроем скобки в последнем равенстве:

Разрешим полученное равенство относительно у':
 , или
, или  .
.
Дифференцирование функций, заданных параметрически
Если зависимость функции у от независимой переменной х задана с помощью вспомогательной переменной (параметра) t:
 , то
, то
 . (6.1)
. (6.1)
Пример 40. 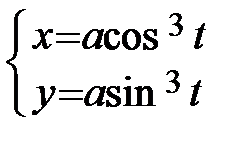 . Найти
. Найти  .
.
Решение. Дифференцируем х и у по параметру t: 
Следовательно, 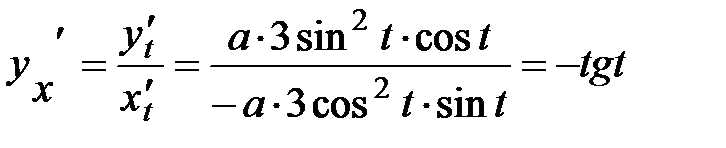 .
.
Производные высших порядков
Производная второго порядка (вторая производная) от функции
 есть производная от её первой производной:
есть производная от её первой производной:
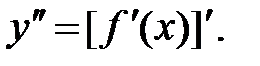 (6.2)
(6.2)
Производная третьего порядка (третья производная) от функции 
есть производная от её второй производной:
 и т. д.
и т. д.
Производная n-го порядка (n-я производная) от функции  есть
есть
производная от её (n-1)- й производной:
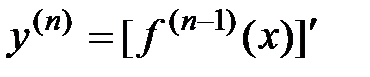 . (6.3)
. (6.3)
Пример 41. Найти значение второй производной от функции
 в точке х = 2.
в точке х = 2.
Решение. Дифференцируя данную функцию, получим:
 .
.
Дифференцируя производную  , тем самым найдём
, тем самым найдём  :
:

 .
.
При х = 2 имеем 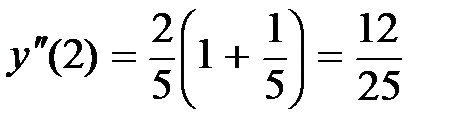 .
.
Правило Лопиталя
Основным аппаратом для раскрытия неопределённостей 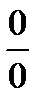 и
и 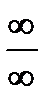
является теорема, известная под названием правила Лопиталя
Теорема Если выполнены условия:
1)  или
или 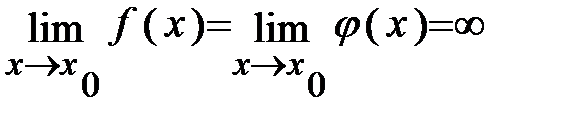 ,
,
2) функции 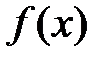 и
и  дифференцируемы в некоторой
дифференцируемы в некоторой
окрестности точки  (за исключением, быть может, её са-
(за исключением, быть может, её са-
мой), причём  ,
,
3) существует предел  , тогда
, тогда
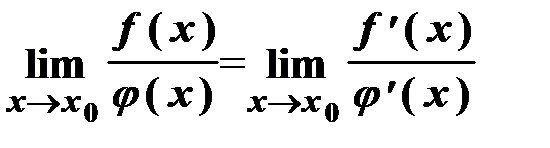 . (6.4)
. (6.4)
Это правило применимо и в том случае, когда  . Кроме того, при
. Кроме того, при
решении примера его можно применять неоднократно, если указанные выше неопределённости сохраняются.
Пример 42. Найти 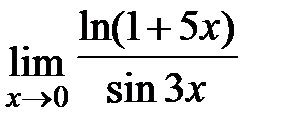 .
.
Решение. Если в заданное отношение подставить х = 0, то получим неопределённость вида  . Воспользуемся правилом Лопиталя, т. е. заменим отношение функций отношением их производных:
. Воспользуемся правилом Лопиталя, т. е. заменим отношение функций отношением их производных:
 .
.
Пример 43. Найти  .
.
Решение.  .
.
Пример 44. Найти  . Здесь имеет место неопределённость вида
. Здесь имеет место неопределённость вида  , которую раскроем, предварительно сводя её к неопределённости
, которую раскроем, предварительно сводя её к неопределённости  , а далее воспользуемся правилом Лопиталя.
, а далее воспользуемся правилом Лопиталя.
Решение. 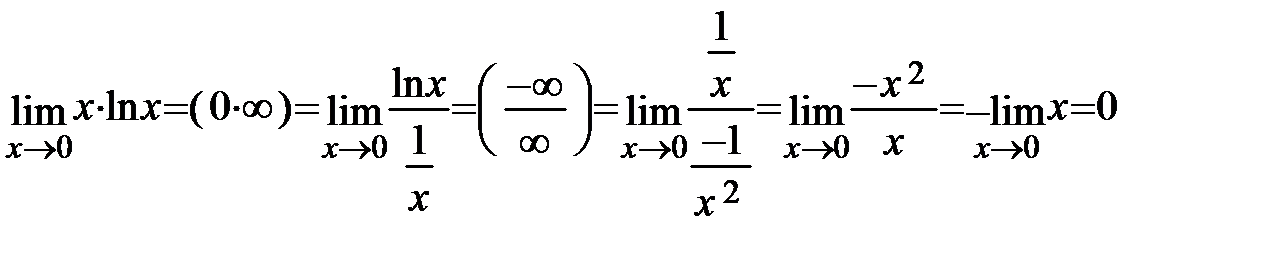 .
.