Определение. Кривая называется выпуклой (вогнутой) на интервале (а,b), если она расположена ниже (выше) касательной, проведённой к кривой в любой точке этого интервала.
Определение. Точкой перегиба называют точку, отделяющую выпуклую часть непрерывной кривой от вогнутой.
у На рисунке 36 график выпуклый на
интервале (а, х0), вогнутый – на интер-
вале (х0, b), точка Р0 – точка перегиба.
у0 Р0 Если кривая задана уравнением у = f(х),
то может быть сформулировано
следующее правило исследования на
выпуклость, вогнутость, перегиб:
1.Найти область определения функции; а х0 b х 2. Определить вторую производную у '';
Рисунок 36 3. Найти критические точки второго рода
хk (k = 1, 2, ….n) из условий: а) у '' (хk) = 0; б) у '' (хk) не существует.
4. Область определения у = f(х) разбить критическими точками второго рода на интервалы и определить знак второй производной на каждом из них. Интервалы, в которых у'' > 0, являются интервалами вогнутости кривой, а интервалы, в которых у'' < 0 - интервалами выпуклости;
5. Если при переходе через критическую точку второго рода вторая производная меняет свой знак, то эта точка – абсцисса точки перегиба;
6. Определить значение функции у = f(х) в точках перегиба.
Пример 46. Найти точки перегиба функции 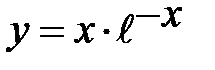
Решение. 1. Область определения функции: R = (- ¥, + ¥);
2. Находим первую и вторую производные
у' = 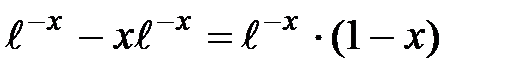 у'' =
у'' = 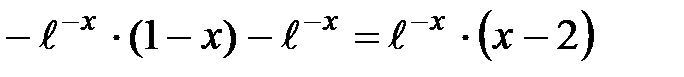
3. Находим критические точки второго рода: а) у'' = 0 Þ е – х (х – 2) = 0,
так как 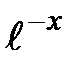 ¹ 0, то х = 2 – критическая точка второго рода:
¹ 0, то х = 2 – критическая точка второго рода:
б) у'' – существует при всех х Î R.
4. Для проверки условий существования точки перегиба мы будем пользоваться таблицей 3, подобной таблице 2, которая рассматривалась при нахождении экстремумов.
Таблица 3
| х | (-∞; 2) | (2; +∞) | ||
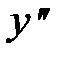
| - | + | упер = у(2) = 2 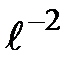
| |
| у | 2 ℓ-2 | |||
| перегиб |
Следовательно, точка 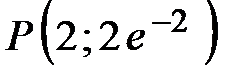 является точкой перегиба графика функции
является точкой перегиба графика функции 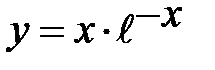 .
.
Асимптоты
Определение. Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю
при неограниченном удалении от начала координат этой
точки по кривой.
Будем различать:
- вертикальную асимптоту. Прямая х = х0 является вертикальной
асимптотой, если по крайней мере один из пределов функции
у = f(х) в точке х0 справа или слева равен бесконечности, т.е. если
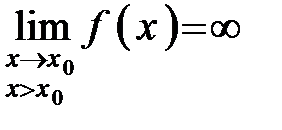 или
или 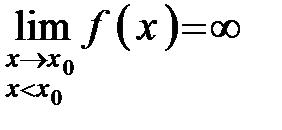 (6.5)
(6.5)
- наклонную асимптоту, имеющую уравнение у = kx + b, если существуют оба предела:
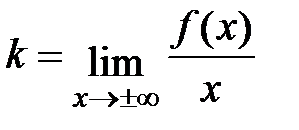 и
и 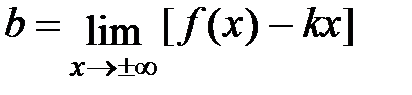 (6.6)
(6.6)
(если k= 0, то асимптота называется горизонтальной)
Пример 47. Найти асимптоты кривых: а) 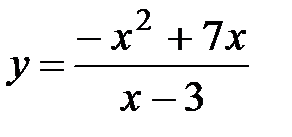 , б)
, б) 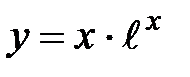 .
.
Решение. а) находим область определения функции: х – 3 ≠ 0 Þ х ≠ 3 Þ
D(у): х Î (- ¥; 3) È (3; + ¥). В точке х = 3 функция терпит разрыв.
Кривая имеет вертикальную асимптоту, которая определяется уравнением
х = 3, так как 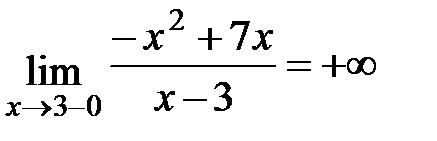 ,
, 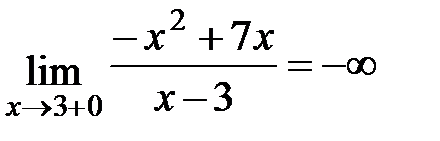 (х = 3 - точка
(х = 3 - точка
разрыва второго рода). Найдём наклонную асимптоту у = kx + b, используя для нахождения параметров k и b формулы(6.6):
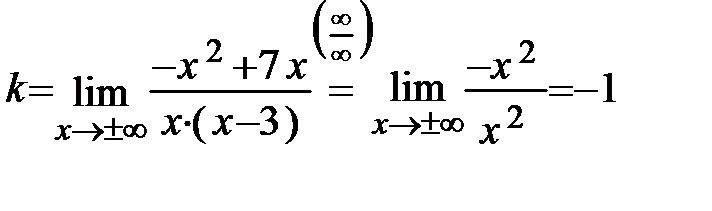 ,
, 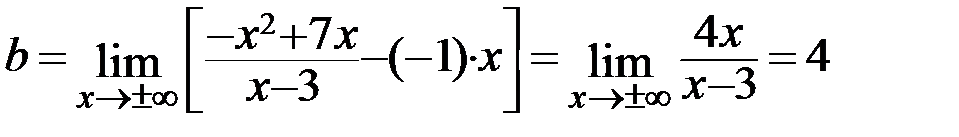 .
.
Следовательно, прямая у = - х + 4 является наклонной асимптотой графика функции 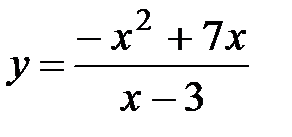 (рисунок 37).
(рисунок 37).
б) Функция 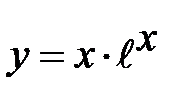 существует на всей числовой прямой, следовательно, непрерывна, вертикальных асимптот нет; наклонные асимптоты у = kx + b в данном случае нужно искать отдельно при
существует на всей числовой прямой, следовательно, непрерывна, вертикальных асимптот нет; наклонные асимптоты у = kx + b в данном случае нужно искать отдельно при 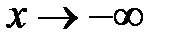 и
и  , т. к. функция
, т. к. функция 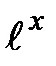 по-разному ведёт себя при
по-разному ведёт себя при 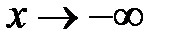 и
и 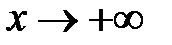 .
.
Пусть 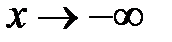 . Тогда
. Тогда 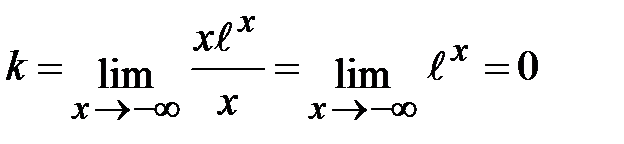
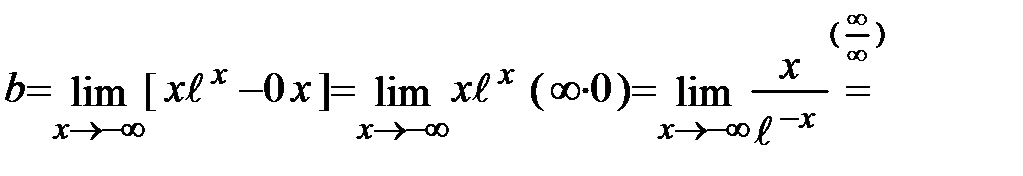
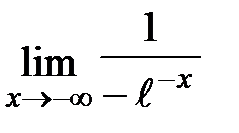 =0 (при нахождении предела использовали правило Лопиталя). Таким образом, у = 0 –наклонная (горизонтальная) асимптота при
=0 (при нахождении предела использовали правило Лопиталя). Таким образом, у = 0 –наклонная (горизонтальная) асимптота при 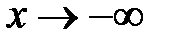 .
.
Пусть теперь 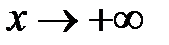 . Тогда
. Тогда 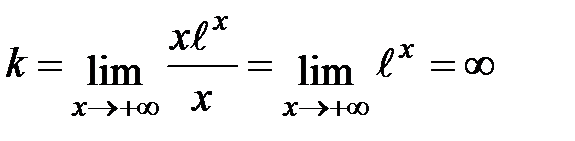 ,
,
следовательно, наклонной асимптоты при 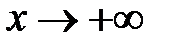 нет (рисунок 38)
нет (рисунок 38)
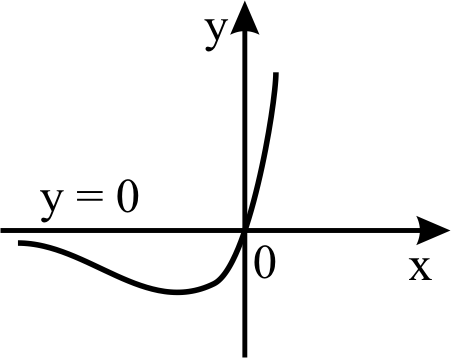
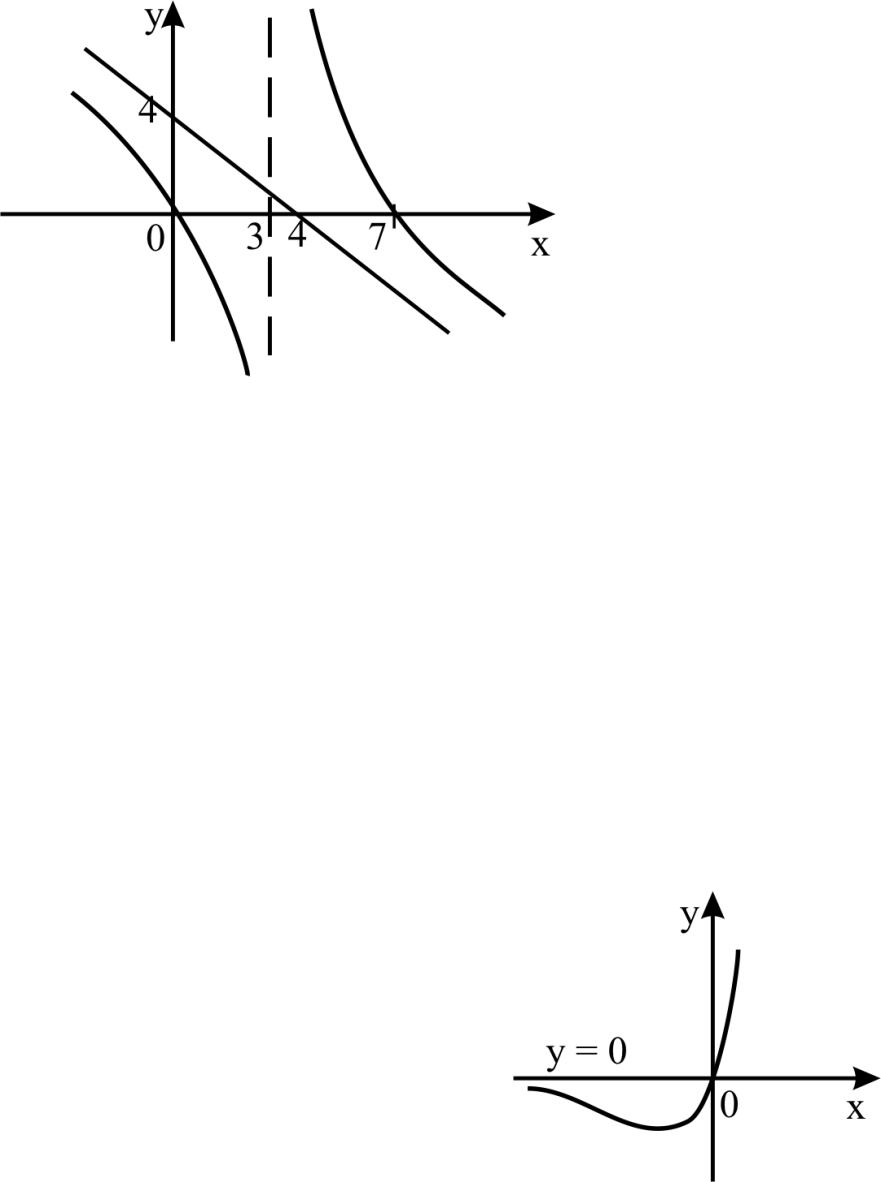
Рисунок 37 Рисунок 38
Пример 48. Исследовать функцию 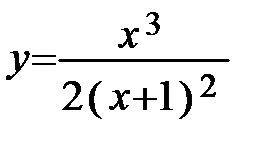 и построить её график.
и построить её график.
Примечание. Исследование функции и построение её графика можно проводить по следующей схеме:
1. Найти область определения функции
2. Исследовать функцию на непрерывность, найти точки разрыва (если они существуют)
3. Исследовать функцию на чётность и нечётность
4. Найти асимптоты графика функции
5. Найти интервалы знакопостоянства функции и точки пересечения графика функции с осями координат
6. Найти интервалы монотонности и экстремумы функции
7. Определить интервалы выпуклости, вогнутости и точки перегиба графика функции
8. На основании проведённого исследования построить график функции
| -1 |
| х |
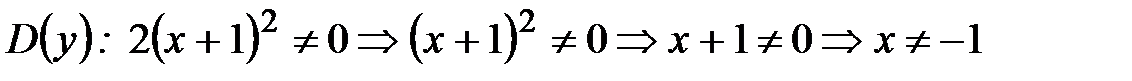 , т.е.
, т.е.
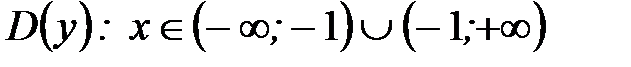 .(рисунок 39) Рисунок 39
.(рисунок 39) Рисунок 39
2. Данная функция – элементарная, поэтому непрерывна в своей области определения, т.е. на интервалах 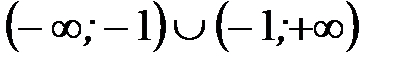 .
.
Точка 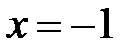 - точка разрыва. Определим характер точки разрыва. Найдём односторонние пределы функции в точке
- точка разрыва. Определим характер точки разрыва. Найдём односторонние пределы функции в точке 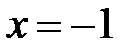 :
:
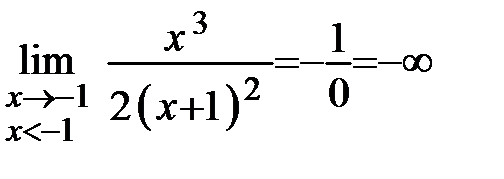 ;
; 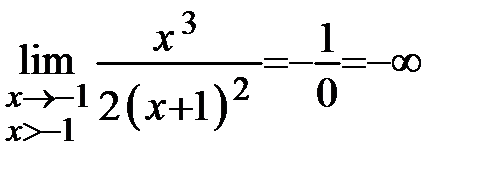 .
.
Так как односторонние пределы бесконечны, то точка 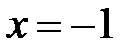 - точка разрыва второго рода.
- точка разрыва второго рода.
3. Для проверки функции на чётность и нечётность найдём: 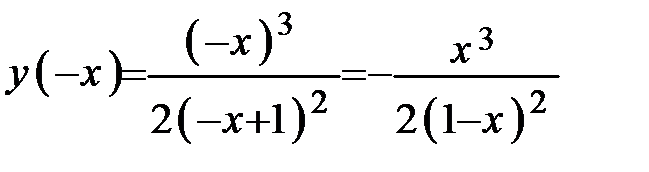 . Так как
. Так как 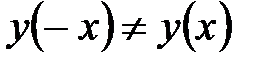 и
и 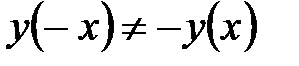 , то данная функция ни чётная, ни нечётная, то есть функция общего вида. Следовательно, график данной функции симметрией не обладает.
, то данная функция ни чётная, ни нечётная, то есть функция общего вида. Следовательно, график данной функции симметрией не обладает.
4. Определяем асимптоты графика функции. В точке 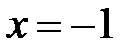 функция терпит разрыв II рода, следовательно, прямая
функция терпит разрыв II рода, следовательно, прямая 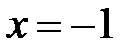 является вертикальной асимптотой. Найдём наклонные асимптоты:
является вертикальной асимптотой. Найдём наклонные асимптоты:
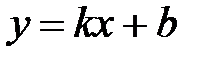 ,
, 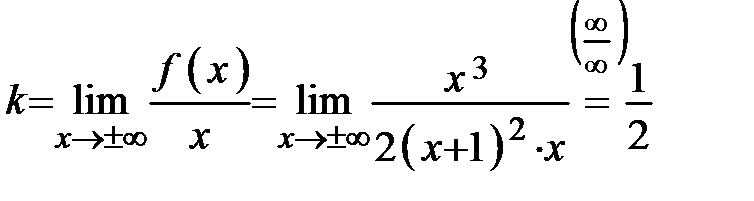 .
.
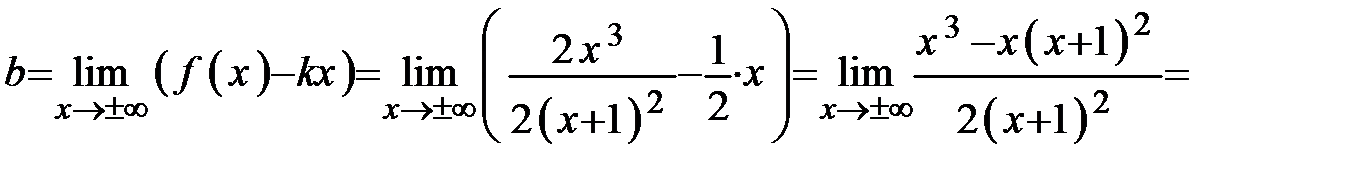
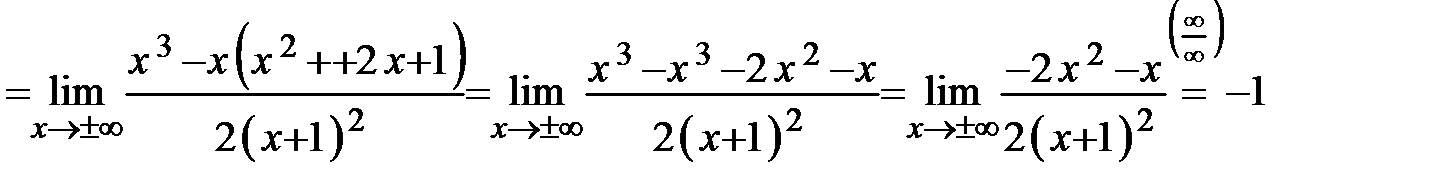 .
.
Таким образом, прямая  является Таблица 4 является Таблица 4
| |||
| наклонной асимптотой. Для её построения составим таблицу 4: | х | ||
| у | - 1 |
5. Находим интервалы знакопостоянства и точки пересечения графика функции с осями координат.
| -1 |
| х |
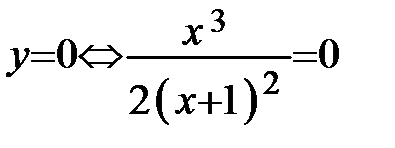 находим,
находим,
что 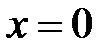 - нуль (корень) функции. Рисунок 40
- нуль (корень) функции. Рисунок 40
Полученной точкой разбиваем область определения функции на интервалы (рисунок 40) 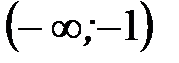 ,
, 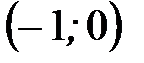 ,
, 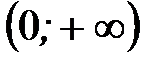 и определяем знак функции на каждом из них.
и определяем знак функции на каждом из них.
Результаты исследования занесем в таблицу 5.
Таблица 5
| х | 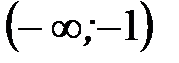
| 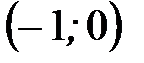
| 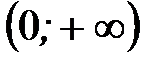
| |
| у | - | - | + | |
| график | ниже оси Ох | ниже оси Ох | точка перес. с Ох | выше оси Ох |
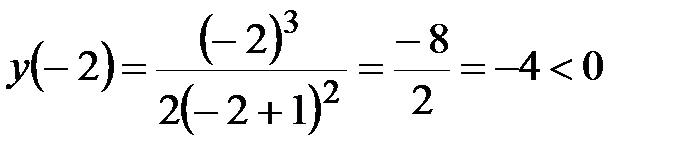
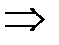 на интервале
на интервале 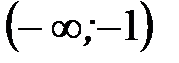 график функции лежит ниже оси Ох.
график функции лежит ниже оси Ох.
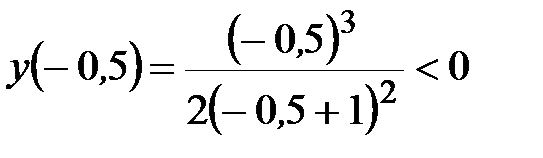 , следовательно, на интервале
, следовательно, на интервале 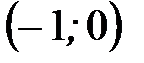 график функции также лежит ниже оси Ох.
график функции также лежит ниже оси Ох.
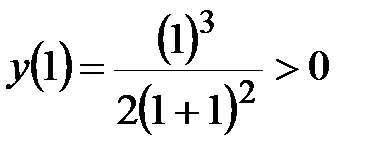 , следовательно, на интервале
, следовательно, на интервале 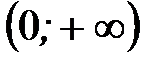 график функции лежит выше оси Ох. Так как функция меняет свой знак при переходе через точку х = 0, то эта точка является точкой пересечения графика с осью Ох.
график функции лежит выше оси Ох. Так как функция меняет свой знак при переходе через точку х = 0, то эта точка является точкой пересечения графика с осью Ох.
Находим точку пересечения графика функции с осью Оу.
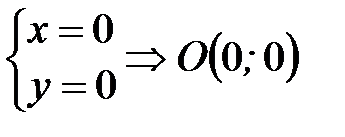 - точка пересечения графика функции с осью Оу.
- точка пересечения графика функции с осью Оу.
6. Находим интервалы монотонности и экстремумы функции.
Определяем первую производную:
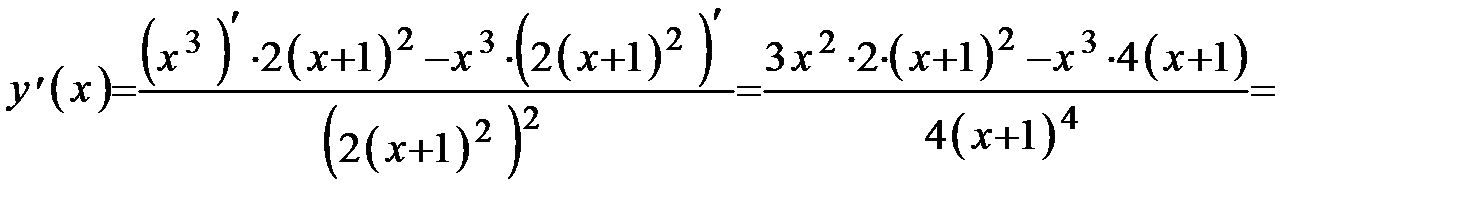
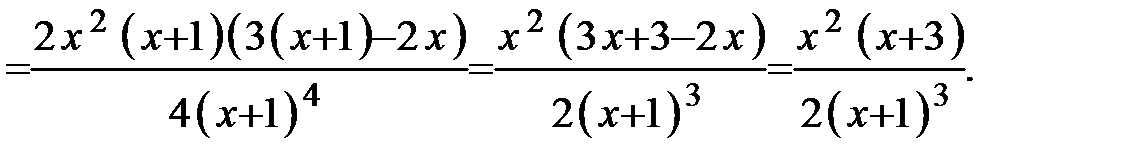
Находим критические точки I рода из условий: 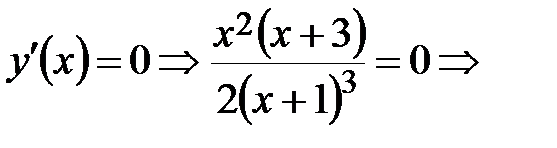
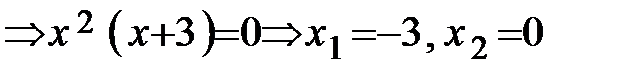 - критические точки I рода, которые входят в D(у).
- критические точки I рода, которые входят в D(у).
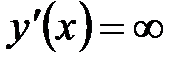 при
при 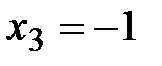 , но
, но 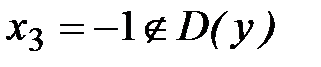 и, следовательно, критической точкой не является.
и, следовательно, критической точкой не является.
Область определения функции разбиваем найденными критическими точками на интервалы (рисунок 41) 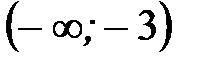 ,
, 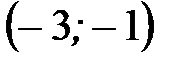 ,
, 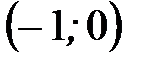 ,
, 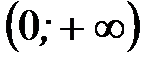
| -1 |
| х |
| -3 |
на каждом из них.
Результаты заносим в таблицу 6. Рисунок 41
Таблица 6
| х | 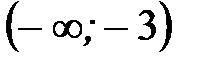
| - 3 | 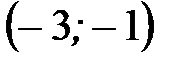
| 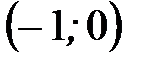
| 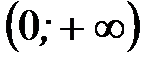
| |
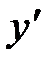
| + | - | + | + | ||
| у | 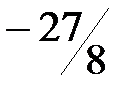
| экстр. нет | ||||
| max |
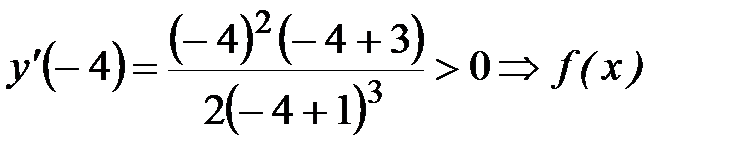 возрастает на
возрастает на 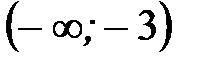 .
.
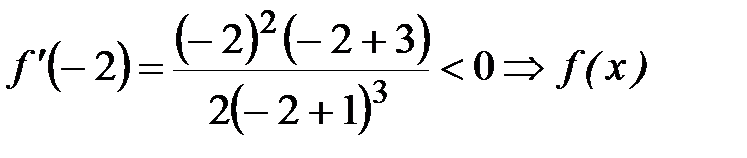 убывает на
убывает на 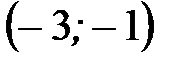 .
.
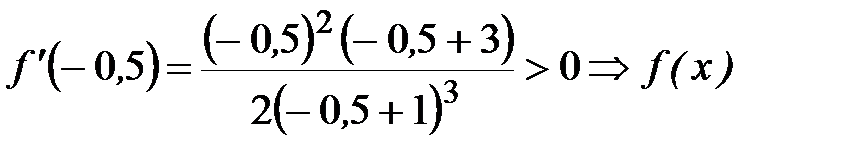 возрастает на
возрастает на 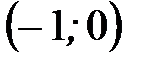 .
.
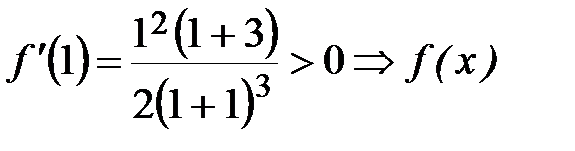 возрастает на
возрастает на 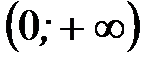 .
.
Таким образом, согласно достаточному признаку существования экстремума, в точке 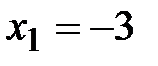 имеем максимум, а в точке
имеем максимум, а в точке 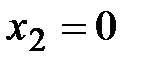 экстремума нет. Найдём
экстремума нет. Найдём 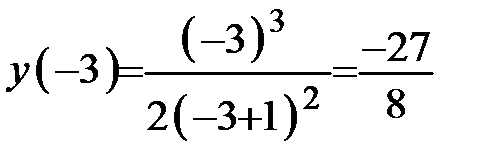 . Получаем
. Получаем 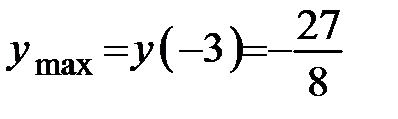 .
.
7. Определим интервалы выпуклости и вогнутости кривой и точки перегиба. Находим вторую производную: 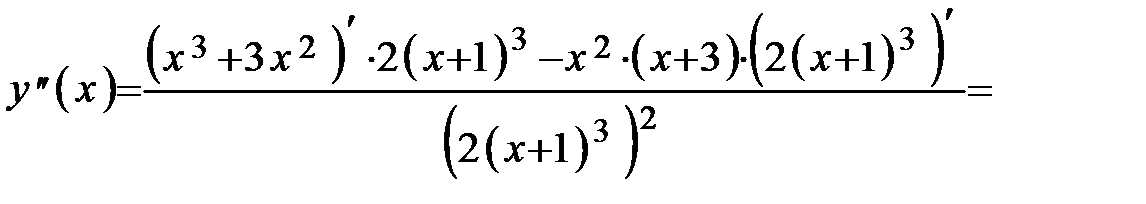
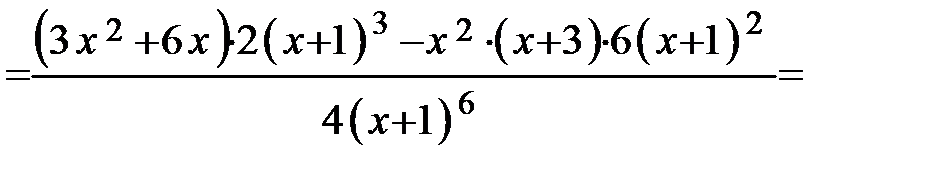
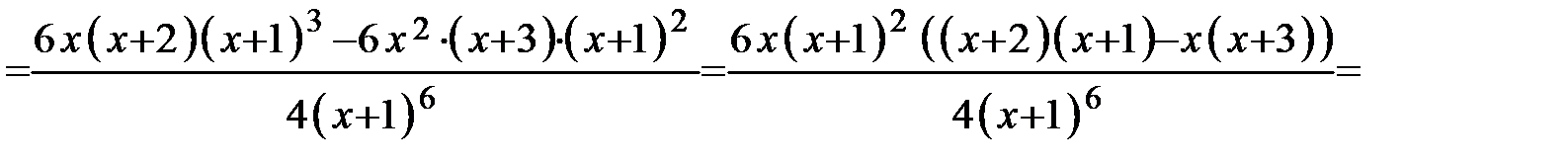
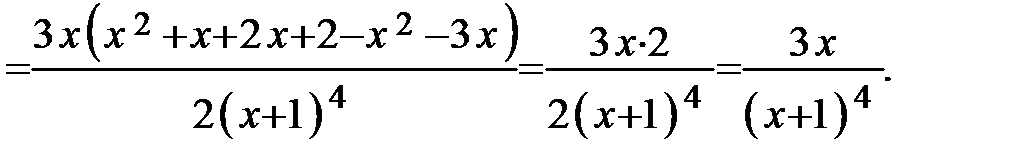
Определяем критические точки II рода из условий: 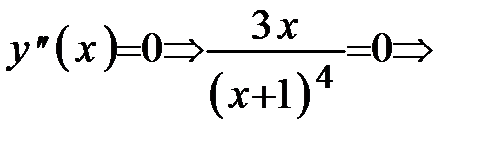
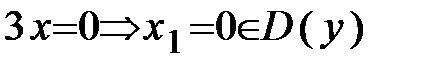 .
.

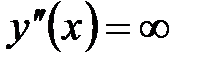 при
при  , но
, но 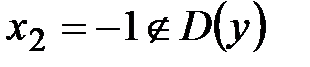 . Следовательно,
. Следовательно, 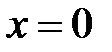 - критическая точка II рода. Полученной критической точкой разбиваем область определения функции на интервалы (рисунок 42)
- критическая точка II рода. Полученной критической точкой разбиваем область определения функции на интервалы (рисунок 42)
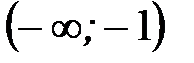 ,
, 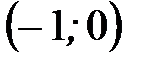 ,
, 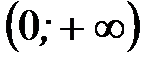 .
.
Исследуем знак второй производной на
каждом из интервалов: Рисунок 42
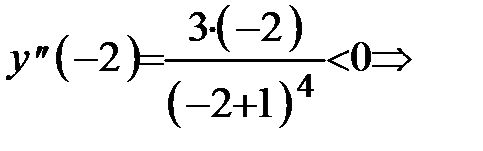 график функции на интервале
график функции на интервале 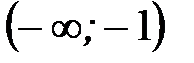 выпуклый.
выпуклый.
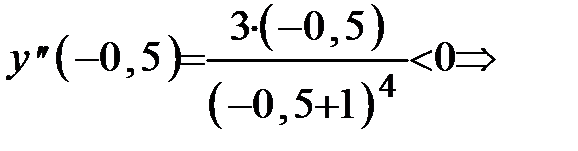 график функции на интервале
график функции на интервале 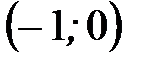 выпуклый.
выпуклый.
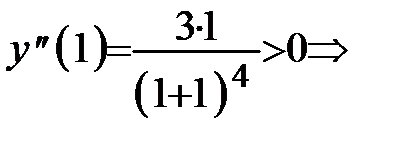 график функции на интервале
график функции на интервале 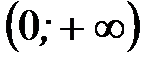 вогнутый.
вогнутый.
Результаты занесём в таблицу 7.
Таблица 7
| х | 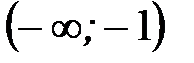
| 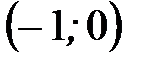
| 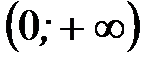
| |
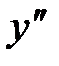
| - | - | + | |
| у | Ç | Ç | È | |
| перегиб |
Таким образом, в силу достаточного признака существования точки перегиба, точка 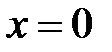 является абсциссой точки перегиба.
является абсциссой точки перегиба.
Найдём 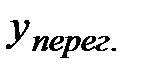 :
: 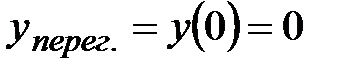 и точка
и точка 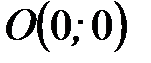 - точка перегиба.
- точка перегиба.
8. Для построения графика функции все вычисления сведем в таблицу 8. которая объединяет результаты исследований, занесённые в таблицы 8, 9, 10, 11.
Таблица 8
| х | 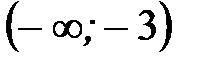
| - 3 | 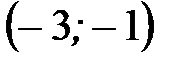
| 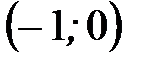
| 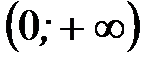
| |
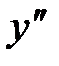
| - | - | - | + | ||
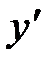
| + | - | + | + | ||
| у | - | 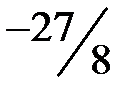
| - | - | + | |
| график | ниже Ох | max | ниже Ох | ниже Ох | т. О перегиб, пересеч. | выше Ох |
Используя результаты исследования в п.п. 1- 8, строим график (рисунок 43).
| -1 |
| -3 |
| М |
| у |
| х |
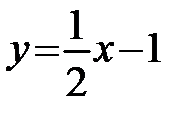
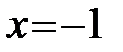
Рисунок 43