Плоскость
Если в пространстве взята прямоугольная декартова система координат, то всякое уравнение первой степени относительно текущих координат х, у и z
 , (4.1)
, (4.1)
где А, В и С одновременно не равны нулю, определяет плоскость в этой системе координат. Числа А, В, С являются координатами вектора  , перпендикулярного к плоскости. Вектор
, перпендикулярного к плоскости. Вектор 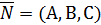 называется вектором нормали.
называется вектором нормали.
Справедливо и обратное утверждение: в пространственной прямоугольной декартовой системе координат всякая плоскость может быть представлена уравнением вида (4.1).
Уравнение (4.1) называется общим уравнением плоскости.
Отметим, что если в уравнении (4.1) отсутствует:
1) свободный член D, то плоскость проходит через начало координат;
2) одна из переменных, то плоскость параллельна той оси, название которой не входит в это уравнение. Например,  - уравнение плоскости, параллельной оси Оz.
- уравнение плоскости, параллельной оси Оz.
3) две из трёх переменных, то плоскость параллельна координатной плоскости, в название которой входят отсутствующие в уравнении переменные. Так,  - уравнение плоскости, параллельной координатной плоскости хОz.
- уравнение плоскости, параллельной координатной плоскости хОz.
4) одна из переменных и свободный член, то плоскость проходит через ось, название переменной которой отсутствует в уравнении.
Например,  - уравнение плоскости, проходящей через ось Оу.
- уравнение плоскости, проходящей через ось Оу.
 5) уравнения х =0, у =0, z =0 определяют соответственно координатые плоскости уОz, хОz, хОу.
5) уравнения х =0, у =0, z =0 определяют соответственно координатые плоскости уОz, хОz, хОу.
Уравнение плоскости, проходящей через
точку  и перпендикулярной
и перпендикулярной
вектору 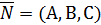 (рисунок 21) имеет вид:
(рисунок 21) имеет вид:
Рисунок 21
 . (4.2)
. (4.2)
Вектор  называется нормальным вектором плоскости.
называется нормальным вектором плоскости.
 Пусть в прямоугольной декартовой системе
Пусть в прямоугольной декартовой системе
координат (рисунок 22) заданы три точки
 ,
, 
и  .
.
Тогда уравнение плоскости, проходящей через
три данные точки имеет вид: Рисунок 22
 . (4.3)
. (4.3)
Пусть плоскости Q1 и Q2 заданы уравнениями Q1: А1х + В1у + С1z + D1 = 0,
| j |
| j |
| N |
| Q |
| Q |
| N |
Тогда углом между плоскостями Q1 и Q2
называют угол φ (рисунок 23) между нормаль-
ными векторами этих плоскостей. Нормаль-
ный вектор плоскости может иметь любое из двух
противоположных направлений, поэтому угол между
плоскостями определен неоднозначно и для него воз-
можны два значения φ и π – φ. Рисунок 23
Так как cos (π – φ) = - cos φ, то угол между плоскостями можно найти по формуле:
 (4.4)
(4.4)
| Q |
| Q |
| N |
| N |
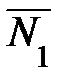 и
и 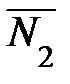 коллинеарны (рисунок 24).
коллинеарны (рисунок 24).
Условие параллельности плоскостей:
 (4.5)
(4.5)
Рисунок 24
Условие перпендикулярности двух плоскостей имеет вид
 . (4.6)
. (4.6)
Расстояние от точки  до плоскости
до плоскости  находится по формуле
находится по формуле
 . (4.7)
. (4.7)
Прямая в пространстве
Положение прямой l в пространстве вполне определяется заданием точки М0(х0; у0; z0) Î l и вектора  =(m; n; p), который параллелен этой прямой. Такой вектор
=(m; n; p), который параллелен этой прямой. Такой вектор  называется направляющим вектором прямой.
называется направляющим вектором прямой.
Пусть в пространстве в прямоугольной системе координат задана точка
М0(х0; у0; z0) є l и вектор  =(m; n; p) || l.
=(m; n; p) || l.
| x |
| y |
| S |
| z |
| M |
| l |
| M |
Пусть М(х; у; z) – текущая точка прямой l,
тогда  =(х-х0; у-у0; z-z0). Очевидно,
=(х-х0; у-у0; z-z0). Очевидно,
что вектор  коллинеарен вектору
коллинеарен вектору 
(рисунок 25). Исходя из условия коллинеарности
двух векторов, имеем канонические уравнения Рисунок 25
прямойв пространстве:  . (4.8)
. (4.8)
От канонических уравнений прямой, вводя параметр t, перейдём к параметрическим уравнениям прямой
 или
или  (4.9)
(4.9)
 Уравнения (4.9) называются параметрическими уравнениями прямой, проходящей через точку М0(х0; у0 ; z0) и имеющей
Уравнения (4.9) называются параметрическими уравнениями прямой, проходящей через точку М0(х0; у0 ; z0) и имеющей
направляющий вектор  =(m; n; p).
=(m; n; p).
Пусть заданы две точки: М1(х1; у1; z1) и
М2(х2; у2; z2). Получим уравнение прямой,
проходящей через эти точки.
Пусть М(х; у; z) – произвольная точка прямой l. Рисунок 26
 = (х - х1; у – у1; z – z1),
= (х - х1; у – у1; z – z1),  = (х2 – х1; у2 – у1; z2 – z1);
= (х2 – х1; у2 – у1; z2 – z1);
 є l,
є l,  є l,
є l,  ||
||  (рисунок 26)
(рисунок 26)
Исходя из условия коллинеарности двух векторов, имеем уравнения прямой в пространстве, проходящей через две данные точки:
 (4.10)
(4.10)
Прямая в пространстве может быть задана как линия пересечения двух плоскостей (рисунок 27). Если плоскости Q1 и Q2 заданы своими уравнениями Q1: А1х + В1у + С1z + D1 = 0, Q2: А2х + В2у + С2z + D2 = 0, то система уравнений определяет прямую в пространстве, если нормальные векторы
 =(А1; В1; С1) и
=(А1; В1; С1) и 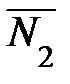 =(А2; В2; С2) неколлинеарны.
=(А2; В2; С2) неколлинеарны.
| l |
| Q |
| Q |
| N |
| N |
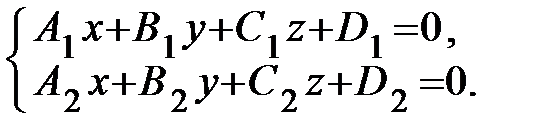 (4.11)
(4.11)
- общие уравнения прямой в простран-
| Рисунок 27 |
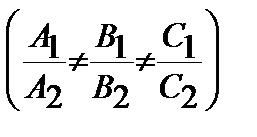 .
.
Пусть прямые l 1 и l 2 заданы своими каноническими уравнениями:
l1: 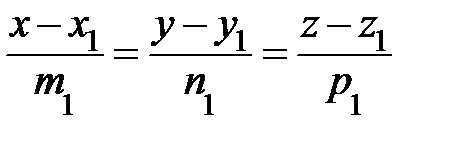 ,
, 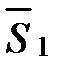 =(=(m1; n1; p1)
=(=(m1; n1; p1)
l2: 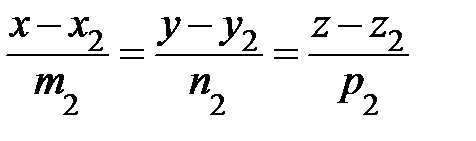 ,
,  =(m2; n2; p2)
=(m2; n2; p2)
Углом φ между прямыми l 1 и l 2 называется наименьший из двух смежных углов, который образуют прямые, проведённые параллельно данным через какую-либо точку пространства.
| x |
| y |
| z |
| S |
| S |
| j |
| l |
| l |
Очевидно, что угол φ можно определить
как угол между направляющими
векторами 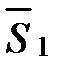 и
и  (рисунок 28).
(рисунок 28).
Рисунок 28
 (4.12)
(4.12)
Если l1 || l2, то направляющие векторы 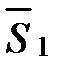 =(m1, n1, p1) и
=(m1, n1, p1) и  =(m2, n2, p2) коллинеарны:
=(m2, n2, p2) коллинеарны:  . (4.13)
. (4.13)
(4.13) - условие параллельности двух прямых l1 и l2
Если l1 ^ l2, то направляющие векторы 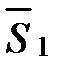 =(m1; n1; p1) и
=(m1; n1; p1) и  =(m2; n2; p2)
=(m2; n2; p2)
взаимно перпендикулярны Þ 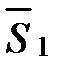 ·
·  = 0 Þ
= 0 Þ
 . (4.14)
. (4.14)
(4.14) - условие перпендикулярности двух прямых l1 и l2.
Прямая и плоскость
Пусть прямая l и плоскость Q заданы уравнениями:
l:  , Q: Ах + Ву + Сz + D= 0
, Q: Ах + Ву + Сz + D= 0
 Углом φ между прямой и плоскостью называется угол между этой прямой и её проекцией на плоскость.
Углом φ между прямой и плоскостью называется угол между этой прямой и её проекцией на плоскость.
Нормаль  =(А; В; С) образует с прямой l угол
=(А; В; С) образует с прямой l угол
(900–φ) (рисунок 29), который можно найти,
если известен направляющий вектор  =(m; n; p).
=(m; n; p).
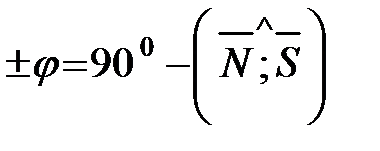 ,
,  Рисунок 29
Рисунок 29
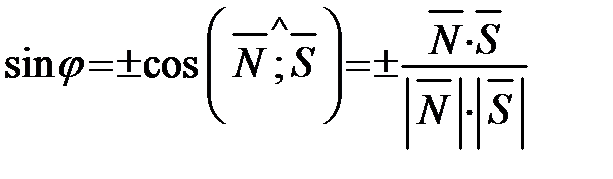 .
.
Для нахождения угла между прямой и плоскостью получаем формулу:
 (4.15)
(4.15)
| N |
| l |
| S |
| Q |
l || Q Þ  =(m; n; p) ^
=(m; n; p) ^  =(А; В; С)
=(А; В; С)
(рисунок 30)Þ  ·
·  = 0.
= 0.
А m + Bn + Cp = 0 (4.16)
условие параллельности прямой и плоскости
Рисунок 30

l ^ Q Þ  ||
||  (рисунок 31)
(рисунок 31)
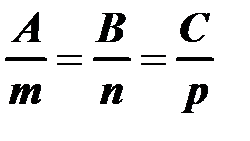 (4.17)
(4.17)
условие перпендикулярности прямой и плоскости
Рисунок 31
Пример 25. Даны координаты точек: А(0; -2; -1), В(2; 4; 0), С(3; 2; 0) и М(-11; 8; 10). Требуется: а) составить уравнение плоскости Q, проходящей через точки А, В, С; б) составить канонические уравнения прямой, проходящей через точку М перпендикулярно плоскости Q.
Решение. а) Воспользуемся уравнением плоскости (4.3), проходящей через три данные точки. Подставив в (4.3) координаты точек А, В и С, получим:
 ;
;  .
.
Разложим определить по элементам первой строки:
 .
.
Сократив на 5 и раскрыв скобки, получим уравнение искомой плоскости Q:
 .
.
| l |
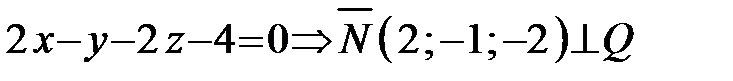 .
.
 Вектор
Вектор  (2; -1; -2) перпендикулярный данной
(2; -1; -2) перпендикулярный данной
плоскости (рисунок 32), будет параллелен искомой
прямой  , т.е. является её направляющим вектором
, т.е. является её направляющим вектором
 . Следовательно, координаты вектора Рисунок 32
. Следовательно, координаты вектора Рисунок 32

 . Итак, для искомой прямой известна точка М(-11; 8; 10), через которую она проходит и направляющий вектор
. Итак, для искомой прямой известна точка М(-11; 8; 10), через которую она проходит и направляющий вектор 
 . Используя канонические уравнение прямой в пространстве (4.8), получаем:
. Используя канонические уравнение прямой в пространстве (4.8), получаем:
 - искомые уравненния.
- искомые уравненния.
Пример 26. Даны координаты точек А(4; 4; -2), В(8; 8; -4), С(-3; -4; 3). Требуется: а) составить канонические уравнения прямой АВ; б) составить уравнение плоскости, проходящей через точку С перпендикулярно прямой АВ, и точку пересечения этой плоскости с прямой АВ.
Решение. а) Воспользуемся уравнениями прямой (4.10), проходящей через две точки, подставляя в них координаты точек А и В:
 ;
;  - канонические уравнения прямой АВ.
- канонические уравнения прямой АВ.
б) Так как по условию задачи плоскость Q перпендикулярна прямой (АВ) (рисунок 33), то в качестве нормального вектора  можно принять направляющий вектор прямой
можно принять направляющий вектор прямой 
 , так как
, так как  перпендикулярен плоскости.
перпендикулярен плоскости.
 Тогда для плоскости известны точка
Тогда для плоскости известны точка  , через которую она проходит, и вектор нормали
, через которую она проходит, и вектор нормали 
 .
.
Следовательно, нужно воспользоваться
уравнением (4.2), подставив в него
соответствующие координаты:
 ;
;
 ; Рисунок 33
; Рисунок 33
 ;
;
 (Q).
(Q).
Чтобы найти точку пересечения прямой (AB) с плоскостью Q, запишем уравнения прямой АВ в параметрическом виде.
Пусть  или
или  ,
,  ;
;  ,
,
где t - некоторый параметр.
Тогда уравнения прямой можно записать в виде (4.9):
х = 4 t + 4; у = 4 t + 4; z = –2 t – 2.
Для нахождения координат точки пересечения прямой и плоскости необходимо решить систему, составленную из их уравнений:
 .
.
Так как координаты х, у, z точки пересечения прямой и плоскости должны удовлетворять уравнениям прямой и уравнению плоскости, то подставляя их значения в данное уравнение плоскости, получим
2(4 t + 4) +2(4 t + 4) – (–2 t - 2) + 17 = 0; 8 t + 8 +8 t + 8 + 2 t + 2 + 17 = 0;
18 t = – 35, откуда  .
.
Найденное значение t есть величина параметра в точке пересечения прямой и плоскости. В результате подстановки этого значения в уравнения прямой в параметрическом виде находим координаты точки пересечения:
 .
.
 .
.
 .
.
Итак, координаты точки Р пересечения данной прямой и плоскости таковы:  .
.