Метод Гаусса заключается в приведении расширенной матрицы системы, (а следовательно, и самой системы) с помощью Э.П. к ступенчатому виду, где все элементы матрицы, стоящие ниже главной диагонали – нули. При этом возможны следующие случаи:
1) Если с помощью Э.П. расширенная матрица системы приведена к треугольному виду:
 , (1.4)
, (1.4)
т.е. ниже главной диагонали – нули, а все элементы главной диагонали нулю не равны, то система имеет единственное решение.
Полученная матрица (1.4) соответствует системе:
 ,
,
в которой последнее уравнение содержит одно неизвестное.
Из такой преобразованной системы все неизвестные определяются без труда, так называемым, обратным ходом.
2) Далее, если в ступенчатом виде расширенной матрицы присутствует хотя бы одна строка вида:
(
 ),
),  где
где 

 ,т.е
,т.е
 , (1.5)
, (1.5)
то система несовместна. Такой строке соответствует уравнение вида
 х1 +
х1 +  х2 + …+
х2 + …+ 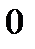 хn =
хn =  , которое не имеет смысла.
, которое не имеет смысла.
3) Если же в ступенчатом виде расширенной матрицы последняя строка, кроме диагонального элемента  , имеет ещё ненулевые элементы, т.е.
, имеет ещё ненулевые элементы, т.е.
 , (1.6)
, (1.6)
то система имеет бесконечное множество решений, т.е. является неопределённой. В этом случае n – k неизвестных объявляются свободными, т.е. принимающими произвольные значения, а остальные k неизвестных выражаются из уравнений системы через них.
Замечание. Для контроля вычислений в расширенную матрицу системы вводится дополнительный (контрольный) столбец, элементы которого равны суммам элементов соответствующей строки расширенной матрицы. При Э.П. строк матрицы такому же преобразованию должны подвергнуться и элементы контрольного столбца. Контролем служит тот факт, что и после проведенного преобразования элементы контрольного столбца вновь равны сумме элементов соответствующей строки. Нарушение этого условия указывает на ошибку в вычислениях.
Пример 1. Решить систему уравнений: 
Решение. Составим расширенную матрицу системы вместе с контрольным столбцом и обозначим каждую строку полученной матрицы буквой  , где i – номер строки:
, где i – номер строки:  .
.
Первый шаг: приведём данную матрицу к треугольному или ступенчатому виду, т.е. к такому, когда для  - первому ненулевому элементу i -ой строки все элементы матрицы, стоящие ниже и левее
- первому ненулевому элементу i -ой строки все элементы матрицы, стоящие ниже и левее  - нулевые.
- нулевые.
Так как в первой строке  первый элемент
первый элемент  , то с помощью Э.П. добьёмся, чтобы ниже
, то с помощью Э.П. добьёмся, чтобы ниже  (т.е. во 2-ой, 3-ей и 4-ой строках) в первом столбце стояли нули. Для этого все элементы
(т.е. во 2-ой, 3-ей и 4-ой строках) в первом столбце стояли нули. Для этого все элементы  умножим на (-2) и сложим с
умножим на (-2) и сложим с  , затем умножим на (-1) и (-3) и сложим соответственно с элементами
, затем умножим на (-1) и (-3) и сложим соответственно с элементами  и
и  . Тогда получим:
. Тогда получим:


При Э.П. этим же преобразованиям подвергаются и элементы контрольного столбца, а затем вновь, суммируя элементы строки матрицы (А|В), сравнивают сумму с соответствующим элементом контрольного столбца. Если эти числа совпали, то арифметические преобразования выполнены верны, если – нет, то необходимо найти ошибки в вычислениях.
Второй шаг: теперь необходимо под вторым элементом строки  получить в строках
получить в строках  и
и  нули. На первом шаге метода Гаусса роль такого элемента выполняла единица, что было удобно при вычислениях. Поэтому поменяем местами
нули. На первом шаге метода Гаусса роль такого элемента выполняла единица, что было удобно при вычислениях. Поэтому поменяем местами  и
и  , одновременно умножив
, одновременно умножив  на (-1), т.е.
на (-1), т.е.  .
.


На третьем шаге метода Гаусса добьёмся, чтобы в строке  первый, отличный от нуля, элемент был единицей. Для этого умножим строку
первый, отличный от нуля, элемент был единицей. Для этого умножим строку  на (-1) и прибавим к третьей, а затем, умножая
на (-1) и прибавим к третьей, а затем, умножая  на (-4) сложим с
на (-4) сложим с  :
:


 .
.
Получена треугольная матрица, т.к. по главной диагонали стоят числа, отличные от нуля (единицы), а ниже неё – нули.
Следовательно, данная система уравнений имеет единственное решение. Для его нахождения выпишем по полученной матрице соответствующую систему уравнений:  . Из последнего уравнения имеем, что
. Из последнего уравнения имеем, что  . Подставляя это значение в предыдущее уравнение, найдём
. Подставляя это значение в предыдущее уравнение, найдём  или
или  . Из второго уравнения определяем
. Из второго уравнения определяем 
или  , а из первого уравнения находим
, а из первого уравнения находим  или
или  .
.
Таким образом, система уравнений имеет единственное решение (1; 2; 3; 4).
Пример 2. Решить систему уравней: 
Решение. Выпишем расширенную матрицу системы вместе с контрольным столбцом и с помощью шагов метода Гаусса приведём её к ступенчатому виду:





 .
.
Получена ступенчатая матрица, для которой запишем соответствующую систему уравнений:  . Так как эта система после исключения неизвестных приведена к ступенчатому виду, в котором число неизвестных
. Так как эта система после исключения неизвестных приведена к ступенчатому виду, в котором число неизвестных
n = 3 больше числа уравнений k = 2, из которых их надо определить, то система неопределённа, то есть имеет бесчисленное множество решений.
Для его нахождения определяем число свободных неизвестных: 
 . Следовательно, одно из неизвестных можно считать свободным, т.е. принимающим произвольные значения. В качестве него лучше выбирать то неизвестное, которое входит сразу во все уравнения получившейся системы. Таковыми в данном примере являются
. Следовательно, одно из неизвестных можно считать свободным, т.е. принимающим произвольные значения. В качестве него лучше выбирать то неизвестное, которое входит сразу во все уравнения получившейся системы. Таковыми в данном примере являются  и
и  . Выберем в качестве свободного неизвестного
. Выберем в качестве свободного неизвестного  . Тогда из второго уравнения выражаем
. Тогда из второго уравнения выражаем  через
через  :
:  . Подставляя полученную связь между
. Подставляя полученную связь между  и
и  в первое уравнение, найдём зависимость
в первое уравнение, найдём зависимость  от
от  :
:  или
или  .
.
Откуда окончательно имеем:  .
.
Таким образом, система имеет бесчисленное множество решений:  ;
;  ;
;  .
.
Пример 3. Решить систему уравнений  .
.
Решение.




 .
.
Так как последней строке полученной матрицы соответствует уравнение  , которое является противоречивым, то система несовместна.
, которое является противоречивым, то система несовместна.