Определение. Функция α(х) называется бесконечно малой в точке  , если
, если
её предел в этой точке равен нулю, т. е.  .
.
Определение. Функция β(х) называется бесконечно большой при 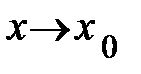
если 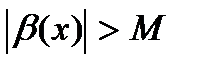 при
при 
где М – произвольное положительное число.
Запись: 
Если ввести обозначения: «бесконечно малая» –0 (х), «бесконечно большая» - 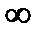 , с – число, f(х) – ограниченная функция, тогда можно перечислить основные свойства бесконечно малых и бесконечно больших:
, с – число, f(х) – ограниченная функция, тогда можно перечислить основные свойства бесконечно малых и бесконечно больших:
| 0(х) ± 0(х) = 0(х) | ∞ + ∞ = ∞ |
| f(х) · 0(х) = 0(х) | f(х) · ∞ = ∞ 
|
| 0(х) · 0(х) = 0(х) | ∞ · ∞ = ∞ |
| С · 0(х) = 0(х) | С· ∞ = ∞ |
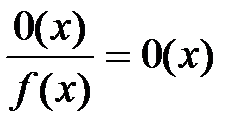 , , 
| 
|

| 
|
Пример 28. Найти  .
.
Решение. В этом случае теорему о пределе частного применить нельзя, т.к. предел знаменателя равен нулю. Таким образом, в знаменателе бесконечно малая. Тогда величина  - есть бесконечно большая, как величина,
- есть бесконечно большая, как величина,
обратная бесконечно малой. Поэтому 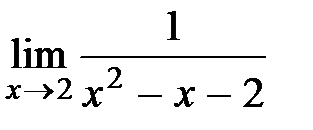 =
=  .
.
Заметим, что среди перечисленных свойств бесконечно малых и больших нет соотношений вида 
Такие соотношения называют неопределённостями в силу того, что предел каждого из перечисленных соотношений в зависимости от конкретного задания функций может быть конечным, бесконечным, а может и не существовать. Отыскание таких пределов называется раскрытием неопределённостей.
Пример 29. Найти  .
.
Решение. Непосредственная подстановка в данное выражение предельного значения аргумента х = 1 приводит к неопределённому выражению  , так в числителе: 13 - 1 =0, в знаменателе: 12 – 4 + 3 = 0.
, так в числителе: 13 - 1 =0, в знаменателе: 12 – 4 + 3 = 0.
Следовательно, прежде чем перейти к пределу, необходимо данное выражение преобразовать. Разложим числитель и знаменатель на множители, используя формулы:
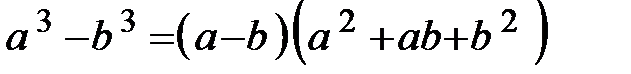 ;
;  ,
,
где 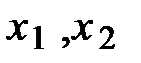 - корни квадратного трехчлена, определяемые по формуле
- корни квадратного трехчлена, определяемые по формуле 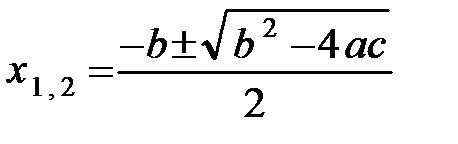 . Тогда
. Тогда

 =
=  =
= 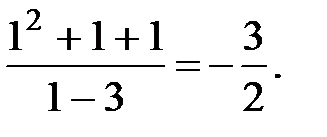
Пример 30. Найти 
Решение. Здесь также имеем неопределённость вида  ; чтобы её раскрыть, умножим числитель и знаменатель на выражение, сопряжённое числителю; после этого можно будет сократить на х2 и тем самым убрать неопределённость:
; чтобы её раскрыть, умножим числитель и знаменатель на выражение, сопряжённое числителю; после этого можно будет сократить на х2 и тем самым убрать неопределённость: 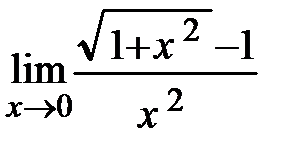
 =
=
= 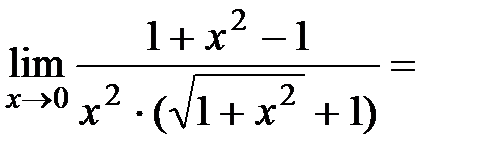

 =
=  =
= 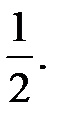
Пример 31. Найти  .
.
 Решение. При х ® ¥ числитель и знаменатель дроби неограниченно возрастают. В таком случае говорят, что имеет место неопределённость вида
Решение. При х ® ¥ числитель и знаменатель дроби неограниченно возрастают. В таком случае говорят, что имеет место неопределённость вида  . Так как рост многочленов обуславливают их старшие степени, то в подобного рода примерах в числителе и в знаменателе дроби оставляют слагаемые, содержащие старшие степени вместе с их коэффициентами. Затем поделив степени, переходят к пределу:
. Так как рост многочленов обуславливают их старшие степени, то в подобного рода примерах в числителе и в знаменателе дроби оставляют слагаемые, содержащие старшие степени вместе с их коэффициентами. Затем поделив степени, переходят к пределу:

 =
=  =
=  = 0.
= 0.
Пример 32. Найти 
 Решение. Вычислим этот предел, используя сформулированное выше правило, причём, для того, чтобы определить в числителе слагаемое, содержащее старшую степень переменной, достаточно перемножить старшие степени каждой скобки. Таким образом имеем:
Решение. Вычислим этот предел, используя сформулированное выше правило, причём, для того, чтобы определить в числителе слагаемое, содержащее старшую степень переменной, достаточно перемножить старшие степени каждой скобки. Таким образом имеем:

 =
= 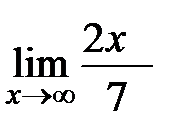 =
= 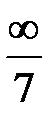 = ∞.
= ∞.
Специальные пределы
Если при вычислении предела получена неопределённость вида  , а в функции, стоящей под знаком предела встречаются тригонометрические и (или) обратные тригонометрические функции, то при вычислении таких пределов часто используется формула:
, а в функции, стоящей под знаком предела встречаются тригонометрические и (или) обратные тригонометрические функции, то при вычислении таких пределов часто используется формула:  , (5.1)
, (5.1)
которая называется первым специальным (замечательным) пределом, а также следствия из неё:  ; (5.2)
; (5.2)
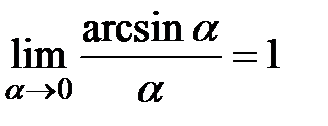 ; (5.3)
; (5.3)  . (5.4)
. (5.4)
Второй специальный предел
 (5.5) или
(5.5) или  (5.6)
(5.6)
раскрывает неопределённость вида 1∞, где  - число Непера.
- число Непера.
Пример 33. Найти 
Решение. При х → 0 α = 5х также стремится к нулю, поэтому, умножая числитель и знаменатель данной дроби на 5 и применяя формулу (5.1), получим 
 = 5
= 5  = 5 · 1 = 5.
= 5 · 1 = 5.
Пример 34. Найти 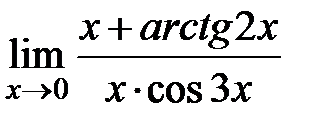 .
.
Решение. При подстановке предельного значения переменной (т.е. х=0)
убеждаемся, что имеем неопределённость вида 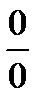 . Разделив числитель и знаменатель данной дроби на х и используя свойства пределов и формулу (5.4), получим:
. Разделив числитель и знаменатель данной дроби на х и используя свойства пределов и формулу (5.4), получим:
 =
=  =
=  =
= 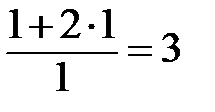
Пример 35. Найти  .
.
| =1 |
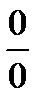 . Для её раскрытия используем следствия из первого специального предела:
. Для её раскрытия используем следствия из первого специального предела:
| =1 |
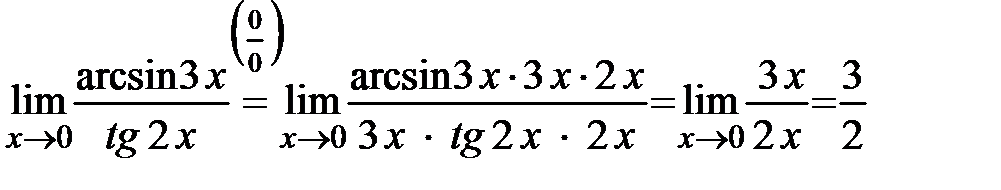 .
.
Пример 36. Найти  .
.
Решение. При  данная функция представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности (неопределённость вида
данная функция представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности (неопределённость вида  ). Для того, чтобы раскрыть эту неопределённость, представляем основание в виде 1 + α, а в показателе выделяем множитель
). Для того, чтобы раскрыть эту неопределённость, представляем основание в виде 1 + α, а в показателе выделяем множитель  , обратный
, обратный  :
:

переходя к пределу в квадратной скобке, получим число  , согласно
, согласно
формуле (5.6), а в показателе раскрываем неопределённость 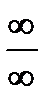 :
:

 .
.