Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объём производства каждой из п отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а сдругой – как потребитель продукции и своей, и произведённой, другими отраслями.
Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В.Леонтьевым
Предположим, что рассматривается п отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени (например, год).
Введём следующие обозначения: хi - общий (валовой) объём продукции i - й отрасли (i = 1,2,..., n);
xij – объём продукции i - й отрасли, потребляемой j -й отраслью в процессе производства (i, j = 1,2,..., n);
уi – объём конечного продукта i - й отрасли для непроизводственного потребления.
Так как валовой объём продукции любой i - й отрасли равен суммарному объёму продукции, потребляемой п отраслями, и конечного продукта, то
 (1.15)
(1.15)
Уравнения (1.15) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (1.15), имеют стоимостное выражение.
Введём коэффициенты прямых затрат  :
:
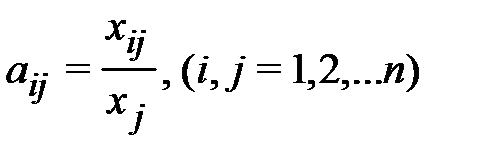 (1.16)
(1.16)
показывающие затраты продукции i -й отрасли на производство единицы продукции j -й отрасли.
Можно полагать, что в некотором промежутке времени коэффициенты aij будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
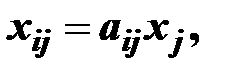
 (1.17)
(1.17)
вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной. Теперь соотношения баланса (1.15) примут вид:
 (1.18)
(1.18)
Обозначим 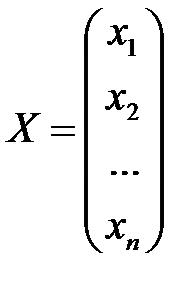 ,
, 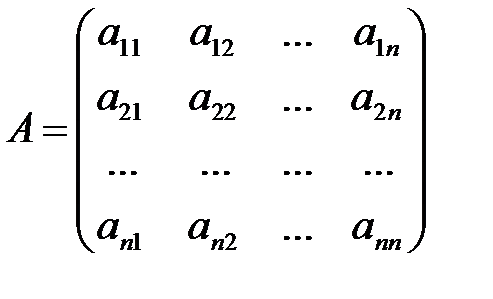 ,
,  ,
,
где Х – вектор валового выпуска, Y – вектор конечного продукта,А – матрица прямых затрат (технологическая или структурная матрица).
Тогда систему (1.15) можно записать в матричном виде:
X = AX + Y. (1.19)
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.
Перепишем уравнение (1.19) в виде:
(E – A) X =Y (1.20)
Если матрица (Е – А) невырожденная, т.е. |Е – А |≠0, то
X = (E – A)-1 Y. (1.21)
Матрица S = (Е – А)-1 называется матрицей полных затрат.
Каждый элемент sij матрицы S есть величина валового выпуска продукции i -й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j -й отрасли  (j =1,2,..., n).
(j =1,2,..., n).
В соответствии с экономическим смыслом задачи значения хi должны быть неотрицательны при неотрицательных значениях
 и
и  , где i, j = 1, 2,…, n.
, где i, j = 1, 2,…, n.
Определение. Матрица А ≥ 0 называется продуктивной, если для любого вектора Y ≥ 0 существует решение X ≥ 0 уравнения (Е-А)Х=Y. В этом случае и модель Леонтьева называется продуктивной.
Существует несколько критериев продуктивности матрицы А.
Первый критерий продуктивности. Матрица А продуктивна, если максимум сумм элементов её столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица А продуктивна, если  для любых i, j = 1,2,..., n и
для любых i, j = 1,2,..., n и  , и существует номер j такой, что
, и существует номер j такой, что  .
.
Второй критерий продуктивности. Матрица A ≥ 0 продуктивна тогда и только тогда, когда матрица (Е – А) – 1 существует и неотрицательна.
Пример 9. В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.:
| Отрасль | Потребление | Конеч-ный продукт | Валовой выпуск | ||
| энергетика | машиностроение | ||||
| Производство | Энергетика Машиностроение | ||||
Вычислить необходимый объём валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроение сохранится на прежнем уровне.
Решение. Имеем 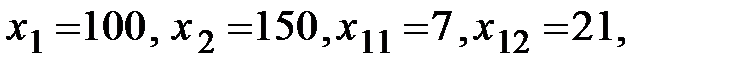
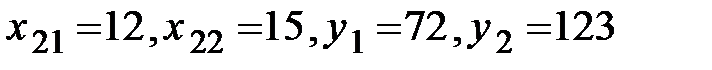 .
.
По формуле (1.16) находим коэффициенты прямых затрат: 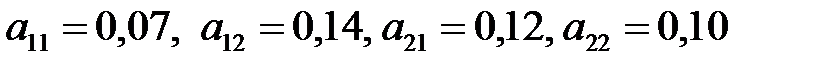 , т.е матрица прямых затрат
, т.е матрица прямых затрат
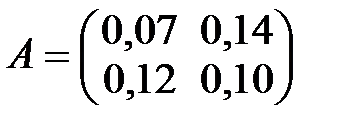 имеет неотрицательные элементы и удовлетворяет первому критерию продуктивности:
имеет неотрицательные элементы и удовлетворяет первому критерию продуктивности:  .
.
Поэтому для любого вектора конечного продукта Y можно найти необходимый объём валового выпуска Х по формуле (1.21):
X = (E – A)-1 ×Y
Найдём матрицу полных затрат S = (E – A)-1:
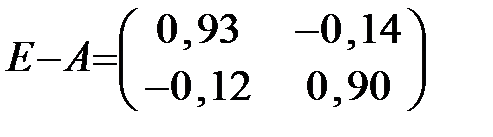 . Так как | Е – А |=0,8202 ≠ 0, то по формуле (1.14) для вычисления обратной матрицы имеем:
. Так как | Е – А |=0,8202 ≠ 0, то по формуле (1.14) для вычисления обратной матрицы имеем: 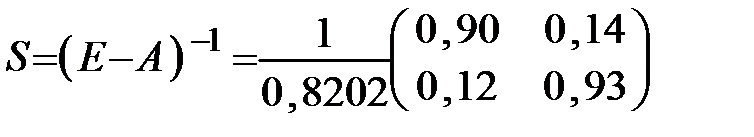 .
.
По условию вектор конечного продукта должен быть равен 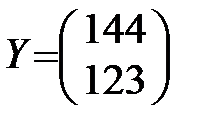 . Тогда по формуле (1.21) получаем вектор валового выпуска:
. Тогда по формуле (1.21) получаем вектор валового выпуска:
 , т.е. валовой выпуск в энергетической отрасли надо увеличить до 179, 0 усл. ед., а в машиностроительной – до 160,5 усл. ед.
, т.е. валовой выпуск в энергетической отрасли надо увеличить до 179, 0 усл. ед., а в машиностроительной – до 160,5 усл. ед.
Ответ:  (усл. ед.),
(усл. ед.),  (усл. ед.).
(усл. ед.).
Векторная алгебра
Основные понятия векторной алгебры
Определение. Вектором называется направленный отрезок АВ, в котором
точка А рассматривается как начало, а точка В – как конец.
Вектор обозначается  или
или  , и изображается следующим образом:
, и изображается следующим образом:
В Модуль (длина) вектора обозначается  или
или 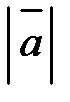 .
.
А или 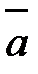
Определение. Векторы называются коллинеарными, если они расположены
на одной или на параллельных прямых, и компланарными,
если они лежат на одной или на параллельных плоскостях.
Определение. Векторы называются равными, если: а) равны их длины;
б) они коллинеарны; с) направлены в одну сторону.
Определение. Координатами 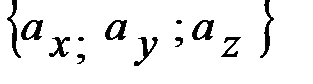 вектора
вектора  в системе ХОУ
в системе ХОУ
называются проекции этого вектора на оси Ох, Оу, Оz.
В этом случае пишут: 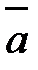 =
= 
Определение. Базисными ортами называются единичные векторы 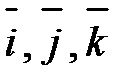 , направленные соответственно по координатным осям Ох, Оу, Оz.
, направленные соответственно по координатным осям Ох, Оу, Оz.
Координаты вектора являются коэффициентами его разложения по ортам:

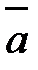 = ах ·
= ах ·  + ау ·
+ ау · 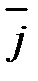 + аz ·
+ аz · 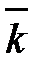 . (2.1)
. (2.1)
Если известны координаты точек А(х1; у1; z1) и В(х2; у2; z2), то
координаты вектора  равны разностям соответсвующих координат его
равны разностям соответсвующих координат его
конца В и начала А, т.е.

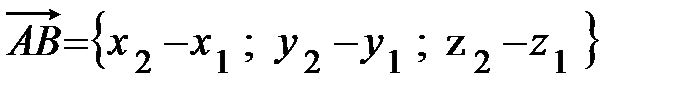 . (2.2)
. (2.2)
Длина вектора, заданного своими координатами 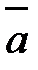 =
=  , вычисляется по формуле:
, вычисляется по формуле:
 . (2.3)
. (2.3)
При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются), а при умножении вектора на число каждая его координата умножается на это число.
Пример 10. Вектор  задан координатами начала А и конца В: А (-2;3;-5),
задан координатами начала А и конца В: А (-2;3;-5),
В (2; -3; 1). Найти координаты вектора и его длину.
Решение. По формуле (2.2) найдём координаты вектора  :
:  = {4; -6; 6}
= {4; -6; 6}
По формуле (2.3) определяем его длину:  .
.
Ответ:  =
= 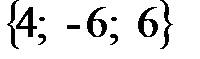 ;
; 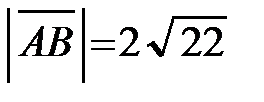 .
.
Пример 11. Даны три вектора: 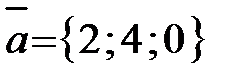 ,
, 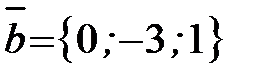 ,
,  .
.
Найти координаты вектора 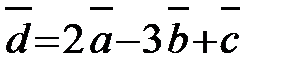 .
.
Решение. Имеем  ,
,  ,
,  .
.
Тогда 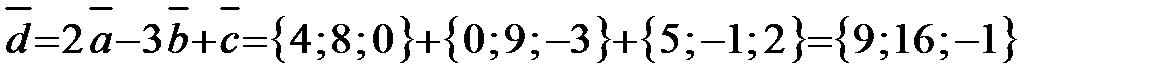 .
.
Ответ:  .
.